Правила балльной оценки контрольной работы

Стр 1 из 2Следующая ⇒

МЕТОДИЧЕСКОЕ РУКОВОДСТВО

ПО ОРГАНИЗАЦИИ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ

ЧАСТЬ 2

Учебная дисциплина ЭКОНОМЕТРИКА

Для студентов направления 080100 «Экономика»

профилей «Финансы и кредит»

«Налоги и налогообложение»

«Бухгалтерский учет, анализ и аудит»

Новосибирск 2011

Методическое руководство разработано

Пашкевич Мариной Геннадьевной – доцентом кафедры высшей математики,

Пудовой Мариной Владимировной – доцентом кафедры высшей математики

Учебно-методическое обеспечение согласовано с библиотекой университета.

Зав.библиотекой Н.Ю.Долгова

Методическое руководство по организации самостоятельной работы студентов соответствует внутреннему стандарту НГУЭУ

Начальник отдела по планированию

и организации учебно-методической

работы В.Е. Федорова

Утверждено на заседании кафедры высшей математики

(протокол от «25» августа 2011 г. № 1).

Заведующий кафедрой

к.ф.-м. н., доцент Ю.Н. Владимиров

Ó Новосибирский государственный университет экономики и управления «НИНХ»

РАЗДЕЛ 1. ОБЩИЕ ПОЛОЖЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ

Целью изучения дисциплины «Эконометрика» является ознакомление с методами количественного выражения взаимосвязей экономических процессов и явлений и освоение методов анализа информации и прогнозирования развития бизнес-процессов.

Выполнение контрольной работы студентами нацелено на развитие знаний и навыков в части вопросов, касающихся раскрытия финансов как разносторонней объективной экономической категории, присущей современным системам хозяйствования и широко используемой государством для повышения эффективности общественного производства.

Задачи, решаемые в ходе выполнения контрольной работы состоят в том, чтобы в результате знакомства с разделами, предусмотренными данной дисциплиной студент(ка) должен:

· иметь представление о существующих подходах к изучению эконометрических моделей и задачах, решаемых эконометрическими методами;

· знать основные понятия эконометрического анализа и методы количественной оценки социально-экономических процессов;

· уметь применять современные компьютерные технологий в экономико-математическом моделировании, самостоятельно решать задачи регрессионного анализа и интерпретировать полученные результаты.

К итоговой форме контроля по дисциплине студент(ка) допускаются при наличии зачета по контрольной работе .

Оформление контрольной работы:

В печатном варианте контрольная оформляется на листах А4 (210х297мм), WORD, Times New Roman 14, интервал 1,5. Поля: верхнее, левое, нижнее – 20 мм, правое – 10 мм.

При рукописном варианте – на листах формата А4 или на тетрадных листах, заполняемых с обеих сторон разборчивым почерком.

РАЗДЕЛ 2. ИНСТРУКЦИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

2.1. Этапы написания контрольной работы:

1.Внимательно и вдумчиво изучить данные Методические указания, получив при необходимости на кафедре ответы на возникшие вопросы (консультацию).

2.Безошибочно определить свой вариант контрольной работы согласно правилам, в противном случае работа к защите не допускается.

3.Ситуационные (практические) задачи для своего решения требуют знания теоретического материала (см. список рекомендуемой литературы). Следует внимательно ознакомиться с условиями задач и определить, на какую из тем курса «Эконометрика» приходится задача, и затем использовать соответствующую методику расчёта или принцип для её решения.

4. Успешные ответы на вопросы тестового задания требуют знания основных понятий, определений, формулировок, терминологии и основных положений из области эконометрического моделирования.

5. Оформить титульный лист в соответствии со стандартом:

Федеральное агентство по образованию Новосибирский государственный университет экономики и управления – «НИНХ» Номер группы: Специальность: Студент (ФИО) Номер зачётной книжки: Кафедра Высшей математики Учебная дисциплина: Математика

Номер варианта работы: ____ Дата регистрации на кафедре: «___» ________ 20 г. Проверил: ФИО преподавателя (Год) 20_

6.Выполнить текст контрольной работы в полном соответствии с содержанием и структурой, согласно пункту 2.3.

2.2. Правила выбора варианта работы

Студент(ка) осуществляет выбор по следующему правилу: в таблице 2.2.1 по строке смотрит для последней цифры номера своей зачетной книжки (например 9) номер варианта контрольной работы: № 9, который и следует выполнить.

2.2.1. Таблица выбора варианта контрольной работы

Последняя цифра № зачётной книжки	Номер вариантаконтрольной работы
	№ 1
	№ 2
	№ 3
	№ 4
	№ 5
	№ 6
	№ 7
	№ 8
	№ 9
	№ 10

Внимание!Контрольные работы,выполненныене по своему варианту,к проверке и защитене допускаются.

2.3. Структура контрольной работы

Содержание работы выполняется в соответствии со следующей структурой:

1. Ситуационная (практическая) часть:

1.1. Текст ситуационной (практической) задачи № 1;

1.2. Решение задачи № 1;

1.3. Ответ на задачу №1

1.4. Текст ситуационной (практической) задачи № 2;

1.5. Решение задачи № 2;

1.6. Ответ на практическую задачу № 2.

2. Тестовая часть:

2.1. Содержание 10 (десяти) тестовых заданий варианта (тексты вопросов) и ответ на каждое из заданий.

3. Библиографический список.

РАЗДЕЛ 3. ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

Вариант № 1.

Ситуационная (практическая) задача № 1

По 20 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x₁(% от стоимости фондов на конец года) и от ввода в действие новых основных фондов x2(%).

Номер предприятия	y	X1	X2	Номер предприятия	y	X1	X2
			3,5				6,3
			3,6				6,4
			3,9
			4,1				7,5
			4,2				7,9
			4,5				8,2
			5,3				8,4
			5,3				8,6
			5,6				9,5

Требуется:

1.Построить корреляционное поле между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации. Выдвинуть гипотезу о тесноте и виде зависимости между показателями X1 и Y.

2. Оценить тесноту линейной связи между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации с надежностью 0,9.

3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости выработки продукции на одного работника от удельного веса рабочих высокой квалификации.

4. Проверить статистическую значимость параметров уравнения регрессии с надежностью 0,9 и построить для них доверительные интервалы.

5. Рассчитать коэффициент детерминации. С помощью F -критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью 0,9.

6. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих.

7.Рассчитать коэффициенты линейного уравнения множественной регрессии и пояснить экономический смысл его параметров.

8. Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,9 и построить для них доверительные интервалы.

9.Найти коэффициенты парной и частной корреляции. Проанализировать их.

10.Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.

11.С помощью F -критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,9.

12. Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих, а ввод в действие новых основных фондов составляет 5%.

13. Проверить построенное уравнение на наличие мультиколлинеарности по: критерию Стьюдента; критерию χ2. Сравнить полученные результаты.

Ситуационная (практическая) задача № 2

Имеются помесячные данные по объему платных услуг населению в 2010 г.

месяц	Объем платных услуг, млн. руб.	месяц	Объем платных услуг, млн. руб.
январь	29,08	июль	38,53
февраль	32,13	август	41,57
март	32,65	сентябрь	44,56
апрель	35,43	октябрь	55,98
май	35,1	ноябрь	62,45
июнь	39,31	декабрь	65,12

Требуется:

1. Проверить гипотезу о наличии тренда во временном ряде.

2. Рассчитать коэффициенты автокорреляции. Проверить наличие сезонных колебаний во временном ряде.

3. Оценить параметры линейной трендовой модели, проверить статистическую значимость соответствующего уравнения регрессии с надежностью 0,99.

4. Дать точечный и интервальный прогноз объема платных услуг на февраль 2011 г. с надежностью 0,99.

Тестовые задания

Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению.

1.Остаток в i-м наблюдении – это:

a) разница между значением объясняющей переменной в i-м наблюдении и прогнозным значением этой переменной;

b) разница между значением переменной Y в i-м наблюдении и прогнозным значением этой переменной, полученным по выборочной линии регрессии;

c) разница между значением переменной Y в i-м наблюдении и прогнозным

значением этой переменной, полученным по истинной линии регрессии;

d) разница между прогнозным значением зависимой переменной, полученным

по выборочной линии регрессии и значением объясняющей переменной в

этом наблюдении.

2. Дано регрессионное уравнение Y = 10+ 0.5X. Чему равно прогнозное значение переменной Y, если Х = 10:

a) 20;

b) 15;

c) 5;

d) 0.

3. При анализе тесноты линейной корреляционной связи между двумя

переменными получен коэффициент парной линейной корреляции, равный

–1. Это означает, что:

a) линейная корреляционная связь отсутствует;

b) между переменными существует нелинейная связь;

c) парный коэффициент корреляции не может принять такое значение;

d) между переменными существует точная обратная линейная зависимость;

4. С помощью какой меры невозможно избавиться от мультиколлинеарности?
a) увеличение объема выборки;
b) исключения переменных высококоррелированных с остальными;
c) изменение спецификации модели;
d) преобразование случайной составляющей.

5. Какое из приведенных чисел может быть значением коэффициента множественной детерминации:
а) 0,4;
б) -1;
в) -2,7;
г) 2,7.

6. Если значение статистики Дарбина-Уотсона равно 0, это говорит

а) о наличии положительной автокорреляции остатков в модели;
б) об отсутствии зависимости между рассматриваемыми показателями;
в) об отсутствии тренда во временном ряде;
г) о статистической незначимости коэффициентов уравнения.

7. К каким последствиям приводит наличие гетероскедастичности в остатках:

a) МНК-оценки коэффициентов уже не обладают меньшей дисперсией, но

остаются несмещенными и линейными;

b) МНК-оценки коэффициентов остаются наилучшими линейными

несмещенными оценками, проблема только в стандартных ошибках, их надо

корректировать.

c) МНК-оценки коэффициентов уже не обладают меньшей дисперсией, но

остаются несмещенными и линейными; МНК – стандартные ошибки

правильны (состоятельны), тестами, в которых они участвуют, пользоваться

можно.

d) МНК-оценки коэффициентов становятся нелинейными.

8. Периодические колебания, возникающие под влиянием смены времени года называются…
a) хронологическими;
b) сезонными;
c) тенденцией;
d) случайными.

9. Известны помесячные данные за полгода относительно прибыли некоторой компании (тыс. руб.): 100, 110, 98, 90, 100, 110. Медиана данного ряда равна

a) 100;

b) 94;

c) 110;

d) 90.

10. В чем состоит проблема идентификации модели?
a) получение однозначно определенных параметров модели, заданной системой одновременных уравнений;
b) выбор и реализация методов статистического оценивания неизвестных параметров модели по исходным статистическим данным;
c) проверка адекватности модели;

d) выбор общего вида модели.

Вариант № 2.

Ситуационная (практическая) задача № 1

Изучается влияние стоимости основных и оборотных средств на величину валового дохода торговых предприятий. Для этого по 16 торговым предприятиям были получены данные, приведенные в таблице.

№ пред-приятия	Валовой доход за год, y, млн.руб.	Среднегодовая стоимость, млн. руб.	№ пред-приятия	Валовой доход за год, y, млн.руб. основных фондов	Среднегодовая стоимость, млн. руб.
основных фондов	оборотных средств	основных фондов	оборотных средств

Требуется:

1.Построить корреляционное поле между валовым доходом и стоимостью оборотных средств. Выдвинуть гипотезу о тесноте и виде зависимости между этими показателями.

2. Оценить тесноту линейной связи между валовым доходом и стоимостью оборотных средств с надежностью 0,99.

3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости валового дохода от стоимости оборотных средств.

4. Проверить статистическую значимость параметров уравнения регрессии с надежностью 0,95 и построить для них доверительные интервалы.

5. Рассчитать коэффициент детерминации. С помощью F -критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью 0,99.

6. Дать точечный и интервальный прогноз с надежностью 0,99 величины валового дохода для предприятия с оборотом 100 млн. руб.

8. Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,99 и построить для них доверительные интервалы.

9. Найти коэффициенты парной и частной корреляции. Проанализировать их.

10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.

11.С помощью F -критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,99.

12. Дать точечный и интервальный прогноз с надежностью 0,99 величины валового дохода для предприятия, на котором стоимость основных фондов составляет 70 млн. руб., а стоимость оборотных средств - 100 млн. руб.

Ситуационная (практическая) задача № 2

Динамика выпуска продукции за 1994-2008 гг. представлена в таблице.

Год	Выпуск , ед	Год	Выпуск, ед	Год	Выпуск, ед

Требуется:

1. Проверить гипотезу о наличии тренда во временном ряде.

2. Рассчитать коэффициенты автокорреляции. Проверить наличие сезонных колебаний во временном ряде.

3. Оценить параметры линейной трендовой модели, проверить статистическую значимость соответствующего уравнения регрессии с надежностью 0,95.

4. Дать точечный и интервальный прогноз выпуска продукции на 2009 г. с надежностью 0,95.

Тестовые задания

Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению.

1. Ошибка в i-м наблюдении – это:

a) разница между значением объясняющей переменной в i-м наблюдении и

прогнозным значением этой переменной;

b) разница между значением переменной Y в i-м наблюдении и прогнозным

значением этой переменной, полученным по выборочной линии регрессии;

c) разница между значением переменной Y в i-м наблюдении и прогнозным

значением этой переменной, полученным по истинной линии регрессии;

d) разница между прогнозным значением зависимой переменной, полученным

по выборочной линии регрессии и значением объясняющей переменной в

этом наблюдении.

2. Анализ тесноты и направления связей двух признаков осуществляется на основе:
a) парного коэффициента корреляции;
b) коэффициента детерминации;
c) множественного коэффициента корреляции;

d) нормированного коэффициента детерминации.

3. По результатам наблюдений получено следующее регрессионное уравнение

Y* = 0.75 + 0.350 X1 + 2X2 − 0.128 X3, где

Y - цена квартиры в тыс. дол., X1 - общая площадь в кв. м., X2 - первый или последний этаж (1-нет, 0-да), X3 - расстояние от Центра, км.

Как изменится цена на квартиру, если общая площадь увеличится на 1 кв. м. при прочих равных условиях:

a) уменьшится на 350 долл.;

b) в среднем увеличится на 350 долл.;

c) уменьшится на 128 долл.;

d) в среднем увеличится на 2 тыс. долл.

4. Фиктивные переменные могут принимать значения:
a) 1 и 0;
b) 2;
c) -1 и 1;
d) любые значения.

5. Скорректированный коэффициент детерминации

a) всегда растет с увеличением количества объясняющих переменных;
b) не меняется с увеличением количества объясняющих переменных;
c) всегда уменьшается с увеличением количества объясняющих переменных;
d) может уменьшиться с увеличением количества объясняющих переменных.

6. Какой из перечисленных методов не может быть применен для обнаружения гетероскедастичности?
a) Тест Голфелда-Квандта;
b) Тест ранговой корреляции Спирмена;
c) Метод рядов;

d) Тест Дарбина-Уотсона.

7. К каким последствиям приводит наличие автокорреляции остатков:

a) МНК-оценки коэффициентов не будут состоятельными;

b) МНК-оценки коэффициентов не будут несмещенными;.

c) МНК-оценки коэффициентов не будут эффективными;

d) МНК-оценки коэффициентов становятся нелинейными.

8. Аддитивная модель:
a) представляет собой сумму компонент временного ряда;
b) представляет собой произведение компонент временного ряда;
c) представляет собой сумму и произведение соответствующих компонент;

d) представляет собой частное компонент временного ряда.

9. По месячным данным за два года построена трендовая модель, описывающая динамику курса акций некоторой компании: . Каков прогноз курса акций рассматриваемой компании на февраль будущего года?

a) 91;

b) 11,5;

c) 70;

d) 88.

10. Какой метод применяется для оценивания параметров сверхидентифицированного уравнения?
a) МНК;
b) КМНК;
c) ДМНК;

d) ОМНК.

Вариант № 3.

Ситуационная (практическая) задача № 1

Имеются следующие данные о ценах и дивидендах по обыкновенным акциям, а также данные о доходности компании.

№	цена акции, долл. США	доходность капитала, %	уровень дивидендов, %	№	цена акции, долл. США	доходность капитала, %	уровень дивидендов, %
		15,2	2,6			12,7	2,4
		13,9	2,1			15,3	2,6
		15,8	1,5			15,2	2,8
		12,8	3,1			12,0	2,7
		6,9	2,5			15,3	1,9
		14,6	3,1			13,7	1,9
		15,4	2,9			13,3	1,6
		17,3	2,8			15,1	2,4
		13,7	2,4			15,0	3,0

Требуется:

1.Построить корреляционное поле между ценой акции и уровнем дивидендов. Выдвинуть гипотезу о тесноте и виде зависимости между уровнем дивидендов и ценой.

2. Оценить тесноту линейной связи между ценой акции и уровнем дивидендов с надежностью 0,95.

3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости цены акции от уровня дивидендов.

5. Рассчитать коэффициент детерминации. С помощью F -критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью 0,95.

6. Дать точечный и интервальный прогноз с надежностью 0,95 цены акции, если дивиденды составляют 2,2%.

8. Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,95 и построить для них доверительные интервалы.

9. Найти коэффициенты парной и частной корреляции. Проанализировать их.

10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.

11.С помощью F -критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,95.

12. Дать точечный и интервальный прогноз с надежностью 0,95 величины цены акции компании с доходностью капитала 17% и уровнем дивидендов 2,2%.

Ситуационная (практическая) задача № 2

Имеются поквартальные данные за последние 6 лет об объеме экспорта в России (100 млрд. долл.).

№ кв-ла	Экспорт	№ кв-ла	Экспорт	№ кв-ла	Экспорт
	51,47		61,06		72,44
	54,69		60,44		73,42
	53,39		59,14		74,36
	56,61		57,22		75,34
	55,31		68,6		76,28
	58,53		69,58		77,26
	64,28		70,52		78,2
	62,36		71,5		79,18

Требуется:

1. Проверить гипотезу о наличии тренда во временном ряде.

2. Рассчитать коэффициенты автокорреляции. Проверить наличие сезонных колебаний во временном ряде.

3. Оценить параметры линейной трендовой модели, проверить статистическую значимость соответствующего уравнения регрессии с надежностью 0,9.

4. Дать точечный и интервальный прогноз объема экспорта на первый квартал следующего года с надежностью 0,9.

Тестовые задания

Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению.

1. Укажите неверное утверждение относительно метода наименьших квадратов

(МНК) оценки линейной регрессионной модели:

a) МНК минимизирует сумму квадратов остатков;

b) МНК стоит линию регрессии, проходящую через «центр поля рассеяния»;

c) МНК максимизирует сумму квадратов остатков;

d) МНК строит линию регрессии, которая близка одновременно ко всем точкам

поля рассеяния.

2. Какое из приведенных чисел может быть значением парного коэффициента корреляции:
a) 0,1;
b) 1,5;
c) -2,7;
d) 4.

3. По 16 наблюдениям построено парное линейное уравнение регрессии. Для проверки значимости коэффициента регрессии вычислено t_набл=2,5.
а) Коэффициент незначим при α=0,05;
б) Коэффициент значим при α =0,05;
в) Коэффициент значим при α =0,01;

d) Коэффициент незначим при α =0,1.

4. В каких пределах меняется частный коэффициент корреляции?
a) от -∞ до +∞;
b) от 0 до 1;
c) от 0 до +∞;
d) от –1 до +1.

5. Укажите верное утверждение:

a) если R² =1, то F = 1;
b) коэффициент детерминации всегда растет при увеличении количества объясняющих переменных;
c) выбор вида уравнения множественной регрессии можно осуществить путем графического анализа выборочных данных;
d) Множественный индекс корреляции I и коэффициент детерминации R²связаны соотношением I = 1-R².

6. Если статистика Дарбина-Уотсона равна 2, это говорит

a) об отсутствии автокорреляции остатков;

b) о наличии положительной автокорреляции остатков;

c) о наличии отрицательной автокорреляции остатков;

d) о невозможности сделать вывод относительно автокорреляции остатков.

7. Какое из условий означает наличие гетероскедастичности:

a) случайные возмущения независимы друг от друга;

b) случайные возмущения распределены по нормальному закону;

c) случайные возмущения обладают минимальной дисперсией;

d) случайные возмущения обладают постоянной дисперсией.

8. Мультипликативная модель:
a) представляет собой сумму компонент временного ряда;
b) представляет собой произведение компонент временного ряда;
c) представляет собой сумму и произведение соответствующих компонент;

d) представляет собой частное компонент временного ряда.

9. По данным о динамике цен на некоторый товар за 30 месяцев получены коэффициенты автокорреляции уровней временного ряда: , , , , , , 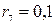. Охарактеризовать структуру временного ряда.

a) присутствует только тренд;

b) уровни ряда определяются только случайным фактором;

c) есть сезонные колебания порядка 6;

d) ничего нельзя сказать о структуре ряда.

10. Какой метод применяется для оценивания параметров идентифицированного уравнения?
a) МНК;
b) КМНК;
c) ДМНК;

d) ОМНК.

Вариант № 4.

Ситуационная (практическая) задача № 1

Проведено бюджетное обследование 22 случайно выбранных домохозяйств. Оно дало следующие результаты (в ден. ед.):

домохозяйство	Накопления, y	Доход, x1	Имущество, x2	домохозяйство	Накопления, y	Доход, x1	Имущество, x2
	9,4				18,3
	32,3				2,5
	5,7				27,2
	19,5
	27,4				15,7
	4,9
	17,3				11,9
					18,6
	5,2				28,2
	25,1				28,4
	30,6				17,3

Требуется:

1.Построить корреляционное поле между накоплениями и доходом. Выдвинуть гипотезу о тесноте и виде зависимости между показателями X1 и Y.

2. Оценить тесноту линейной связи между накоплениями и доходом с надежностью 0,99.

3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости накоплений от дохода.

4. Проверить статистическую значимость параметров уравнения регрессии с надежностью 0,99 и построить для них доверительные интервалы.

6. Для домохозяйства с доходом 50 ден. ед. дать точечный и интервальный прогноз накоплений с надежностью 0,99.

9. Найти коэффициенты парной и частной корреляции. Проанализировать их.

10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.

11.С помощью F-критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,99.

12. Для домохозяйства с доходом 50 ден. ед. и стоимостью имущества 20 ден. ед. дать точечный и интервальный прогноз накоплений с надежностью 0,99 .

Ситуационная (практическая) задача № 2

В таблице представлена динамика изменений курса акций промышленной компании в течение 14 месяцев.

T	январь	февраль	март	апрель	май	июнь	июль
y_t
T	август	сентябрь	октябрь	ноябрь	декабрь	январь	февраль
y_t

Требуется:

1. Проверить гипотезу о наличии тренда во временном ряде.

2. Рассчитать коэффициенты автокорреляции. Проверить наличие сезонных колебаний во временном ряде.

4. Дать точечный и интервальный прогноз курса акций компании на предстоящий апрель с надежностью 0,9.

Тестовые задания

Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению.

1. Значение переменной Y для некоторого наблюдения составило 12,

прогнозное значение Y в этом наблюдении составило 11,5. Чему равен остаток

в этом наблюдении:

a) 1;

b) 0,5;

c) 0,7;

d) 1,5.

2. Известно, что между величинами X и Y существует положительная связь. В каких пределах находится парный коэффициент корреляции?
а) от -1 до 0;
б) от 0 до 1;
в) от –1 до 1;

d) от 0 до ∞.

3. Пусть имеется модель регрессии , построенная по 20 наблюдениям. При построении доверительного интервала для коэффициента регрессии c доверительной вероятностью 0,99 нужно выбрать табличное значение:

а) ;

b) ;

c) ;

d) .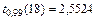

4. Мультиколлинеарность – это

a) линейная зависимость между объясняющей и объясняемой переменными;

b) линейная зависимость между объясняющими переменными;

c) линейная зависимость между объясняющей переменной и случайной составляющей уравнения;

d) тесная корреляционная зависимость между объясняющими переменными.

5. Тест на значимость отдельных параметров уравнения множественной регрессии называется

а) тестом Спирмена;

b) тестом Фишера;

c) тестом Голдфельда-Кванта;

d) тестом Стьюдента.

6. Какое из условий означает наличие автокорреляции:

a) случайные возмущения независимы друг от друга;

b) случайные возмущения распределены по нормальному закону;

c) случайные возмущения обладают минимальной дисперсией;

d) случайные возмущения обладают постоянной дисперсией.

7. Какое из следующих утверждений не верно в случае гетероскедастичности остатков?
а) Выводы по t и F- статистикам являются ненадежными;
б) Гетероскедастичность проявляется через низкое значение статистики Дарбина-Уотсона;
в) При гетероскедастичности оценки остаются эффективными;
г) Оценки являются смещенными.

8. Какая из составляющих временного ряда описывает долговременную, формирующую долгую (в длительной перспективе) тенденцию в изменении анализируемого признака Y.

a) случайная составляющая;

b) сезонная составляющая;

c) циклическая составляющая;

d) тренд.

9. По данным о динамике цен на некоторый товар за 24 месяца получены коэффициенты автокорреляции уровней временного ряда: , , , , , . Охарактеризовать структуру временного ряда.

a) присутствует только тренд;

b) уровни ряда определяются только случайным фактором;

c) есть сезонные колебания порядка 6;

d) ничего нельзя сказать о структуре ряда.

10. Модель считается идентифицированной, если:
a) среди уравнений модели есть хотя бы одно нормальное;
b) каждое уравнение системы идентифицируемо;
c) среди уравнений модели есть хотя бы одно неидентифицированное;
d) среди уравнений модели есть хотя бы одно сверхидентифицированное.

Вариант № 5.

Ситуационная (практическая) задача № 1

Предполагается, что объем предложения Y некоторого блага для функционирующей в условиях конкуренции фирмы линейно зависит от цены этого блага X1 и заработной платы X2 сотрудников фирмы, производящих данное благо. Статистические данные за 18 месяцев собраны в следующую таблицу:

месяц	Y, тыс. ед.	X1, руб.	X2 тыс. руб.	месяц	Y тыс. ед.	X1, руб.	X2, тыс. руб.

Требуется:

1.Построить корреляционное поле между объемом предложения блага и его ценой. Выдвинуть гипотезу о тесноте и виде зависимости между указанными показателями.

2. Оценить тесноту линейной связи между объемом предложения блага и его ценой с надежностью 0,9.

3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости объема предложения блага от его цены.

6. Дать точечный и интервальный прогноз с надежностью 0,9 объема предложения, если цена блага составит 30 руб.

Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,9 и построить для них доверительные интервалы.

9. Найти коэффициенты парной и частной корреляции. Проанализировать их.

10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.

11.С помощью F -критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,9.

12. Дать точечный и интервальный прогноз с надежностью 0,9 объема предложения блага для фирмы, если цена блага составит 30 руб., а заработная плата сотрудников фирмы равна 11 тыс. руб.

Ситуационная (практическая) задача № 2

Имеются поквартальные данные по товарообороту некоторой компании в 1999-2008 гг.

Год	Товарооборот, млн. руб.	Год	Товарооборот, млн. руб.
	100,0		95,7
	93,9		98,2
	96,5		104,0
	101,8		99,0
	107,8		98,8

Требуется:

1. Проверить гипотезу о наличии тренда во временном ряде.

2. Рассчитать коэффициенты автокорреляции. Проверить наличие сезонных колебаний во временном ряде.

4. Дать точечный и интервальный прогноз товарооборота компании компании на 2011 год с надежностью 0,99.

Тестовые задания

Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению.

1. С помощью какого метода можно найти оценки параметра уравнения линейной регрессии:
a) метода наименьших квадратов;
b) корреляционно-регрессионного анализа;
c) дисперсионного анализа;

d) метода серий.

2. Уравнение регрессии, описывающее зависимость удельных постоянных расходов от объема выпускаемой продукции имеет вид: . Чему может быть равен линейный коэффициент парной корреляции?

a) -0,9;

b) 0,75;

c) 1,5;

d) -0,75.

3. Линейный коэффициент парной корреляции для величин 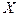и равен 0,8. Чему равен коэффициент детерминации для линейного уравнения парной регрессии, построенного по этой выборке?

a) 0,64;

b) 0,894;

c) 0,2;

d) 0,4.

4. По 30 наблюдениям построено уравнение регрессии . Каким квантилем нужно воспользоваться при проверке статистической значимости коэффициентов частной корреляции для этого уравнения?

a) ;

b) ;

c) ;

d) .

5. По формуле вычисляется

a) статистика χ²для проверки наличия мультиколлинеарности в модели регрессии;

b) вектор оценок коэффициентов для уравнения множественной регрессии;

c) критерий для проверки адекватности модели;

d) прогнозное значение исследуемого показателя.

6. С помощью какого критерия проверяют наличие автокорреляции остатков?

a) Дарбина-Уотсона;

b) Фишера;

c) Голдфельда-Кванта;

d) Стьюдента.

7. Следствием гетероскедастичности является

a) несостоятельность оценок параметров уравнения, полученных по МНК;

b) смещенность оценок параметров уравнения, полученных по МНК;

c) неприменимость статистических тестов;

d) ненадежность оценок параметров уравнения, полученных по МНК.

8. Какая из составляющих временного ряда описывает конъюнктурные факторы, формирующие изменения анализируемого признака, обусловленные воздействием долговременных циклов экономической, демографической или солнечной активности

a) тренд;

b) сезонная составляющая;

c) циклическая составляющая;

d) случайная составляющая.

9. Какая из представленных моделей временного ряда является моделью тренда?

a) y_t*= at+b+ε;

b) y_t*= a₀+a₁t+a₂cos(kt)+a₃sin(kt)+ε;

с) y_t*= ay_t-1+b+ε;

d) y_t*= a₀+a₁t+a₂t²+b₁δ₁+ b₂δ₂+ ε.

10. Для каких видов систем параметры отдельных эконометрических уравнений могут быть найдены с помощью обычного МНК?
a) система нормальных уравнений;
b) система независимых уравнений;
c) система рекурсивных уравнений;
d) система взаимозависимых уравнений.

Вариант № 6.

Ситуационная (практическая) задача № 1

По 16 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x₁(% от стоимости фондов на конец года) и от ввода в действие новых основных фондов x2(%).

Номер предприятия	y	X1	X2	Номер предприятия	y	X1	X2
			4,7				7,5

			5,8				8,4
			5,8				8,7
			6,1				8,9
			6,5				9,1
			6,8
			6,9				10,5

Требуется:

2. Оценить тесноту линейной связи между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации с надежностью 0,95.

6. Дать точечный и интервальный прогноз с надежностью 0,95 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 33% рабочих.

9.Найти коэффициенты парной и частной корреляции. Проанализировать их.

11.С помощью F -критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,95.

12. Дать точечный и интервальный прогноз с надежностью 0,95 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 33% рабочих, а ввод в действие новых основных фондов составляет 7%.

Ситуационная (практическая) задача № 2

Имеются помесячные данные по объему платных услуг населению в 2010 г.

месяц	Объем платных услуг, млн. руб.	месяц	Объем платных услуг, млн. руб.	месяц	Объем платных услуг, млн. руб.
январь	28,91	апрель	39,14	июль	38,36
февраль	31,96	май	34,93	август	41,4
март	32,48	июнь	35,26	сентябрь	44,39

Требуется:

1.Проверить гипотезу о наличии тренда во временном ряде.

2. Рассчитать коэффициенты автокорреляции. Проверить наличие сезонных колебаний во временном ряде.

3.Оценить параметры линейной трендовой модели, проверить статистическую значимость соответствующего уравнения регрессии с надежностью 0,95.

4.Дать точечный и интервальный прогноз объема платных услуг на декабрь 2010 г. с надежностью 0,95.

Тестовые задания

Необходимо из предложенных вариантов ответа на вопрос теста выбрать единственно верный, по Вашему мнению.

1. Какой метод используется для количественной оценки силы воздействия одних факторов на другие:
a) корреляционный анализ;
b) регрессионный анализ;
c) метод средних величин;
d) дисперсионный анализ.

2. По 25 наблюдениям построено уравнение регрессии . Коэффициент детерминации оказался равным 0,6. - статистика равна:

a) 12,938;

b) 17,25;

c) 23,333;

d) 34,5.

3. По 25 наблюдениям получено уравнение регрессии . Зависимость от выражается уравнением:

а) ;

b) ;

c) ;

d) .

4. При оценке заработной платы для работников некоторой отрасли в качестве одного из факторов рассматривается образование работника: «есть высшее образование», «есть среднеспециальное образование», «есть общее среднее образование». Сколько фиктивных переменных необходимо использовать для моделирования данного признака?

a) 3;

b) 2;

c) 1;

d) нисколько.

5. Уравнение регрессии построено по 29 наблюдениям. Каким квантилем нужно воспользоваться для проверки адекватности этого уравнения на уровне значимости 0,01?

a) ;

b) ;

c) ;

d) .

6. Причиной автокорреляции остатков может являться

a) неверная спецификация модели;

b) корреляция между случайной составляющей и независимой переменной;

c) корреляция между случайными составляющими в разных наблюдениях;

d) корреляция между независимыми переменными.

7. Пусть рассматривается модель регрессии , построенное по наблюдениям. Какое из нижеперечисленных условий не входит в условия Гаусса-Маркова:

a) ;

b) ;

c) cov( ) = 0, i≠j;

d) .

8. Если наибольшее по модулю значение имеет коэффициент автокорреляции первого порядка, исследуемый ряд содержит…

a) только случайную компоненту;

b) сезонные колебания с периодичностью в один момент времени;

c) линейный тренд;

d) нелинейный тренд.

9. Уравнение тренда , описывающее динамику цены (руб.) на некоторый товар, построено по месячным данным за 2005-2006 годы. Каков прогноз цены на этот товар на апрель 2007 года?

a) 15,52 руб.;

b) 77,56 руб.;

c) 24,64 руб.;

d) 14, 38 руб.

10. Эндогенные переменные – это…
a) зависимые переменные;
b) независимые переменные;
c) датированные предыдущими моментами времени;

d) все входящие в модель переменные.

Вариант № 7.

Ситуационная (практическая) задача № 1

Изучается влияние стоимости основных и оборотных средств на величину валового дохода торговых предприятий. Для этого по 20 торговым предприятиям были получены данные, приведенные в таблице.

№ пред-приятия	Валовой доход за год, y, млн.руб.	Среднегодовая стоимость, млн. руб.	№ пред-приятия	Валовой доход за год, y, млн.руб. основных фондов	Среднегодовая стоимость, млн. руб.
основных фондов	оборотных средств	основных фондов	оборотных средств

Требуется:

1.Построить корреляционное поле между валовым доходом и стоимостью основных фондов. Выдвинуть гипотезу о тесноте и виде зависимости между этими показателями.

2. Оценить тесноту линейной связи между валовым доходом и стоимостью основных фондов с надежностью 0,95.

3. Рассчитать коэффициенты линейного уравнения регрессии для зависимости валового дохода от стоимости основных фондов.

6. Дать точечный и интервальный прогноз с надежностью 0,95 величины валового дохода для предприятия с основными фондами 50 млн. руб.

9. Найти коэффициенты парной и частной корреляции. Проанализировать их.

10. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.

11.С помощью F -критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,95.

12. Дать точечный и интервальный прогноз с надежностью 0,95 величины валового дохода для предприятия, на котором стоимость основных фондов составляет 50 млн. руб., а стоимость оборотных средств - 75 млн. руб.

Ситуационная (практическая) задача № 2

Динамика выпуска продукции за 1994-2011 гг. представлена в таблице.

Год	Выпуск , ед	Год	Выпуск, ед	Год	Выпуск, ед
				12 Следующая ⇒ ©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.