Здавалка
Главная | Обратная связь

C r y p t o g r a p h i c a l g o r i t h m 8 страница

⇐ ПредыдущаяСтр 8 из 15Следующая ⇒
ш.с.2 Ю П Я Т Б Н Щ М С Д Т Л Ж Г П С Г Х С Ц Ц
С2


Возможны 15 вариантов (номер варианта обозначим буквой k) расположения слова КОРАБЛИ в каждом из двух исходных сообщений (и. с. 1, и. с. 2).

Вначале для каждого из 15 вариантов расположения слова КОРАБЛИ в и. с. 1 найдем соответствующий участок и. с. 2. Имеем:

C2-C1

 

 

T1
T2 T21 T22 T23 T24 T25 T26 T27


Поэтому для участка и. с. 2 получаем следующие 15 вариантов:

k
T21
T22
T23
T24
T25
T26
T27


Теперь для каждого из 15 вариантов расположения слова КОРАБЛИ в и. с. 2 найдем соответствующий участок и. с. 1. Имеем:

C1-C2

 

 

T2
T1 T11 T12 T13 T14 T15 T16 T17


Поэтому для участка и. с. 1 получаем следующие 15 вариантов:

k
T11
T12
T13
T14
T15
T16
T17

 

Заменим порядковые номера в найденных вариантах участков и. с. 1 и и. с. 2 на буквы русского алфавита. Получаем следующие таблицы:

k
  К К Ц Е Л Ж А Э Ь Г Х О Л Л В
  О Ь К П Л Д Б Я З Щ Т П П Ж Е
участок Э М С Н Ж Г Б К Ы Ф С С И З Ч
и.с.2 Ы Б Э Ц У С Щ М Д Б Б Ш Ч З Е
  В Ю Ч Ф Т Ь Н Е В В Щ Ш И Ж Р
  Э Б Ю Ы Д Ц П М М Г В Т Р Щ О
  Я Ы Щ В Ф Н К К Б А Р О Ч М М

 


k
  К К Э О И Н У Ц Ш Р Ю Е И И С
  О Б Т Н С Ч Ь Э Ф В К Н Н Х Ц
участок Г Ф П У Щ Э Я Ц Д М П П Ч Ш И
и.с.1 Д Я Г К Н П Ж Ф Ы Я Я З И Ш Ь
  А Д Л О Р З Х Э А А И К Щ Ы Т
  О Ф Ч Щ С Я Ж К К Т У Г Е Ы З
  Т Х Ч П Э Д З З Р С Б Г Щ Е Е


Из таблиц видно, что осмысленными являются варианты:

и.с.1 = К О Г Д А О Т . . . . . . . К О Р А Б Л И
и.с.2 = К О Р А Б Л И . . . . . . . В Е Ч Е Р О М

Задача 4.Для зашифрования текстов каждую букву заменяли парой цифр. При этом разные буквы текста заменялись разными парами, а одинаковые - одинаковыми. Даны два зашифрованных текста:

79 92 38 98 95 91 34 95 73 77 96 92 78 95 73 98 92 96 92 72 98 96 77 72 92 34 77 96 75 90 76 95 38 98 92 70 33 90 96 79 90 96 77 98 95 90 38 77 70 70 90 98 74 92 96 98 96 77 72 92 34 77 96 75 73 77 96 92 98 74 92 79 96 90 79 92 96 98 94 90 76 98 74 92 95 96 96 92 73 79 92 33 98 95 32 92 90 93 38 92 96 73 94 90 91 96 91 73 92 98 74 95 73 33 72 96 90 34 95 73 73 91 36 71 92 33 98 98 90 77 38 92 38 72 91 73 92 96 70 95 33 92 38 33 92
71 75 74 39 74 73 74 72 30 73 74 78 33 79 98 94 78 36 79 97 72 29 78 74 96 74 92 30 38 79 70 72 94 78 79 22 92 92 79 98 37 70 92 74 94 77 74 93 31 78 74 70 39 79 71 75 94 98 70 39 97 92 72 22 23 39 78 94 70 74 76 78 94 78 78 30 77 39 94 74 75 94 39 79 38 94 70 73 79 77 79 78 39 94 75 94 70 73 75 74 76 94 39 74 96 74 76 78 74 96 79 94 39 79 71 30 27 39 79 32 71 75 74 39 74 73 74 72 74 92 71 75 94 98 35 22 92 72 22 23 39

Известно, что один из них соответствует сообщению на русском языке, а другой - на английском (в текстах строчные и заглавные буквы не различались, а пробелы и знаки препинания опускались). Определите, какой шифрованный текст соответствует сообщению на русском языке.

Решение

Для решения этой задачи достаточно было заметить, что при указанном способе зашифрования количество различных букв в исходном тексте совпадает с числом различных пар в криптограмме. Первая из приведенных в условии задачи криптограмм содержит 23 различные пары, а вторая — 29. Так как латинский алфавит состоит из 26 букв, английскому исходному тексту может соответствовать только первая криптограмма.

Задача 5.Докажите, что десятичная запись квадрата натурального числа не может состоять из одинаковых цифр.

Решение

Квадрат натурального числа может оканчиваться только на цифры 0, 1, 4, 5, 6, 9. Число 0ј0 натуральным не является. Число 5...5 не может быть квадратом, так как оно делится на 5, но не делится на 25. Аналогично 6...6 ≠ n2, так как это число делится на 2, но не делится на 4. Числа 4ј4 и 9ј9 являются полными квадратами в том и только том случае, когда полным квадратом будет 1ј1.

Докажем, что 1...1 ≠ n2. Предположим, что это не так: существует такое натуральное число n, что 1...1 = n2. Тогда n = 10k ± 1 и, следовательно, 100k2 ± 20k = 1...10 ⇔ 10k2 ± 2k = 1...1. Получили противоречие: нечетное число равно четному.

Гг

Задача 1.Заполните неокрашенные клетки таблицы числами от 1 до 9. При этом, сумма цифр в каждой горизонтальной неокрашенной цепочке должна совпадать с числом, указанным слева от цепочки, а в каждой вертикальной неокрашенной цепочке - с числом, указанным сверху от цепочки. В каждой цепочке ни одна цифра не должна повторяться.

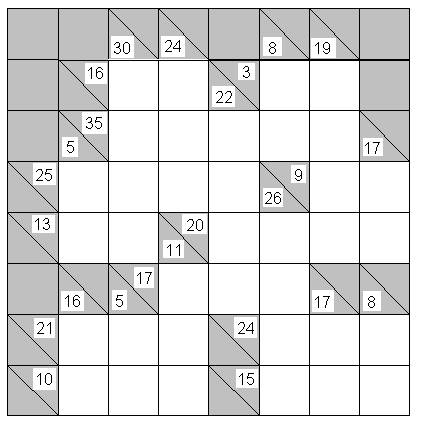
Решение

Единственно возможное заполнение таблицы:

Задача 2. Бильярдные шары плотно уложены в правильный треугольник с основанием из 2006 шаров. На каждом шаре написано число. Сумма трех чисел, написанных на шарах при вершинах исходного треугольника, а также любых треугольников со сторонами, параллельными исходному треугольнику, равна 0. Какие числа могут быть написаны на шарах?
Решение

Рассмотрим фрагмент исходного треугольника, который представляет собой правильный треугольник, со стороной из четырех шаров. Пусть на верхнем шаре написано число а, а на одном из примыкающих снизу шаров – число b. Из условия задачи следует, что сумма чисел на любых трех попарно примыкающих шарах равна нулю. Поэтому числа на остальных шарах выражаются через а и bкак показано на рисунке. Видим, что в вершинах фрагмента стоит число а, следовательно а = 0. Совершенно аналогично (рассмотрев правильный треугольник, со стороной из пяти шаров) доказывается, что b = 0.

Задача 3.Пусть a1, a2, a3, … и b1, b2, b3, … числовые последовательности периодов 16 и 2006 соответственно. Найдите период последовательности a1, b1, a2, b2, a3, b3, …. (Периодом последовательности x1, x2, x3, … называется наименьшее натуральное число T, такое, что для всех натуральных n верно равенство xn+T = xn ).

Решение

Разобьём последовательность {xn} на пары (х1,х2), (х3,х4).… При записи в терминах исходных последовательностей, полученная последовательность пар имеет вид

(a1,b1), (a2,b2), ….

Период этой последовательности пар равен c=НОК(16,2006)=16048, так как равенство пар означает равенство их первых и равенство их вторых элементов. Поэтому, при всех натуральных n верно равенство

xn=xn+2с

Покажем, что 2с – наименьшее число с таким условием.

Пусть период последовательности {xn} равен t. Тогда число 2c должно делиться на число t. (Повторение значений в последовательности со смещением на 2сшагов должно быть получено как несколько смещений с шагом t).

Если t четно, t=2k, то из верных при всех натуральных m равенств

x2m-1+t=x2m-1
x2m+t=x2m

Следуют равенства

am+k=am
bm+k=bm

Таким образом, k делится на наименьшее общее кратное периодов исходных последовательностей. Отсюда t=2НОК(16, 2006)=32096.

При нечетном t первая последовательность является «сдвигом» второй, что противоречит различию длин их периодов.

Задача 4.Для зашифрования сообщения на английском языке составляются две таблицы размера 5×5. В клетки каждой таблицы в неизвестном порядке вписаны буквы укороченного английского алфавита (v и w отождествлены), так что каждая буква алфавита встречается в каждой таблице один раз. Букву, расположенную в i-ой строке и j-м столбце первой таблицы обозначим через аij, а букву второй таблицы - через bij. При зашифровании сообщение разбивается на пары подряд идущих букв. Пара вида аijblm заменяется при i ≠ l парой bimalj, а при i = l - парой bljaim. В результате зашифрования сообщения

c r y p t o g r a p h i c a l g o r i t h m

был получен один из следующих шифртекстов:

p a b d g l i u r c a v t h o t u e a d s p,
d s z q u p h s b q i j d b m h p s j u i n.

Определите, какой именно? Ответ обоснуйте.

Решение

Указанный в задаче способ зашифрования текста обладает следующим свойством. Если пара ab заменяется на пару cd, то пара dc перейдет в пару ba. Проверяем наличие этого свойства в предложенных открытом и зашифрованных текстах. Для первого шифртекста первая же пара сr переходит в pa, а apпереходит в rc. Есть и другая пара - to переходит в gl, а lg переходит в ot:

c r y p t o g r a p h i c a l g o r i t h m

⇐ Предыдущая3456789101112Следующая ⇒






©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.