Главная | Обратная связь

ЕПОЕЬРИТСГХЖЗТЯПСТАПДСБИСТЧК

Прочтите исходное сообщение.

Решение

Отсутствует.

Задача 12. Для зашифрования фразы был взят кубик Рубика с нанесенными на гранях русскими буквами. Развертка кубика показана на рис. 1.

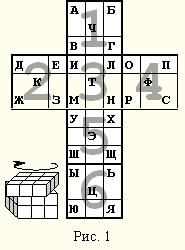
Затем грани последовательно повернули по часовой стрелке на 90° определенное число раз: грань 1 – шесть раз; грань 2 – три раза; грань 3 – один раз; грань 4 – четыре; грань 5 – два и, наконец, грань 6 – пять раз. Затем каждая буква фразы отыскивалась на грани кубика и заменялась буквой этой же грани, следующей за ней по часовой стрелке (например, на рис. 1 буква A переходит в букву Б, буква П в С). Буквы, находящиеся в центре грани, не заменяются. В результате получилась строка:

Решение

Заметим, четырёхкратный поворот грани ничего не изменяет, а трёхкратный поворот по часовой стрелке эквивалентен одному повороту против часовой стрелки. Таким образом, чтобы узнать, как были расположены буквы при шифровании, необходимо повернуть грань 1 – два раза; грань 2 – один раз (против часовой стрелки); грань 3 – один раз; грань 4 – не поворачивать; грань 5 – два и, наконец, грань 6 – один раз. После этого, исходя из расположения букв на полученном кубике, можно найти исходное сообщение, заменяя буквы шифртекста на буквы, стоящие в клетках против часовой стрелки. Отметим, что нет необходимости узнавать, куда перешли все написанные на кубе буквы. Достаточно узнать расположение букв шифртекста после описанных преобразований. После этого следует выделить клетку, следующую против часовой стрелки за клеткой с рассматриваемой буквой шифртекста. Затем необходимо осуществить обратное преобразование, и в выделенной клетке на исходном кубе окажется соответствующая буква открытого текста.

Задача 13.Известно, что число N = 202718099 является произведением двух простых чисел p и q , а количество натуральных чисел, меньших N и взаимно простых с N, равно 202687920. Найдите числа p и q.

Ответ

10091 и 20089

Задача 14.Подсчитайте, сколько всего существует натуральных чисел, которые не превосходят число 841 и не имеют с ним общих делителей, отличных от 1.

Решение

Заметим, что 849 = 29² и 29 – простое число. Теперь нетрудно сообразить, что существует 29(29 - 1) = 812 натуральных чисел, которые не превосходят число 841 и не имеют с ним общих делителей, отличных от 1.

Гг

Задача 1.В нейрокомпьютере используется упрощённая модель нейрона – клетки головного мозга (см. рис. 7). По четырём каналам x₁, x₂, x₃, x₄ в клетку поступают нули и единицы, из которых внутри неё формируется сумма S = a₁ x₁ + a₂ x₂ + a₃ x₃ + a₄ x₄ ( a₁, a₂, a₃, a₄ – целые). Затем S сравнивается с некоторым целым параметром c, и если S ≥ c , то на выходе клетки формируется значение y = 1, иначе – y = 0.

Найдите какие-либо целые параметры a₁, a₂, a₃, a₄, c такого нейрона, чтобы y = 1 на наборах (1,0,1,0), (1,1,1,0), (0,0,1,0), (1,0,0,1), (1,0,1,1), (0,0,1,1), (1,1,1,1) и y = 0 – на остальных наборах.

Решение

Задача 2.

Для прохода в учреждение необходимо предъявить пятизначную комбинацию, состоящую из нулей и единиц. Устройство распознавания представляет собой упрощённую модель нейрона – клетки головного мозга (см. рис. 6).

Пятизначная комбинация x₁, x₂, x₃, x₄, x₅ по пяти каналам поступает в клетку, где её компоненты умножаются на фиксированные целые числа a₁, a₂, a₃, a₄, a₅ , и вычисляется сумма S = a₁ x₁ + a₂ x₂ + a₃ x₃ + a₄ x₄ + a₅ x₅ . Проход в учреждение открывается, только если S ≥ c где c – некоторое фиксированное целое число. В табл. 1 представлены те комбинации, при предъявлении которых проход открывается, а в табл. 2 – для которых проход закрыт. Найдите ещё одну комбинацию, открывающую проход в учреждение.

		Таблица 1						Таблица 2
	1,0,1,1,0	1,1,0,1,0	1,1,1,1,1		1,0,1,0,0	0,0,1,1,0	1,1,0,1,1	1,0,1,1,1

Решение

Для комбинации 1,0,1,1,0 – проход открыт, а для 0,0,1,1,0 – проход закрыт. То есть при изменении значения первой координаты с 1 на 0 значение суммы становится меньше c , поэтому очевидно, что . Аналогично:

Поэтому заведомо пройдет комбинация, максимизирующая значение суммы S, а именно 1,1,1,1,0. Отметим, что задача составлена таким образом, что других решений нет.

Задача 3.Для зашифрования натурального числа m используется граф, представляющий собой множество вершин, некоторые из которых соединены друг с другом прямой линией. Вершины графа, соединенные друг с другом, называют соседними. Зашифрование состоит в выполнении следующих действий. В вершины графа записываются натуральные числа так, чтобы их сумма была равна m. Затем к числу в каждой вершине прибавляются числа в соседних вершинах. В результате получается граф, в котором «зашифровано» число m. Пример: для зашифрования числа 8 будем использовать граф на рис. 1. В его вершины поместим числа, сумма которых равна 8 (рис. 2). Затем к каждому числу прибавим числа в соседних вершинах. Результат зашифрования указан на рис. 3. На рис. 4 приведен результат зашифрования некоторого числа. Найдите его.

Решение Граф, используемый в задаче, обладает следующим свойством: из множества всех его вершин можно выделить такое подмножество V (отмеченное на рис. 5 кружочками), что любая вершина графа лежит в окрестности ровно одной вершины из V. Окрестностью вершины графа называют множество соседних с ней вершин, включая её саму. Очевидно, что искомое число равно сумме чисел, расположенных в вершинах из множества V: .

Задача 4.Крокодил Гена и Чебурашка могут связываться по двум каналам: радиоканалу и оптическому каналу. Используя эти каналы, они хотят договориться о кодовой комбинации сейфа, составленной из 20 букв К, З, С или Ч. Для этого Гена по оптическому каналу передаёт случайную комбинацию из 20 вспышек, причём каждая вспышка может быть красного (К), синего (С) или зелёного (З) цвета. Для каждой вспышки Чебурашка наугад выбирает светофильтр. Если его цвет совпадает с переданным цветом, то срабатывает датчик, а если не совпадает, то цвет вспышки остаётся для Чебурашки неизвестным. После замера всех вспышек Чебурашка по радиоканалу сообщает, какие светофильтры он выбрал. В результате Гена узнаёт номера вспышек, цвет которых Чебурашка определил. Гена устанавливает комбинацию на сейфе так: если цвет очередной вспышки Чебурашке определить удалось, то выбирается буква, соответствующая цвету вспышки (К, З либо С), если нет – выбирается Ч.

Шапокляк прослушивает радиоканал и «встроилась» в оптический канал. На пути передаваемых вспышек она выставляла свои светофильтры: ККЗЗЗСКСКСЗЗСКСКСКЗКи одновременно передавала вспышки соответствующих цветов Чебурашке. Срабатывание датчика у неё произошло на 6, 10, 11, 14, 17 и 19 вспышках. Чебурашка, не зная о вмешательстве, сообщил по радиоканалу свои цвета: СКЗККККЗЗККССККЗСЗСК. С учётом собранной Шапокляк информации, определите число кодовых комбинаций, которые гарантированно не откроют сейф.

Решение

Сравним посимвольно последовательности цветов, приведённые в условии и сформируем таблицу:

С К З К К К К З З К К С С К К З С З С К Светофильтры Чебурашки К К З З З С К С К С З З С К С К С К З К Светофильтры Шапокляк           *       * *     *

Задача 5.Известно, что число 14197777 равно остатку от деления на 56887111 некоторого числа x, возведённого в куб. Числа x и 56887111 имеют общий делитель, отличный от 1, а число56887111 является произведением двух простых чисел. Найдите хотя бы одно такое числоx.

Решение

Пусть y=14197777, N=p·q =56887111, p,q – простые числа. По условиюНОД(x,N)=p>1 , то есть x=t·p, где t – натуральное число.

Так как y=r_N(x³) - остаток от деления на N числа x³, то НОД(y,N)=p.Вычисляя НОД(14197777, 56887111), находим, что p=10667, тогда y=1331·p, аq=N/p=5333. Делим обе части уравнения

1331·p= r_N((t·p)³)

на p, получаем:

1331= r_N( t³· p²) = r₅₃₃₃( t³· 10667²) = r₅₃₃₃( t³).

Поэтому t = ³√1331 = 11 и x = t·p = 11·10667 = 117337.

Задача 6.В концах диаметра окружности расположены числа 1 и 5, разбивающие окружность на две дуги. Совершим по окружности n оборотов по часовой стрелке, приняв за начало обхода один из концов диаметра. После прохождения каждой имеющейся на данный момент дуги делим её пополам и в середине записываем число (3x +3y)/2 , где х и у – числа, стоящие на концах пройденной дуги, взятые в порядке направления обхода. Найдите сумму всех записанных чисел после n оборотов.

Решение

Сначала заметим, что после первого оборота количество дуг равно 2², после второго – 2³ , после последнего – 2ⁿ⁺¹.Пусть после оборота с номеромk, 1≤k≤n в точках деления окружности на дуги расположены числа x₁, x₂,...,x₂^k+1. Тогда в ходе оборота с номером k+1 на окружности появятся следующие новые числа

y₁ = (3x₁ + 3x₂)/2, y₂ = (3x₂ + 3x₃)/2 , ... , y₂^k+1 = (3x₂^k+1 + 3x₁)/2.

Очеидно, что

y₁ + y₂ + .... + y₂^k+1 = 3( x₁ + x₂ + .... + x₂^k+1).

Значит, после k+1 оборота сумма всех чисел на окружности возрастёт в 4 раза. Если учесть, что первоначальная сумма чисел на окружности равнялась 6, то получаем окончательный ответ.

Задача 7.В текстовом сообщении на русском языке, записанном без знаков препинания и пробелов, переставили буквы: