 |
|
Наблюдающие устройства
Изучив модальное управление, мы убедились, что динамическими свойства систем можно управлять. В доказательство можно привести такой пример.
Применим к системе
x’ = A*x + B*u (1)
процедуру перехода к расширенному вектору состояния
v’ = F*v,
где F = {fij} – матрица коэффициентов динамики системы.
Можно убедиться, что при вводе обратной связи с коэффициентом lij по переменной из расширенного вектора состояния, например vj, правая часть i-го скалярного уравнения из системы, описывающей динамику управляемого комплекса, будет изменяться:
 , где
, где 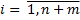 .
.
От правой части зависит скорость изменения этой переменной состояния vi’,а значит, и динамика системы – траектория ее движения во времени.
Однако, величину vj надо знать.
Изучая модальный регулятор, мы предполагали, что все переменные x, u, а значит и v – известны. Но так бывает не всегда.
Часто при решении задач модального управления в САУ бывают доступны для измерения не все переменные состояния (ПС), а только некоторые выходы.
Рассмотрим, как можно косвенно определить компоненты вектора переменных состояния управляемого объекта, недоступные прямому измерению.
Состояние x(t) называется наблюдаемым, если для момента наблюдения t0 можно однозначно определить состояние x(t0) по данным измерений y(t) и u(t) на конечном интервале t0 <= t <= tk. Это возможно, если матрица наблюдения Qн = [CT ATCT (AT)2CT … (AT)n-1CT] имеет ранг, равный рангу динамической системы n.
Пусть объект управления (ОУ) описывается уравнениями
x’ = A*x + B*u, (2)
y = Cx.
Для измерения выходного сигнала имеются датчики, моделируемые «матрицей выхода» С.
Нам следует оценить вектор ПС x^ по измеренным значениям u и y.
Включим параллельно объекту управления модель, имеющую такую же структуру:
С выхода матрицы N на сумматор поступает сигнал коррекции состояния. Сигнал ошибки – разность между выходными координатами объекта и модели
e = y – y^ формирует этот сигнал коррекции состояния.
Когда процесс итеративной коррекции состояния модели сойдется, ПС модели будут повторять ПС объекта. Это «наблюдатель Льюинбергера».
Таким образом, работа наблюдающего устройства (НУ) для оценки ПС объекта управления x^ строится (организуется) согласно зависимостям:
x’^ = Ax^ + Bu + N(y-y^)
y^ = Cx^, (3)
где x^ и y^ - соответственно оценочные векторы ПС и выхода НУ;
N = {nij} - матрица коэффициентов передачи наблюдателя (или его настройки0, подлежащих определению.
Уравнения (3) описывают динамическую систему, входами которой являются u, процесс y, а выходами – вектор x^, который необходим для построения нового управляющего воздействия на объект управления через модальный регулятор.
Заметим, если модальный регулятор – это матрица коэффициентов обратных связей L, то НУ – это динамическая система, порядок которой совпадает с порядком объекта управления.
Объединим уравнения системы (3):
x’^ = Ax^ - NCx^ + Bu + Ny, (4)
и заменим выходной сигнал объекта управления согласно выражению
y = Cx, тогда
x’^ = Ax^ - NCx^ + Bu + NCx. (5)
Выделим разность ε = x^ - x. Назовем ее ошибкой оценки вектора ПС и заметим, что она не равна переменной коррекции e. Введем ее в выражение (5) и вычтем из последнего уравнение объекта управления (2):
x’^ = Ax^ - NCε + Bu
-
x’ = Ax + Bu
ε’ = A ε - NC ε = (A-NC) ε = H ε (6)
Таким образом, описание НУ сведено к однородному дифференциальному уравнению
ε’ = H ε, (6’)
где H = {hij} – матрица динамических свойств наблюдателя.
Если в уравнении (6) или (6’) выбрать элементы матрицы H такими, чтобы система была устойчивой (например, любые стандартные формы описывают устойчивые системы), получим
lim ε(t) = 0 | t ->inf.
То есть, с течением времени ПС наблюдателя стремятся к ПС объекта управления.
Элементам матрицы H можно поставить в соответствие любое желаемое распределение корней характеристического уравнения
D(s) = det[sE – H] = 0, (7)
пользуясь, например, одной из стандартных форм, изученных при знакомстве с модальным управлением.
Для этого так же, как и при расчете коэффициентов модальных регуляторов приравнивают коэффициенты при одинаковых степенях оператора “s” стандартной формы и уравнения (7). Это позволяет найти выражения для определения элементов матрицы наблюдателя N через параметр ω0 стандартных форм.
Уравнение наблюдающего устройства в конечном итоге приобретает вид
x’^ = Ax^ + Bu + Ne. (8)
В целях построения модели запишем его иначе:
x’^ = Ax^ + Bu + Ny – NCx^ =
= (A – NC)x^ + Bu + Ny =
= Hx^ + Bu + Ny,
где H – определяет динамику наблюдающего устройства,
u и y – внешние воздействия на модель, которая и реализует НУ.