 |
|
III.2.2. Феноменологическое описание поведения диэлектриков в электрическом поле в теории электрических цепей
В теории электрически цепей поляризация диэлектрика, помещенного в электрическое поле между двумя проводниками–электродами, к которым в квазистационарных условиях прикладывается постоянное, а в динамических условиях – переменное напряжение V, моделируется емкостным элементом (двухполюсником или конденсатором), который характеризуется емкостным током Ic, емкостным сопротивлением Xc, зарядом Qc и емкостью Сх. В идеальном случае линейного емкостного элемента (в отсутствие токов утечки, поляризации электродов, инжекции зарядов из них и т.п.) при постоянном напряжении V:
 ;
;  (1.43)
(1.43)
При изменении напряжения по синусоидальному закону с круговой частотой w для идеального конденсатора:
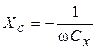 ;
;  (1.44)
(1.44)
При этом ток Ic опережает по фазе напряжение Vc на угол 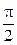 .
.
При наличии тока утечки, обусловленного, в первую очередь, проводимостью диэлектрика, емкостной двухполюсник характеризуется, кроме емкостных параметров, также активной проводимостью Gx, обратным сопротивлением Rx и активным током IR, совпадающим по фазе с прикладываемым напряжением V:
 (1.45)
(1.45)
Такой двухполюсник характеризуется также индуктивностью Lx (отрицательной емкостью), однако при частотах, значительно меньших, чем резонансная (w<<wр=  ), индуктивностью обычно пренебрегают.
), индуктивностью обычно пренебрегают.
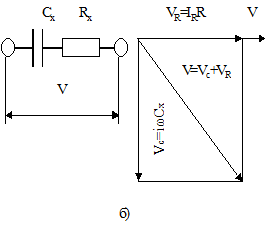
Таким образом, сочетание (параллельное или последовательное) идеального линейного конденсатора и сопротивления, т.е. двухполюсника Сх – Rx моделирует процессы поляризации и проводимости в диэлектрике, находящемся между электродами при приложении напряжения V (Рис. 1.8).

| 
|
| Рис. 1.8. Схемы двухполюсников Сх-Rx с параллельным (а) и последовательным (б) соединением элементов и соответствующие диаграммы токов и напряжений в них |
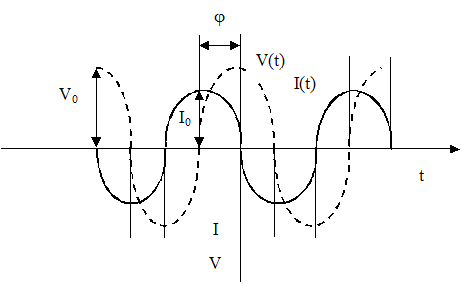
В моделях с параллельным соединением элементов суммарный ток опережает (см. рис. 1.8 а), а с последовательным соединением элементов суммарное напряжение отстает (см. рис. 1.8 б) от приложенного постоянного напряжения на угол j [ ]. При синусоидальном установившемся приложении напряжения суммарное напряжение и ток, функции времени, представляют собой синусоиды со сдвигом фаз на угол j (Рис. 1.9).
|
Рис. 1.9. Синусоиды 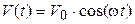 и и  для параллельного двухполюсника Сх - Rx для параллельного двухполюсника Сх - Rx
|
В терминах комплексных чисел:
 ;
;  (1.46)
(1.46)
где: V и I – комплексные амплитуды напряжения и тока соответственно:
V=V0;  (1.47)
(1.47)
Для обобщенного описания параметров двухполюсников Сх-Rx (емкости или емкостного сопротивления Хс и активного сопротивления Rx или проводимости Gx) в терминах комплексных чисел в теории цепей используют комплексные величины – импеданс (комплексное сопротивление) Z*(w) и обратную ему величину – адмитанс (комплексную проводимость) Y*(w) [ ]: Для параллельного двухполюсника Сx – Rx:
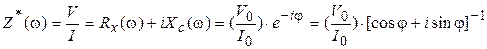 (1.48)
(1.48)
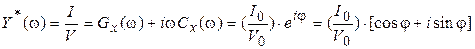 (1.49)
(1.49)
Из этих соотношений следует:
 ;
;  (1.50)
(1.50)
Угол d дополнительный к углу j (  ), соответствует углу потерь, тангенс которого для параллельного двухполюсника Сх – Rx равен:
), соответствует углу потерь, тангенс которого для параллельного двухполюсника Сх – Rx равен:
 , (1.51)
, (1.51)
а для последовательного:
 (1.52)
(1.52)
По величине tgdх равен ctg j и определяет потери энергии W при прохождении тока в двухполюснике Сх –Rx. Для параллельного двухполюсника:
 (1.53)
(1.53)
Таким образом, теория электрических цепей позволяет корректно учитывать в своих сравнительно простых феноменологических моделях процессы, протекающие в диэлектриках, находящихся в постоянном или переменном электрическом поле. Однако определяемые при этом параметры и соотношения между ними имеют сравнительно простой вид только при условии, что комплексное сопротивление и комплексная проводимость подчиняются линейным законам и цепи являются пассивными (инвариантными ко времени), т.е. их свойства не изменяются за период проведения одного измерения.
III.2.3. Пьезоэлектрические эффекты в полярных диэлектриках (сегнето- или ферроэлектрики).
Пьезоэффекты являются наиболее важными и распространенными электромеханическими эффектами, проявляющимися в полярных диэлектриках. Они связаны с возникновением электрического момента (поляризацией) при деформировании диэлектрика в отсутствие электрического поля (прямой пьезоэффект) или деформации и напряжения при приложении внешнего электрического поля (обратный пьезоэффект)(Рис.1.):

Рис.1. Схема обратного пьезоэффекта во внешнем электрическом поле
Обобщенное термодинамическое описание пьезоэффектов как совокупности взаимосвязанных механических и электрических явлений в полярных диэлектриках базируется на фундаментальном уравнении Гиббса в выражении для основной экстенсивной термодинамической функции состояния (внутренней энергии U)через основные экстенсивные независимые переменные: энтропиюS, объем V, геометрический линейный размер δ и напряженность электрического поля Е:  , где р – давление, σ - механическое напряжение, D - электрическая индукция. Преобразование фундаментального уравнения Гиббса с заменой двух экстенсивных независимых переменных (энтропии и объема), которые в экспериментах с твердыми телами трудно регулировать или поддерживать постоянными, на легко регулируемые интенсивные независимые переменные (температуру, механическое напряжение и напряженность электрического поля) дает уравнение для свободной энергии Гиббса в дифференциальной форме:
, где р – давление, σ - механическое напряжение, D - электрическая индукция. Преобразование фундаментального уравнения Гиббса с заменой двух экстенсивных независимых переменных (энтропии и объема), которые в экспериментах с твердыми телами трудно регулировать или поддерживать постоянными, на легко регулируемые интенсивные независимые переменные (температуру, механическое напряжение и напряженность электрического поля) дает уравнение для свободной энергии Гиббса в дифференциальной форме:  . Оно получено при условии, что давление и состав диэлектрика постоянны, работа, произведенная механическим напряжением и электрическим полем в системе, считается отрицательной и взята со знаком «минус», а также без учета работы против внешнего давления из-за ее малости при нормальном давлении р. При постоянной температуре это уравнение имеет вид:
. Оно получено при условии, что давление и состав диэлектрика постоянны, работа, произведенная механическим напряжением и электрическим полем в системе, считается отрицательной и взята со знаком «минус», а также без учета работы против внешнего давления из-за ее малости при нормальном давлении р. При постоянной температуре это уравнение имеет вид: 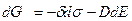 . Первые частные производные свободной энергии по независимым экстенсивным переменным σ и Е дают эквивалентные им механический и электрический параметры (деформацию δ и индукцию D соответственно), т.е. уравнения механического и электрического состояния:
. Первые частные производные свободной энергии по независимым экстенсивным переменным σ и Е дают эквивалентные им механический и электрический параметры (деформацию δ и индукцию D соответственно), т.е. уравнения механического и электрического состояния: 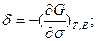
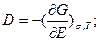
 . Вторые частные производные свободной энергии по этим переменным дают возможность определять другие параметры, связывающие электрические и механические эффекты (см.ниже).
. Вторые частные производные свободной энергии по этим переменным дают возможность определять другие параметры, связывающие электрические и механические эффекты (см.ниже).
Приведенное уравнение для свободной энергии содержит минимальное количество (две) независимых переменных как обобщенных термодинамических сил (σ и Е) и связанных с ними обобщенных реакций на эти силы (термодинамических координат δ и D) из девяти механических и электрических величин: шести механических, т.к. напряжение и деформации являются тензорами второго ранга и трех электрических – компонентов векторов напряженности и индукции. Учитывая векторную природу механических и электрических эффектов с помощью термодинамических соотношений можно получить обобщенные характеристики этих эффектов в полярных диэлектриках. Так, раскладывая выражения для первых производных свободной энергии по независимым экстенсивным переменным σ и Е в ряд вблизи некоторого начального состояния диэлектрика (при постоянных температуре, давлении и составе) и ограничиваясь только линейными членами разложения, можно описать всю совокупность механических и электрических эффектов с учетом векторной природы их параметров:
- деформации под действием механического напряжения (упругая деформация) и электрического поля (обратный пьезоэлектрический эффект) соответственно: 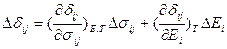 ;
;
- электрической индукции (поляризации) под действием механического напряжения (прямой пьезоэффект) и внешнего электрического поля (спонтанная поляризация) соответственно:  .
.
При описании параметров, характеризующих пьезоэффекты в полярных диэлектриках, полагают, что σ и Е связаны с δ и D линейными соотношениями, взятыми из теории упругости (σ =Мδ) и электродинамики (материальное уравнение Максвелла:D=ε0Е+Р) соответственно, где М – модуль упругости, а Р - диэлектрическая поляризация вещества, ε0 -диэлектрическая постоянная вакуума (e0=8,85∙10-12Ф/м). В случаепрямого пьезоэффекта, т.е. появления электрической поляризации внутри диэлектрика под влиянием механических напряжений или деформаций, в отсутствие внешнего электрического поля и при постоянных давлении, температуре и составе диэлектрика полагают также линейную зависимость между компонентами векторов механических напряжений σ или деформаций δ и вызываемой ими электрической поляризации Р: Р=dσ и Р=еδ соответственно, где коэффициенты пропорциональности представляют собой пьезоэлектрические константы: пьезмодуль d и пьзоконстанту деформации е, связанные между собой через модуль упругости М пьезоэлектрика (d=M/eили е=Мd) и являющиеся соответствующими частными производными Р по σ и δ:  .
.
В случае обратного пьезоэффекта, т.е. деформации образца или возникновение напряжений в нем под действием внешнего электрического поля, в отсутствие начального (остаточного) механического напряжения или деформации при постоянных давлении, температуре и составе диэлектрика общая его поляризация во внешнем электрическом поле определяется только его индуцированной (наведенной) поляризацией, зависящей от напряженности электрического поля и свойств диэлектрика:Р=χε0Е, где: c - диэлектрическая восприимчивость вещества (χ=ε-1,где ε – относительная диэлектрическая проницаемость диэлектрика), а электрическая индукция будет равна: D=ε0Е+Р=ε0εЕ. При наличии остаточной поляризации (Р0), как например в случае сегнето- или ферроэлектриков (см. ниже), общая электрическая индукция и поляризация описываются соотношениями: D=ε0εЕ+Р0 и Р=χε0Е+Р0. При этом также полагают линейную зависимость между компонентами вектора электрической поляризации Р и вызываемых ею механических напряжений σ или деформаций δ: Р=dσ и Р=еδ соответственно, а пьезмодуль d и пьзоконстанта деформации е определяются как частные производные δ и σ по Е: 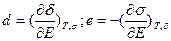 . При одновременном наличии механического напряжения σ или деформации δ и внешнего электрического поля при постоянных температуре, давлении и составе общая поляризация и электрическая индукция диэлектрика описываются через пьезомодуль и пьезоэлектрическую константу деформации соотношениями: Р=χε0Е+Р0+dσ=χε0Е+Р0+eδ; D=ε0εЕ+Р0+dσ=ε0εЕ+Р0+eδ. Во всех случаях поляризация диэлектриков связана с протеканием трех основных процессов (Рис.2): деформирования электронных облаков (электронная поляризация), смещения ионов (ионная поляризация) и ориентация полярных групп, звеньев или молекул (дипольная поляризация).
. При одновременном наличии механического напряжения σ или деформации δ и внешнего электрического поля при постоянных температуре, давлении и составе общая поляризация и электрическая индукция диэлектрика описываются через пьезомодуль и пьезоэлектрическую константу деформации соотношениями: Р=χε0Е+Р0+dσ=χε0Е+Р0+eδ; D=ε0εЕ+Р0+dσ=ε0εЕ+Р0+eδ. Во всех случаях поляризация диэлектриков связана с протеканием трех основных процессов (Рис.2): деформирования электронных облаков (электронная поляризация), смещения ионов (ионная поляризация) и ориентация полярных групп, звеньев или молекул (дипольная поляризация).

а) б) в)
Рис. 2. Схемы электронной (а), ионной (б) и дипольной (в) поляризаций
Вследствие векторной природы механических и электрических параметров прямой и обратный пьезоэффекты характеризуются, в зависимости от группы симметрии и пьезоэлектрической текстуры диэлектрика, различным набором (матрицей) пьезоэлектрических констант, описывающих связь величины приложенного механического напряжения или деформации и возникающего электрического поля или приложенного электрического поля и возникающую механическую деформацию или напряжение в различных направлениях. Так, удлинение материала в одном направлении вызывает сокращение его поперечных размеров, а прикладываемое электрическое поле способно вызывать не только растягивающие или сжимающие, но и сдвиговые деформации. В общем случае при заданном направлении вектора электрического поля Е и электрической индукции или интенсивности поляризации (D или P) диэлектрики могут характеризоваться 18 независимыми пьезоэлектрическими константами. Однако, вследствие симметрии структуры пьезодиэлектрика, одни из них могут быть равны нулю, другие эквивалентны, что значительно уменьшает число независимых констант. При описании пьезоэффектов в трехосной системе координат x,y,z или 1,2,3 направление вектора электрического поля Е и электрической индукции D обычно выбирается вдоль оси z или 3. Тогда константа dzz или d33 связывает электрическое поле и индукцию (поляризацию) в направлении оси z или 3 c величиной создаваемой в этом же направлении деформацией, а константа dzх или d31 связывает электрическое поле и индукцию (поляризацию) в направлении z или 3 и деформацию в ортогональном направлении х или 1. На практике константы dzz или d33 и dzх или d31 имеют наибольшее значение.
В самом общем виде пьезоэлектрические константы, или коэффициенты d и е, с учетом направлений по осям,могут бытьопределены как вторые частные производные свободной энергии диэлектрика или первые частные производные индукции (поляризации Р) по механическому напряжению, деформации, напряженности электрического поля и температуре или деформации по напряженности электрического поля соответственно:  ;
; 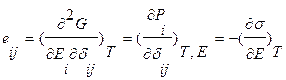 .
.
Обобщенными характеристиками, определяющими связь между их упругими и диэлектрическими свойствами и пьезоконстантами диэлектриков являются коэффициенты пьезочувтвительности g и электромеханической связи k: g=d/εε0; k=d2M/ εε0 соответственно. Так, чувствительность пьезопластины толщиной h равна gh ивыражается в мкВ/Па.
Наиболее сильными пьезоэффектами и, соответственно, наиболее важным классом пьезоэлектриков являются сегнетоэлектрики (СЭ), обычно называемые в иностранной литературе ферроэлектриками (ФЭ). При этом все сегнетоэлектрики являются пьезоэлектриками, но не все пьезоэлектрики являются сегнетоэлектриками. Сегнето- или ферроэлектрики представляют собой кристаллические сильно полярные диэлектрики или полупроводники, обладающие в определенном диапазоне температур способностью к спонтанной поляризации не только в присутствии, но и в отсутствии внешнего электрического поля, т.е. к возникновению остаточной поляризации - образованию связанного поверхностного заряда и соответствующего электрического момента (макроскопического диполя). В кристаллах таких диэлектриков отсутствует центр симметрии в упорядочении ионов или диполей. При наличии подвижных носителей зарядов (ионов, свободных электронов или «дырок») их движение к противоположно заряженным связанным зарядам может приводить к экранированию спонтанной поляризации и исчезновению остаточного электрического момента, который способен вновь восстанавливаться при воздействии на кристалл механического напряжения или электрического поля.
Проявление сегнето- или ферроэлектрического эффекта (СЭЭ или ФЭЭ) в кристаллах сегнетоэлектриков обусловлено структурным фазовым переходом 1-го или, чаще, 2-го рода с искажением структуры (понижением порядка симметрии или увеличением параметра порядка) кристалла при понижении температуры с переходом из неполяризованного (параэлектрического) состояния, или фазы (ПЭС) в поляризованное (сегнето- или ферроэлектрическое) состояние, или фазу (СЭС, или ФЭС). В большинстве случаев это искажение такое же, как при воздействии внешнего электрического поля на кристалл в параэлектрическом состоянии. Такие СЭ называются собственными. В некоторых случаях остаточная поляризация возникает как вторичный эффект структурного превращения, не связанного непосредственно с поляризацией, и не может быть вызвана электрическим полем. Такие СЭ называются несобственными.
Как правило, переход в СЭС непосредственно из ПЭС происходит как фазовый переход 2-го рода со сравнительно малыми изменениями структуры. Эти фазы в этом случае называют соразмерными. Если между ПЭС и СЭС возникает промежуточная фаза с особыми свойствами, то такая фаза называется несоразмерной. Переход в СЭС непосредственно из ПЭС сопровождается резким возрастанием вектора поляризации и повышением диэлектрической проницаемости диэлектрика, поэтому на спонтанную и остаточную поляризацию при таком переходе могут сильно влиять различные внешние воздействия: электрическое поле, механические воздействия, характер изменения температуры и др. Описание свойств собственных СЭ в области фазового перехода ПЭС/СЭС с соразмерными фазами (критической температуры Тк) базируется на теории Ландау-Гинзбурга, в соответствие с которой термодинамический потенциал (свободная энергия) определяется параметром порядка η, являющимся внутренней переменной, характеризующей изменение пространственной симметрии кристалла. При Т большей или равной Тк η =0, а при Т<Тк η ≠0. Вблизи Тк свободная энергия разлагается в ряд по степеням η. При наличии механического напряжения и поляризации первые члены такого ряда для свободной энергии равновесного сегнетоэлектрического кристалла записыватся в виде:  , где βТ – объемная сжимаемость, χ – электрическая восприимчивость. При Т=Тк резко возрастает величина вектора поляризации, а диэлектрическая восприимчивость и относительная диэлектрическая проницаемость вдоль полярного направления проходят точку сингулярности (теоретически с разрывом функции) в соответствие с законом Кюри-Вейса: χzz =A/Т-Тк и εzz=C/Т-Тк, где А, С – константы, а теплоемкость претерпевает скачок. Поскольку экспериментальные данные несколько расходятся с теорией Ландау-Гинзбурга, современные теории таких переходов базируются на представлениях теории перколяции об образовании, росте и агрегировании кластеров - флуктуаций ориентации локальных электрических моментов или диполей, с возникновением в точке фазового перехода 2-го рода непрерывного (перколяционного) кластера фрактальной природы. Мощность такого кластера, характеризуемая вектором поляризации, описывается степенной функцией удаленности температуры Т от Тк (скейлинговым соотношением):
, где βТ – объемная сжимаемость, χ – электрическая восприимчивость. При Т=Тк резко возрастает величина вектора поляризации, а диэлектрическая восприимчивость и относительная диэлектрическая проницаемость вдоль полярного направления проходят точку сингулярности (теоретически с разрывом функции) в соответствие с законом Кюри-Вейса: χzz =A/Т-Тк и εzz=C/Т-Тк, где А, С – константы, а теплоемкость претерпевает скачок. Поскольку экспериментальные данные несколько расходятся с теорией Ландау-Гинзбурга, современные теории таких переходов базируются на представлениях теории перколяции об образовании, росте и агрегировании кластеров - флуктуаций ориентации локальных электрических моментов или диполей, с возникновением в точке фазового перехода 2-го рода непрерывного (перколяционного) кластера фрактальной природы. Мощность такого кластера, характеризуемая вектором поляризации, описывается степенной функцией удаленности температуры Т от Тк (скейлинговым соотношением):  , где β является универсальным показателем степени (критическим индексом), величина которого зависит только от размерности пространства d. При d=3 в соответствие с моделью Изинга β =0,32. Другими важными показателями структуры и свойств такого кластера служат корреляционная длина (мера параметра порядка) ξ и диэлектрическая восприимчивость (характерный размер) χ, температурные зависимости которых вблизи точки перехода также описываются скейлинговыми соотношениями с универсальными критическими индексами υ и γ:
, где β является универсальным показателем степени (критическим индексом), величина которого зависит только от размерности пространства d. При d=3 в соответствие с моделью Изинга β =0,32. Другими важными показателями структуры и свойств такого кластера служат корреляционная длина (мера параметра порядка) ξ и диэлектрическая восприимчивость (характерный размер) χ, температурные зависимости которых вблизи точки перехода также описываются скейлинговыми соотношениями с универсальными критическими индексами υ и γ:  и
и  , равными в модели Изинга 0,63 и 1.25 соответственно. Все критические индексы связаны между собой через размерность пространства единым соотношением (гиперскейлингом): dυ=γ+2β. Скейлинг и гиперскейлинг вблизи температуры фазового перехода второго рода (критической точки) обусловлен свойствами масштабной инвариантности перколяционных фрактальных кластеров вблизи порога перколяции.
, равными в модели Изинга 0,63 и 1.25 соответственно. Все критические индексы связаны между собой через размерность пространства единым соотношением (гиперскейлингом): dυ=γ+2β. Скейлинг и гиперскейлинг вблизи температуры фазового перехода второго рода (критической точки) обусловлен свойствами масштабной инвариантности перколяционных фрактальных кластеров вблизи порога перколяции.
Термодинамический анализ сегнетоэлектрического (поляризованного) состояния СЭ показывает, что равновесные значения поляризации, отвечающие минимуму свободной энергии, могут быть положительными или отрицательными, т.е. в СЭС возможно несколько эквивалентных направлений ориентации вектора поляризации – по два вдоль каждой оси поляризации, или, что тоже самое, возможно несколько областей ориентации локальных электрических моментов или диполей. Это обусловливает возможность самопроизвольного разбиения сегнетоэлектрического кристалла на домены - области с различной ориентацией вектора поляризации, форма и характер распределения которых и границы (стенки) между ними (доменная структура) в условиях равновесия определяется требованиями минимума свободной энергии. В идеальном СЭС при полной компенсации однородных по объему электрических и механических полей, т.е. в электрически закороченном (противоположные электроды замкнуты на себя) и механически свободном состоянии разбиение на домены энергетически невыгодно, т.к. образование доменных стенок дает положительный вклад в свободную энергию. В обычно электрически незакороченных СЭ разбиение на домены энергетически выгодно, т.к. оно сопровождается резким уменьшением энергии дальнодействующего электростатического взаимодействия между различными частями кристалла, компенсирующим энергию образования доменных стенок (Рис.3).
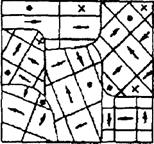
Рис. 3. Схематическое изображение доменов тетрагональной модификации титана бария (ВаTiO3). Стрелкой указаны направления вектора поляризации
Большое влияние на характер образующейся доменной структуры оказывает предыстория материала, в первую очередь условия прохождения через точку Кюри (скорость охлаждения, ориентирующее воздействие внешнего электрического или механического поля), а также дефекты его структуры, экранирование электрического поля за счет перераспределения свободных носителей зарядов и др.
Внешнее электрическое поле может оказывать существенное влияние не только на формирование доменной структуры СЭ при прохождении через точку Кюри, но и изменять ее характер в сформированном состоянии при Т <Тк. Под действием внешнего электрического поля доменные стенки могут смещаться, а размеры и объем доменов, ориентированных по полю, могут возрастать за счет доменов, ориентированных против поля. Перестройка доменной структуры кристалла СЭ под действием электрического поля определяет характер зависимости вектора общей поляризации от напряженности поля, имеющей вид петли гистерезиса (Рис.4). В сильном поле кристалл может переходить

Рис. 4. Зависимость поляризации Р (а) и диэлектрической проницаемости ε (б) сегнетоэлектрика от напряженности поля Е
практически в однодоменное состояние. При последующем уменьшении напряженности поля до нуля поляризация отлична от нуля (Рост) и обращается в нуль только при приложении достаточно большого поля противоположного знака –Ес (коэрцитивного поля или коэрцитивной силы). Величина Ес определяет «жесткость» СЭ и зависит от подвижности доменных стенок. Резкое изменение поляризации СЭ под действием электрического поля, связанное в первую очередь со смещением доменных стенок, обусловливает высокие значения их диэлектрической проницаемости и ее зависимость от напряженности поля, особенно вблизи Тк .. Этим объясняется тот факт, что все СЭ в СЭС являются пьезоэлектриками с высокими коэффициентами, связывающими их деформации с электрическим полем. Этим же объясняются высокие значения пироэлектрических констант. Однако, высокие значения диэлектрической проницаемости СЭ могут приводить к сравнительно низким значениям коэффициентов пьезочувствительности и электромеханической связи (g и k соответственно): g=d/εε0; k=d2M/ εε0.
В экспериментах для расчета силы и деформации, возникающих при приложении электрического напряжения U к цилиндрическому образцу сегнетоэлектрика площадью А и длиной l в соответствие со схемой:
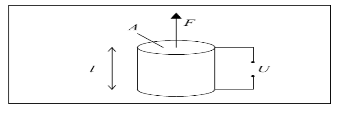
используются соотношения:  ;(7) и
;(7) и  (8), где:
(8), где:  ,
, 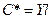 , δ0 –деформация в направлении силы F, U – напряжение, Y – модуль Юнга, k – коэффициент электромеханической связи, А – площадь сечения образца.
, δ0 –деформация в направлении силы F, U – напряжение, Y – модуль Юнга, k – коэффициент электромеханической связи, А – площадь сечения образца.
В случае типичного сегнетоэлектрика (ε=3500, k=0,74, Y=50 ГПа, А=1см2 и l=20 мм) для создания силы F=50 Н необходимо напряжение 343 В. Возникающая при этом деформация δ0 = 0,2 мкм.
При оценке силы в трансверасльном направлении (перпендикулярно l) и при сдвиге для прямоугольного сечения (l – высота, b – длина, t – ширина):  ;
; 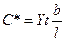 ;
;  ;
;  соответственно (G- модуль упругости при .сдвиге).
соответственно (G- модуль упругости при .сдвиге).
Для повышения величины пъезоэлектрического эффекта и, соответственно, эффективности пьезоэлектрических сенсоров или актюаторов используются не только однослойные (моноблочные) пьезоэлементы, но и многослойные, или пакетные, чаще всего, двухслойные (биморфные) элементы (биморфы), состоящие из адгезионно связанных консольно закрепленных тонких слоев пьезоматериала одного или разных типов с упрочняющей металлической прослойкой между ними или без нее. Биморф, состоящий из двух слоев, направление поляризации которых одинаковы, называют параллельными, а противоположны – последовательным, причем в случае параллельного биморфа развиваемое усилие, при прочих равных условиях, в два раза больше, чем в случае последовательного. Биморф может работать как с использованием прямого пьезоэлектрического эффекта (в режиме сенсора или генератора, не требующего внешнего источника питания), так и с использованием обратного пьезоэлектрического эффекта (в режиме пьезоэлектрического актюатора, требующего для возбуждения наличия внешнего сигнала или источника питания). При работе в режиме актюатора в последовательном биморфе слои электрически соединены последовательно, причем слой с положительной полярностью находится под воздействием положительного напряжения и вследствие обратного пьезоэффекта удлиняется, а пластина с отрицательной полярностью препятствует этому удлинению, вызывая изгиб биморфа. Так как последняя находится под напряжением, противоположным напряжению поляризации, то существует опасность деполяризации. Для исключения этого эффекта обе пластины необходимо возбуждать в направлении поляризации с подачей напряжения смещения. В случае параллельного биморфа внешние электроды, находящиеся на поверхности слоев, подключаются к одному выводу, а центральный электрод, находящийся между слоями, подключается к другому выводу. Оба типа биморфов обладают свойствами конденсаторов, и после снятия напряжения накопленная в них энергия высвобождается довольно медленно. Быстродействие биморфа определяется значением статической выходной емкости, величина которой зависит от геометрических параметров и диэлектрических свойств пьезоэлектрика. Для увеличения быстродействия требуется включение в электрическую схему резисторов.