 |
|
Домашнее задание № 13
ТЕМА 13.
ПРОИЗВОДНАЯ ФУНКЦИИ.
План:
- Вычисление производных с применением табличных значений.
- Дифференцируемость функции. Правила дифференцирования
- Вычисление производной сложной функции
Литература
- Баврин, И.И.Высшая математика: учеб. для студ. естественно-научных спец. пед. вузов/ И.И. Баврин. - М.: Издательский центр «Академия»., 2004.– 616 с.
- Баврин, И.И. Математический анализ: учебник./ И.И. Баврин, М.: Высш. шк., 2006 – 327 с.
- Данко П. Е. Высшая математика в упражнениях и задачах: учеб. пособ. для вузов. В 2 ч. Ч. 1. / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. – М.: Мир и Образование, 2003. – 304 с.
Теоретический материал
Производной данной функции y = f(x) в точке x0 называется предел отношения приращения функции Δy к приращению аргумента Δx, когда последнее произвольным образом стремится к нулю.
Для непосредственного нахождения производной по определению можно применить следующее практическое правило:
1. Придать x приращение Δx и найти наращенное значение функции f(x + Δx).
2. Найти приращение функции Δy = f(x + Δx) – f(x).
3. Составить отношение 
и найти предел этого отношения при Δx∞0.
Примеры.
1. Найти производную функции y = x2
а) в произвольной точке;
б) в точке x= 2.
а)
1. f(x + Δx) = (x + Δx)2;
2. Δy = (x + Δx)2 – x2=2xΔx– x2;
3. 
.
б) f '(2) = 4
ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. Пусть u=u(x),v=v(x) – две дифференцируемые функции от переменной x.
.
(справедлива для любого конечного числа слагаемых).
.
.
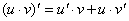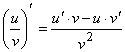а) 
.
б)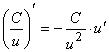 
.
ТЕОРЕМА О ПРОИЗВОДНОЙ СЛОЖНОЙ ФУНКЦИИ
Пусть y = f(u), а u= u(x). Получаем функцию y, зависящую от аргумента x: y = f(u(x)). Последняя функция называется функцией от функции или сложной функцией.
Теорема. Если функция u= u(x) имеет в некоторой точке x0 производную 
и принимает в этой точке значение u0 = u(x0), а функция y= f(u) имеет в точке u0 производную y 'u= f '(u0), то сложная функция y = f(u(x)) в указанной точке x0 тоже имеет производную, которая равна y 'x= f '(u0)·u '(x0), где вместо u должно быть подставлено выражение u= u(x).
Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x.
Задания для занятия
1. Найдите производную следующих функций:
| 1.у=3х-4х4 | 2. у=8-х2 |
3. у= 
| 4. y= 
|
5. у= 
| 6. у=(4x+1)2 |
7. у=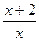 
| 8. у=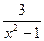 
|
9. у= 
| 10. у= 
|
11.
| 12.
|
| 13.y=x2(2x-1) | 14.y=(x3+3)(4x2-5) |
| 15. у=(х-5)4(х+3)5 | 16. у=(x2-4x+8) ex/2 |
| 17. у=x2 2x | 18. у=ex ln x |
| 19. у=(x-2) arcsin x + 2x arccos x | 20. у= 
|
21. у=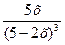 
| 22. у=  
|
23. у= 
| 24. у= 
|
| 25. у=sin 3 x | 26. у=sin x 3 |
| 27. у=tg 4(x2+1) | 28. у=ln tg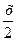 
|
29.
| 30. 
|
31.
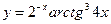
| 32.
|
33. 
| 34.
|
2. Найдите производную второго порядка следующих функций:
| 1. у=e-x | 2. у=sin 2x |
| 3. у=cos x2 | 4. у=ctg x |
5. у= 
| 6. y=ln (2x-3) |
3. Найдите производную третьего порядка следующих функций:
| 1. у=хe-x | 2. у=х 2 sin x |
| 3. у=e x cos x | 4. у= x3 2x |
| 5. у=arctg (x/2) | 6. y=x ln x |
Домашнее задание № 13
1. у= 
| 2. y=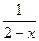 
|
| 3. у=arcsin x +6x+5arccos x | 4. у=(3-7x)6 |
5. у= 
| 6. у= 
|
7. у=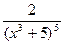 
| 8. у=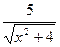 
|
9.
| 10. 
|
| 11.y=x2 log 3x | 12.y= 
|
| 13. у=(4х-1)2(х-2)4 | 14. у=(x2-6x-4) e-3x |
| 15. у=arccos (1-2x) | 16. у=sin (2x) |
17. у= 
| 18. у= 
|
| 19. у=sin 2 x3 | 20. у= 
|
| 21. у=ctg 3(x3-1) | 22. у=tg sin cos x 2 |
23. 
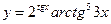
| 24. у=51/cos x |
2. Найдите производную второго порядка следующих функций:
1. у=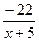 
| 2. у=cos 3x |
| 3. у=tg x |