 |
|
Примеры исследования функций с помощью производных и построение графиков.
Пример 1.Исследовать функцию у = 
и построить ее график.
Решение. 1) Функция у = 
определена всюду, кроме точки x=1. Отсюда область определения её: (–¥,1) È(1,+¥) .
2) x=1 – точка разрыва функции.
Исследуем поведение функции в граничных точках области определения:
f (x) = 
= +¥,
f (x) = = +¥, так как при х®1 знаменатель дроби является положительной бесконечно малой.
= 
= 
=+¥;
= 
= =–¥.
3) Найдем точки пересечения графика функции с осями координат. При х = 0 получаем у = 0, т.е. график функции пересекает координатные оси в точке O(0,0).
4) Прямая х = 1 является вертикальной асимптотой графика функции.
Найдем наклонные асимптоты:
k= 
= 
= 
= 
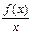= 1, т.е. k =1;
b = ( f (x)– kx ) = 
= 
= = 
= 
= 
= = 
= 
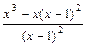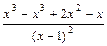=2,
т.е. b=2. Имеем уравнение правой наклонной асимптоты y = x+2.
Легко убедиться, что при x ®–¥ k и b имеют те же значения, т.е. уравнение левой наклонной асимптоты такое же y = x+2.
5) Найдем производную функции: y' = 
=
= 
= 
= 
.
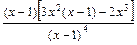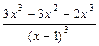Приравнивая y' к нулю, получим x3–3x2=0, откуда имеем критические точки x1=0, x2=3. Для исследования знака производной в интервале (–¥;0), (0;3) и (3; +¥) на числовой оси отметим точки x=0, x=3 и х=1.
Определим знаки y' = 
в указанных интервалах.
Таким образом, в интервале (–¥;1) функция возрастает, в интервале (1,3) – убывает, в интервале (3,+ ¥) она возрастает. В точке x=3 функция имеет минимум: f (3) = 
= 
= 6,75.
6) Найдем вторую производную:
y''= 
= 
= = 
=
= 
= 
, y''=0 при x=0. Так как знаменатель дроби (x–1)4>0 всегда (кроме x=1), то знак второй производной зависит лишь от числителя. При x<0 y''<0, при x>0 y''>0.
Точка x=0 является точкой перегиба. При x<0 кривая направлена выпуклостью вверх, так как y''<0, а при x>0 – выпуклостью вниз. В точке перегиба f (x) имеет значение f (0)=0.
Результаты наших исследований объединим в таблицу.
| x | (–¥,0) | (0,1) | (1,3) | (3,+¥) | |||
| y' | + | + | – | + | |||
| y'' | – | + | + | + | |||
| y | äÇ | точка перегиба | Èä | не суще– ствует | æÈ | min | Èä |
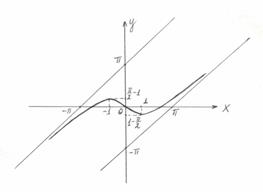
Строим график функции, предварительно построив асимптоты и отметив точки минимума, перегиба и пересечения графика с осями координат.
Пример 2. Исследовать функцию 
и построить ее график.
1. Область определения: 
.
2. Пусть 
, тогда y=0.Пусть y=0, тогда 
- решить уравнение точно не удается.
Найдена точка 
пересечения графика с осями координат.
3. 
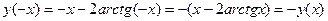– функция нечетная.
4. Функция непрерывна во всей области определения. Вертикальных асимптот нет.
5. Невертикальные асимптоты.
.
,
.
.
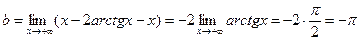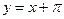- асимптота при 
, 
- асимптота при
.
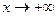6. 
; 
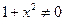при 
.
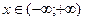, если 
, откуда 
и 
- критические точки. Нанесем критические точки на числовую прямую и определим знаки производной в образовавшихся интервалах.
 |
+ - +
-1 1
На интервалах 
и 
функция возрастает, а на интервале 
– убывает.
, 
7. 
; 
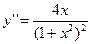, если 
, откуда - критическая точка второго порядка. Нанесем ее на числовую прямую и определим знаки второй производной в образовавшихся интервалах.
 |
- +
На интервале 
график выпуклый, а на интервале 
- выгнутый. - точка перегиба.
8. 
, 
.
