 |
|
ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК БОРТОВОЙ КАЧКИ КОРАБЛЯ ПРИ ОБРАБОТКЕ ЗАПИСЕЙ СВОБОДНЫХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
В результате исследования бортовой качки моделей кораблей на тихой воде методом свободных затухающих колебаний можно определить период и частоту собственных колебаний 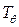 и
и  , безразмерный коэффициент затухания
, безразмерный коэффициент затухания  и коэффициент присоединенной массы
и коэффициент присоединенной массы 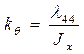 .
.
Перед обработкой осциллограммы свободных затухающих колебаний необходимо определить тарировочный (градуировочный) коэффициент  , устанавливающий зависимость между углами наклонения и их размером в миллиметрах на ленте регистрирующего осциллографа. Определение коэф-фициента
, устанавливающий зависимость между углами наклонения и их размером в миллиметрах на ленте регистрирующего осциллографа. Определение коэф-фициента  производится на основании тарировочного графика, построен-ного по характерной тарировочной записи (рис. 6.8).
производится на основании тарировочного графика, построен-ного по характерной тарировочной записи (рис. 6.8).
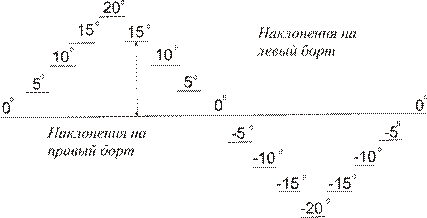
Рис. 6.8 Запись тарировки гировертикали
Для построения тарировочного графика необходимо назаписи измерить отклонения lосц. в миллиметрах от нулевой линии ( 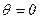 ) при соответствую-щих значениях угла крена q. Затем по полученным значениям надо построить зависимость lосц = f(q). Получаемая зависимость всегда близка к линейной, поэтому ее можно аппроксимировать прямой линией, проходящей через начало координат (рис. 6.9). Уравнение этой прямой имеет вид:
) при соответствую-щих значениях угла крена q. Затем по полученным значениям надо построить зависимость lосц = f(q). Получаемая зависимость всегда близка к линейной, поэтому ее можно аппроксимировать прямой линией, проходящей через начало координат (рис. 6.9). Уравнение этой прямой имеет вид:
 . (6.13)
. (6.13)
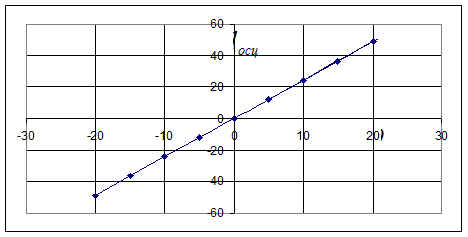 |
Рис. 6.9. Определение тарировочного коэффициента 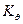
Чтобы рассчитать  , надо при фиксированном значении q на графике измерить соответствующее значение lосц и взять отношение
, надо при фиксированном значении q на графике измерить соответствующее значение lосц и взять отношение
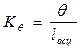 . (6.14)
. (6.14)
В приведенном на рис. 6.9 примере при q = 200 lосц = 48,8 мм. Тогда  = 0,41 град / мм.
= 0,41 град / мм.
Для определения периода 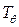 по осциллограмме выполняют следующее:
по осциллограмме выполняют следующее:
1) тщательно проводят огибающие кривые затухающих колебаний;
2) нумеруют через полпериода все амплитудные значения колебаний, кроме начального (рис. 6.10);
3) выделяют n полных колебаний и с помощью вертикальных линий, дающих отсечки времени (тонкие через 0,2 с, жирные – через 2 с) измеряют время Tn этих колебаний (рис.6.10). В рассматриваемом примере количество полных колебаний равно 9;
4) определяют собственный период бортовой качки и собственную частоту как
 ; (6.15)
; (6.15)
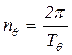 . (6.16)
. (6.16)
Для определения безразмерного коэффициента демпфирования  может быть использована одна из следующих формул:
может быть использована одна из следующих формул:
· формула С.Н. Благовещенского
 , (6.17)
, (6.17)
где
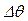 - разность двух соседних амплитуд;
- разность двух соседних амплитуд;
 - среднее арифметическое этих же амплитуд;
- среднее арифметическое этих же амплитуд;
· логарифмическая формула
 . (6.18)
. (6.18)
Расчет по формуле (6.17) проводится в табличной форме (табл. 6.1) в следующей последовательности:
1) на каждом размахе, начиная с первого снимаются в мм значения размаха liосц как расстояние по вертикали между огибающими (рис. 6.10) и заносятся во II столбец таблицы;
2) вычисляются qi , 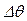 и
и 
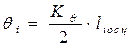 ; (6.19)
; (6.19)
 ; (6.20)
; (6.20)
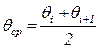 ; (6.21)
; (6.21)
3) по результатам вычислений 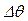 строится график
строится график 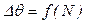 (N-номер размаха). Из-за некоторых погрешностей, имеющих место при проведении эксперимента и снятии liосц, значения
(N-номер размаха). Из-за некоторых погрешностей, имеющих место при проведении эксперимента и снятии liосц, значения 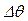 не ложатся на плавную кривую, в связи с чем необходимо провести графическую аппроксимацию зависимости
не ложатся на плавную кривую, в связи с чем необходимо провести графическую аппроксимацию зависимости 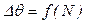 с помощью осредняющей плавной кривой. При этом осредняющая кривая должна убывать при увеличении N (рис. 6.11);
с помощью осредняющей плавной кривой. При этом осредняющая кривая должна убывать при увеличении N (рис. 6.11);
4) в Y столбец заносятся значения  , снятые с аппроксимирующей
, снятые с аппроксимирующей
кривой для каждого размаха (рис. 6.11);
4) в YI столбце вычисляются значения безразмерного коэффициента
демпфирования.

Рис. 6.10. Осциллограмма свободных затухающих колебаний

Рис. 6.11. Аппроксимация зависимости 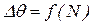
Таблица 6.1. Расчет безразмерного коэффициента затухания по формуле (6.17)
 N N
|  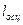
| 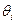
| 
| 
| 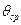
| 
|
| I | II | III | IY | Y | YI | YII |
| 15,58 | - | - | - | - | ||
| 14,76 | 0,82 | 0,94 | 15,17 | 0,0394 | ||
| 13,94 | 0,82 | 0,86 | 14,35 | 0,038 | ||
| 13,12 | 0,82 | 0,8 | 13,53 | 0,0376 | ||
| 12,505 | 0,615 | 0,76 | 12,8125 | 0,0377 | ||
| 11,685 | 0,82 | 0,68 | 12,095 | 0,0357 | ||
| 11,07 | 0,615 | 0,62 | 11,3775 | 0,03469 | ||
| 10,455 | 0,615 | 0,56 | 10,7625 | 0,03312 | ||
| 48,5 | 9,9425 | 0,5125 | 0,52 | 10,198 | 0,03246 | |
| 45,5 | 9,3275 | 0,615 | 0,48 | 9,635 | 0,0317 | |
| 42,5 | 8,7125 | 0,615 | 0,44 | 9,02 | 0,03105 | |
| 8,2 | 0,5125 | 0,41 | 8,456 | 0,0308 | ||
| 37,5 | 7,6875 | 0,5125 | 0,35 | 7,944 | 0,028 | |
| 35,5 | 7,2775 | 0,41 | 0,32 | 7,4825 | 0,0272 | |
| 6,97 | 0,3075 | 0,28 | 7,124 | 0,025 | ||
| 31,5 | 6,4575 | 0,5125 | 0,25 | 6,713 | 0,0237 | |
| 6,15 | 0,3075 | 0,22 | 6,303 | 0,022 | ||
| 5,945 | 0,205 | 0,19 | 6,047 | 0,02 | ||
| 28,5 | 5,8425 | 0,1025 | 0,18 | 5,89 | 0,0194 |
Расчет по коэффициента демпфирования по формуле (6.18) проводится следующим образом (табл. 6.2):
1) вычисляют 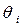 по формуле (6.19),
по формуле (6.19),  и
и 
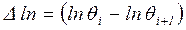 ; (6.23)
; (6.23)
2) строят графическую зависимость 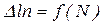 и проводят аппрокси-мирующую кривую (рис. 6.12);
и проводят аппрокси-мирующую кривую (рис. 6.12);
3) в YI столбец заносят значения  , снятые с аппроксимирующей кривой (рис. 6.12);
, снятые с аппроксимирующей кривой (рис. 6.12);
4) вычисляют значения безразмерного коэффициента демпфирования.
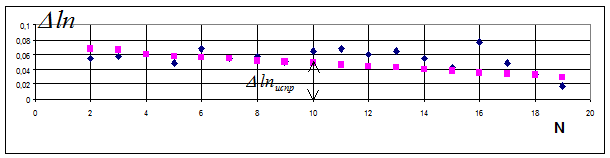
Рис. 6.12. Аппроксимация зависимости 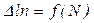
Таблица 6.2. Расчет безразмерного коэффициента затухания по формуле (6.18)

| 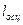 с с
| 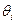
| 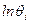
| 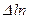
| 
| 
| 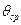
|
| I | II | III | IY | Y | YI | YII | YIII |
| 15,58 | 2,746 | - | - | - | - | ||
| 14,76 | 2,692 | 0,054 | 0,068 | 0,0433 | 15,17 | ||
| 13,94 | 2,635 | 0,057 | 0,066 | 0,042 | 14,35 | ||
| 13,12 | 2,574 | 0,061 | 0,06 | 0,038 | 13,53 | ||
| 12,505 | 2,526 | 0,048 | 0,058 | 0,0369 | 12,8125 | ||
| 11,685 | 2,458 | 0,068 | 0,056 | 0,0356 | 12,095 | ||
| 11,07 | 2,404 | 0,054 | 0,054 | 0,0343 | 11,3775 | ||
| 10,455 | 2,347 | 0,057 | 0,052 | 0,033 | 10,7625 | ||
| 48,5 | 9,9425 | 2,297 | 0,05 | 0,05 | 0,0318 | 10,198 | |
| 45,5 | 9,3275 | 2,233 | 0,064 | 0,048 | 0,0305 | 9,635 | |
| 42,5 | 8,7125 | 2,165 | 0,068 | 0,046 | 0,0292 | 9,02 | |
| 8,2 | 2,104 | 0,061 | 0,044 | 0,028 | 8,456 | ||
| 37,5 | 7,6875 | 2,0396 | 0,0644 | 0,042 | 0,0267 | 7,944 | |
| 35,5 | 7,2775 | 1,9847 | 0,0549 | 0,04 | 0,0254 | 7,4825 | |
| 6,97 | 1,9416 | 0,0431 | 0,038 | 0,024 | 7,124 | ||
| 31,5 | 6,4575 | 1,865 | 0,0766 | 0,036 | 0,0229 | 6,713 | |
| 6,15 | 1,816 | 0,049 | 0,034 | 0,0216 | 6,303 | ||
| 5,945 | 1,7825 | 0,0335 | 0,032 | 0,0203 | 6,047 | ||
| 28,5 | 5,8425 | 1,765 | 0,0175 | 0,03 | 0,019 | 5,89 |
Результаты вычисления безразмерного коэффициента демпфирования по каждой из формул представляются графически в виде зависимости 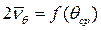 (рис. 6.13). Обычно результаты обработки по обеим формулам очень близки.
(рис. 6.13). Обычно результаты обработки по обеим формулам очень близки.

Рис. 6.13 Значения коэффициента затухания, полученные по формулам (6.17) и (6.18)
В практических расчетах качки иногда требуется знать коэффициент квадратичного сопротивления  . Для его определения используется сле-дующая формула:
. Для его определения используется сле-дующая формула:
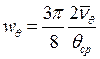 , (6.25)
, (6.25)
полученная из условия равенства работ линейного и квадратичного моментов сопротивления качке за четверть периода.
Для вычисления коэффициента присоединенной массы используется формула:
 . (6.26)
. (6.26)
Напоминаем, что
Jx - момент инерции массы корпуса;
D - весовое водоизмещение модели;
h0 - начальная метацентрическая высота модели;
 - замеренный по осциллограмме период.
- замеренный по осциллограмме период.