 |
|
Чвертьфінал (заочний етап )
Заочна робота
Учасника 28 Міжнародного чемпіонату
З розв’язування логічних математичних задач
Учня (учениці) _______ класу
Школи _______________________________________
Назва населеного пункту (область, район)________
______________________________________________
Прізвище, ім’я, по-батькові_____________________
Дата, місяць і рік народження учасника_________
Прізвище, ім’я, по-батькові учителя математики
______________________________________________
Умови завдань чвертьфіналу (заочного етапу) 28 Міжнародного чемпіонату з розв’язування логічних математичних задач подано у додатку.
Додаток
Міжнародний чемпіонат з розв’язування логічних математичних задач.
Чвертьфінал (заочний етап )
· У дідуся Івана в гаманці 10 монет: 5 – вартістю 1 гривня та 5 монет вартістю 50 коп. Всі монети він роздав Марічці, Миколці та Михайлику, причому всі діти отримали однакову суму грошей. Марічка та Миколка отримали однакову кількість монет. Скільки монет вартістю 1 гривня і скільки монет вартістю 50 коп. отримав Михайлик?
· Позначаючи день місяця (від 01 до 31), використовують дві цифри. Дві цифри використовують також для позначення місяця (від 01 до12). Скільки дат за період від першого січня (01.01.) до тридцять першого грудня (31.12) можна записати ( в будь – якому порядку), використовуючи цифри 2, 0, 1, 4?
· Є п’ять гирьок. Чотири з них мають відповідно маси 2 кг, 3 кг, 5 кг, 10кг. Всі гирьки розмістили на терезах так, що терези виявились у рівновазі. Знайдіть масу п’ятої гирьки, якщо відомо, що її маса така ж, як однієї з чотирьох інших гирьок.
· Піраміду склали з фігурок так, як показано на малюнку. По піраміді кидають м’ячем. Якщо м’яч попадає по фігурці, то вона падає і разом з нею падають всі ті фігурки, що розміщені вище неї і торкаються її, а також падають фігурки, розміщені вище фігурок, які торкаються фігурки, зачепленої м’ячем. ( Наприклад, якщо м’яч попав по фігурці №4, то падають фігурки №4, №7, №9, №10.) Набрані бали рахуються як сума номерів всіх фігурок, що впали. Богдан кинув м’ячем один раз і набрав 40 балів. Вкажіть номер фігурки, в яку він попав м’ячем.

· У Марічки є 4 браслети однакового діаметра. Коли вона розклала 3 браслети на столі, вони утворили сім фігурок, обмежених дугами кіл. (Дивись малюнок). Яку найбільшу кількість фігурок, обмежених дугами, зможе нарахувати Марічка, якщо покладе на стіл ще й четвертий браслет?

· На конкурсі молодих виконавців Іванна, Богдана, Світлана та Діана виконали декілька пісень. Кожна пісня виконувалась тріо (одночасно співали якихось три з чотирьох дівчат). Іванна виконала найменшу кількість пісень - 4. Діана виконала найбільшу кількість пісень - 8. Скільки всього пісень було виконано на конкурсі?
· В кружечки фігури, зображеної на малюнку, записано числа від 1 до 11. Сума чисел, записаних в кожних трьох або п’яти кружечках, вздовж п’яти прямих, зображених на малюнку, постійно дорівнює 22. Розставте числа (без повторень) від 4 до 10 так. щоб виконувались умови задачі.

· Михайлик написав трицифрове число. Остання цифра цього числа 5. Добуток цифри сотень і цифри десятків у 25 разів менший від написаного числа. Яке число написав Михайлик?
· Марічка має 5 бамбукових паличок, довжина кожної з яких відповідно дорівнює 2см, 3см, 4см, 5см, 6см. З трьох паличок можна скласти трикутник (дивись малюнок). Скільки різних трикутників може скласти Марічка з цих паличок?

· Перше число Назара дорівнює 7. Він підносить його до квадрату і отримує 49. Знаходить суму цифр цього числа і додає до неї 1. Отримує число 14 (4+9+1=14). Це друге число послідовності чисел Назара. Щоб знайти наступне число послідовності, Назар підносить до квадрату попереднє число послідовності і до суми цифр результату додає 1. Знайдіть сьоме число послідовності Назара.
· Серед студентів, які зібралися на вечірку, нараховується понад 40% хлопців і понад 50% дівчат. Вкажіть найменшу з можливих кількість студентів, що зібралися на вечірку.
· Цифри від 1 до 9 стилізовані та записані на п’яти прозорих пазлах (дивись малюнок). Пазли можна повертати, перевертати, та накладати один на одного. Складіть з пазлів таблицю 3 Х 3 так, щоб в її клітинках були записані всі цифри від 1 до 9, причому по одній цифрі в кожній клітинці.

· На малюнку зображено квадрат зі стороною 18см. На сторонах квадрата позначено їх середини. Знайдіть площу фігури, яка на малюнку зображена сірим кольором. Відповідь запишіть в кв. см. (Якщо потрібно, проведіть округлення до цілих).

· На аркуші А – 5 (14,8 см  21 см) Марічка накреслила два прямокутника, сторони кожного з яких дорівнюють цілому числу сантиметрів. Периметри прямокутників однакові, а площа другого в два рази більша, ніж площа першого. Знайдіть периметр кожного з цих прямокутників.
21 см) Марічка накреслила два прямокутника, сторони кожного з яких дорівнюють цілому числу сантиметрів. Периметри прямокутників однакові, а площа другого в два рази більша, ніж площа першого. Знайдіть периметр кожного з цих прямокутників.
· Якщо до числа 2014 додати добуток всіх його цифр, то одержимо 2014. Знайдіть інше число, сума якого з добутком всіх своїх цифр теж дорівнює 2014.
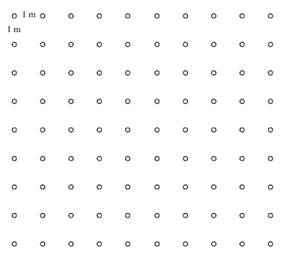
· На малюнку зображено квадратну сітку (сторона кожного квадратика 1 метр). Потрібно відгородити територію за допомогою двадцяти бар’єрів, довжина кожного з яких 5 метрів. Кінці кожного з бар’єрів можна ставити лише у вузлах сітки (на малюнку вузли позначено точками). Ділянку якої найбільшої площі можна відгородити? Відповідь запишіть в кв. м, округливши її до цілого числа.
· Дано трикутник. В середині нього розміщено три квадрати так, як показано на малюнку. Сторона кожного з трьох квадратів дорівнює 2,8 дм. Кут трикутника, що лежить навпроти його сторони, довжиною 8,4 дм, дорівнює 75 градусів. Знайдіть площу трикутника. Відповідь запишіть в кв. см ( округливши її до цілого числа). Величини кутів та довжини сторін на малюнку не відповідають дійсності.
