 |
|
Порядок выполнения работы
1. По барометру определить атмосферное давление.
2. Открыть краны К1, К2, записать начальную температуру Т0.
3.Закрыть краны К1, К2, включить нагреватель. После того как водяная баня нагреется на 4-60С, отключить нагреватель и выждать момент, когда температура в бане и высота столбика в манометре перестанут изменяться,  записать показания T, h, H.
записать показания T, h, H.
4.Подобные измерения провести до температуры 800С, сняв 10-12 значений h, H. Данные записать в таблицу 3.2.

Обработка результатов эксперимента.
Рассчитать парциальное давление газа в сосуде  ,согласно уравнению (3.9.). Значение
,согласно уравнению (3.9.). Значение  , соответствующее начальной температуре опыта, взять из табл. 3.1.
, соответствующее начальной температуре опыта, взять из табл. 3.1.
Таблица 3.1.
| T0 C | ||||||||||||
| P0пмм рт. ст. | 12,79 | 13,63 | 14,53 | 15,48 | 16,48 | 17,54 | 18,65 | 19,83 | 21,07 | 23,38 | 23,76 | |
| P0п 10-2 Па | 17,0 | 18,1 | 19,3 | 20,6 | 21,9 | 23,3 | 24,8 | 26,4 | 28,0 | 29,8 | 31,4 | |
Произвести расчеты р/, р1 и гидростатического давления ргс. Данные занести в табл.3.2.
Таблица 3.2.
| № п/п | T, K | Н | h | р/ | ргс | р1 | рn |
Задание А
На основании полученных данных построить графики зависимости рn = f (Т); р1 = f (Т); р/ = f (Н).
Задание Б
Используя уравнение (3.2), рассчитать средние удельную и молярную теплоту парообразования воды в исследованном интервале температур. Для этой цели сделать следующие преобразования. В уравнении (3.2.) предположим, что υ1 <υ2, и выразим удельный объем насыщенного пара из уравнения Менделеева-Клапейрона:
 (3.11)
(3.11)
где М - молярная масса пара;
R - универсальная газовая постоянная.
После преобразования уравнения (3.2) с учетом (3.11) получим
 (3.12)
(3.12)
После интегрирования выражение для удельной теплоты парообразования примет вид
 (3.13)
(3.13)
Для расчета l построить графики
Рассчитать молярную теплоту парообразования для воды по уравнению
Контрольные вопросы
1.Написать основное уравнение кинетической теории газа.
2.Как зависит давление газа от температуры при постоянном объеме?
3.В чем отличие насыщенных паров от ненасыщенных?
4.Объяснить на основе молекулярно-кинетической теории, почему давление насыщенного пара с повышением температуры изменяется нелинейно.
5.Дать определение и указать единицы измерения удельной и молярной теплоты парообразования.
ЛАБОРАТОРНАЯ РАБОТА 1.2.4
Определение коэффициента вязкости
и диаметра молекул воздуха
Т е о р е т и ч е с к и е п о л о ж е н и я
Во всех реальных газах и жидкостях при перемещении одного слоя относительно других приходят в движение и окружающие слои. Со стороны слоя, движущегося более быстро, на слой, движущийся медленнее, действует ускоряющая сила, и наоборот. Эти силы получили название сил внутреннего трения и направлены по касательной к поверхности слоев (рис.4.1). Сила внутреннего трения определяется по закону Ньютона:

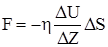 , (4.1)
, (4.1)
где -  градиент скорости, показывающий изменение скорости на единицу длины в направлении, перпендикулярном вектору скорости,
градиент скорости, показывающий изменение скорости на единицу длины в направлении, перпендикулярном вектору скорости,
ΔЅ – площадь соприкосновения слоев. 
Величина η, зависящая от природы газа и условий, в которых он находится, называется коэффициентом динамической вязкости. Коэффициент динамической вязкости η численно равен силе внутреннего трения, приходящейся на единицу площади соприкосновения слоев при градиенте скорости, равном единице.
С точки зрения молекулярно – кинетической теории в потоке газа молекулы участвуют в двух движениях: 1)тепловом со скоростью υ, равной средней арифметической скорости движения молекул при данной температуре, одинаковой у всех молекул; 2) направленном движении со скоростью ũ вместе со своим слоем. Переходя из слоя в слой в результате теплового движения, молекулы переносят с собой избыток или недостаток направленного импульса mũ по отношению к молекулам данного слоя и тем самым ускоряют или замедляют движение этого слоя.
Цель данной работы – определение коэффициента внутреннего трения воздуха и эффективного диаметра молекул воздуха (кислород и азот).
Для определения η воспользуемся законом Пуазейля о протекании газа через капиллярную трубку:

 (4.2)
(4.2)
где V – объем газа, протекшего через капилляр радиусом r и длиной l за время t;
Δp - перепад давления на концах капилляра.
Из уравнения (4.2) находим
 (4.3)
(4.3)
О п и с а н и е у с т а н о в к и
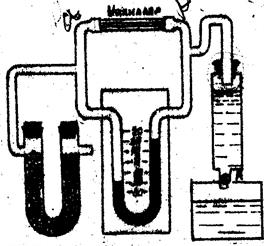 Установка для определения коэффициента динамической вязкости (4.2) состоит из капилляра, манометра, делительной воронки, мензурки и влагопоглотителя. Если открыть кран К, вода из делительной воронки начнет вытекать, давление понизится и атмосферный воздух через капилляр потечет в делительную воронку. Манометр покажет перепад давления на концах капилляра, а объем вытекшей воды будет равен объему воздуха, прошедшему через капилляр за время t. Зная радиус и длину капилляра, можно рассчитать коэффициент динамической вязкости воздуха по уравнению (4.3).
Установка для определения коэффициента динамической вязкости (4.2) состоит из капилляра, манометра, делительной воронки, мензурки и влагопоглотителя. Если открыть кран К, вода из делительной воронки начнет вытекать, давление понизится и атмосферный воздух через капилляр потечет в делительную воронку. Манометр покажет перепад давления на концах капилляра, а объем вытекшей воды будет равен объему воздуха, прошедшему через капилляр за время t. Зная радиус и длину капилляра, можно рассчитать коэффициент динамической вязкости воздуха по уравнению (4.3).
П о р я д о к в ы п о л н е н и я р а б о т ы
1. Открыть кран К, подождать, пока течение воздуха в капилляре установится, то есть уровень жидкости в манометре перестанет изменяться. При этом
 ,
,
где ρ – плотность жидкости в манометре (вода);
Δh – разность высот жидкости в коленах манометра.
2. Подставить вместо стакана под струю мензурку и, включив секундомер, измерить объем жидкости, вытекшей из делительной воронки (равный соответственно объему газа, прошедшему через капилляр) в течение 40-50 с.
3. Рассчитать коэффициент динамической вязкости по уравнению (4.3), которое с учетом (4.4) принимает вид
 . (4.5)
. (4.5)
4. Опыт повторить пять раз при разной скорости вытекания воды из делительной воронки (разных Δр), регулируя ее краном К.
5. Данные эксперимента занести в таблицу.
l = r =
| № п/п | Δh | t | V | η | d |
О б р а б о т к а р е з у л ь т а т о в э к с п е р и м е н т а
Из молекулярно – кинетической теории следует, что для идеальных газов
 , (4.6)
, (4.6)
где ρ – плотность воздуха;
- средняя арифметическая скорость молекул воздуха;
lпр - средняя длина свободного пробега молекул.
Из уравнения Менделеева – Клапейрона плотность
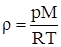 . (4.7)
. (4.7)
Средняя арифметическая скорость
 , (4.8)
, (4.8)
Средняя длина свободного пробега связана с диаметром молекулы следующим соотношением:
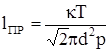 , (4.9)
, (4.9)
где р – атмосферное давление;
Т – абсолютная температура воздуха во время опыта.
Решив совместно уравнения (4.6), (4.7), (4.8), (4.9), получим
 , (4.10)
, (4.10)
где μ =29×10-3 кг/моль- средняя молярная масса воздуха;
NА – постоянная Авогадро;
R – универсальная газовая постоянная;
d – эффективный диаметр молекулы.
Подставив в уравнение (4.8) значения μ, NА, R, получим
 . (4.11)
. (4.11)
Рассчитать абсолютную и относительную погрешности для коэффициента вязкости.
Ко н т р о л ь н ы е в о п р о с ы
1. Как рассчитать давление столба жидкости высотой h?
2. Каким образом создается перепад давления на концах капилляра? Как его измерить?
3. Пояснить природу внутреннего трения в газах согласно молекулярно – кинетической теории.
4. Физический смысл коэффициента динамической вязкости и градиента скорости. Единицы их измерения.
5. Показать, как зависит коэффициент динамической вязкости газа от температуры и давления.
Л А Б О Р А Т О Р Н А Я Р А Б О Т А 1.2.5
Изучение испарения жидкости и определение
коэффициента диффузии пара
Т е о р е т и ч е с к и е п о л о ж е н и я
Если в сосуд налить жидкость, то она будет испаряться. Одновременно с испарением будет протекать и обратный процесс- конденсация пара. Если жидкость находится в закрытом сосуде, то по истечении некоторого времени, зависящего от условий, устанавливается динамическое равновесие между жидкостью и паром: число молекул, возвращающихся в жидкость за тот же промежуток времени. Пар, находящийся в динамическом равновесии с жидкостью, называется насыщенным. Давление насыщенного пара не зависит от объема и быстро растет с повышением температуры.
Допустим теперь, что жидкость находится в открытом сосуде, например, в открытом вертикальном цилиндре (см. рисунок). У поверхности жидкости в сосуде образуется слой насыщенного пара, плотность которого обозначим ρн (кг/м3). У верхнего конца цилиндра, благодаря воздушным потокам и рассеянию, плотность насыщенного пара ρ практически равна нулю.
Направим по оси цилиндра координатную ось х. Вдоль этой оси плотность насыщенного пара ρ будет равномерно убывать. Градиент плотности насыщенного пара исследуемой жидкости 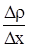 можно найти из соотношения:
можно найти из соотношения:
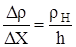 , (5.1)
, (5.1)
где h – расстояние от поверхности жидкости до края цилиндра.
При наличии градиента концентрации вдоль оси х в этом направлении протекает процесс диффузии пара, результатом которого явится непрерывный отвод от жидкости. Жидкость испаряется, а ее уровень в цилиндре понижается. Скорость испарения жидкости определяется скоростью процесса диффузии, то есть масса жидкости Δmисп, испарившейся за время Δt, равна массе пара Δmn, продиффундировавшего за этот промежуток времени вдоль оси х вверх. По закону Фика
 , (5.2)
, (5.2)
где Д – коэффициент диффузии пара данной жидкости в воздухе;
S – площадь поперечного сечения цилиндра.
В условиях данного опыта масса испарившейся жидкости может быть найдена из соотношения
 , (5.3)
, (5.3)
где ρж – плотность данной жидкости;
Δх – понижение уровня испарившейся жидкости.