Главная | Обратная связь

Глава 5. РЕАЛЬНЫЕ ГАЗЫ

На рис. 69 представлены результаты экспериментальных исследований состояний газа.

Для идеального газа изотермы в координатах являются прямыми линиями, параллельными оси , а - равнобочными гиперболами. Как следует из приведенных графиков, расхождения с экспериментами весьма значительные. Пожалуй, первыми систематическими исследованиями были работы Эндрюса по углекислому газу (1869г). Ему удалось при температуре, ниже , изотермическим сжатием получить двухфазную систему - жидкость и ее насыщенный пар.

На рис. 70 приведена изотерма Эндрюса для температуры . В цилиндре под поршнем сжимался газ по кривой «c-b». При дальнейшем сжатии, после точки «b», появилась жидкость. Еёмалое количество находилось в равновесии со своим насыщенным паром. Далее, по прямой «b-a», масса пара уменьшалась, масса жидкости возрастала, а давление оставалось постоянным. В точке «a» весь пар превращался в жидкость, после чего сжималась жидкость.

Для определения соотношения между массами жидкости и насыщенного пара в цилиндре с переменным объёмом , а так же между их объёмами и , удобно использовать диаграмму (рис. 71). На ней введены обозначения: на левом рисунке:

- величина объёма жидкости, при её полной конденсации.

- величина объёма пара, при начале конденсации.

- величина объёма в цилиндре под поршнем.

На правом рисунке:

-общая масса жидкости и пара в объёме .

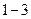- величина объёма в положении .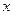

1-2 - величина объёма пара в положении .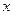

2-3 - величина объёма жидкости в положении .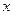

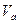Из диаграммы следует, что величина численно равна плотности насыщенного пара при этой изотерме; величина - плотности жидкости при этой изотерме. Отсюда ясно, что при изменении (точка «1» перемещается по отрезку «5- », а точка «3» по отрезку «4- ») точка «2» продолжает делить объём цилиндра на объём пара и на объём жидкости и массу вещества на массу пара («2-5») и жидкости («2-0)». Рассматривая «заштрихованные» треугольники, можно получить известное «правило рычага» .

Приведённые результаты экспериментальных исследований показывают, что при высоких давлениях свойства реального газа значительно отличаются от свойств идеального газа. Это отклонение потребовало изменение модели газ. Вместо системы невзаимодействующих материальных точек следует принять модель совокупности молекул конечных размеров, испытывающих силы притяжения между собой. Такой модели должно соответствовать и другое уравнение состояния. Новое уравнение, уравнение состояния реального газа было предложено в 1873году Ван-дер-Ваальсом.

Уравнение Ван-дер-Ваальса

Уравнение Ван-дер-Ваальса было построено из уравнения Клапейрона – Менделеева путем «поправок», учитывающие силы притяжения и конечный объём молекул. Это уравнение имеет вид:

. (5.1)

В этих же обозначениях уравнение Клапейрона – Менделеева:

.

Здесь - число молекул в объёме газа, 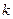- постоянная Больцмана. В более привычном виде уравнение Ван-дер-Ваальса (для моля газа) записывается соотношением:

, (5.2)

где: - величины, носящие название «постоянные Ван-дер-Ваальса», - «поправка на давление», - «поправка на объём».

Поправка на объём

Величина принимается как учетверённый объём одной молекулы (рис. 72).

 

Поскольку «недоступный» объём для центра масс налетающей молекулы при парных столкновениях равен . При расчете на одну молекулу, получим: .

Если мы обозначили мольный объём реального газа, тогда следует считать доступным объёмом для движения центров масс молекул, т.е. объёмом идеального газа .

Поправка на давление

Ван-дер-Ваальсом введены в рассмотрение слабые силы притяжения; они и уменьшают давление реального газа. На Рис.73 представлена схема, поясняющая этот эффект. Уменьшение импульса летящей к стенке молекулы определяется силами притяжения со стороны окружения. Величина этой силы пропорциональна концентрации частиц . Уменьшение потока импульса, а значит и уменьшение давления, пропорционально концентрации летящих к стенке молекул. Отсюда понятно, что , и поправка на давление определена в виде: . Давление реального газа теперь представляется соотношением . Или . Записывая уравнение Клапейрона – Менделеева в параметрах реального газа, получается уравнение Ван-дер-Ваальса

.

Уравнение Ван-дер-Ваальса как математическое соотношение

Для рассмотрения этого, приведем слагаемые к общему знаменателю и представим в виде полинома:

.

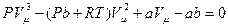Или:

.

В общем случае это уравнение третьей степени имеет три корня, причём:

1) все три корня разные действительные числа;

2) все три корня равные действительные числа;

3) один корень действительный, а два других являются комплексно-сопряженными.

Реализация этих случаев определяются величинами 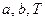. Вид кривых , при 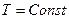, (изотермы) представлены на рис. 75.

Кроме этого, в точке , называемой критической точкой, обращаются в нуль, как первая, так и вторая производные ( ); в этой точке становятся равными все три корня уравнения.

Уравнение Ван-дер-Ваальса и свойства реального газа

При температурах выше критической температуры, область относится к газовому состоянию и достаточно точно описывает это состояние.

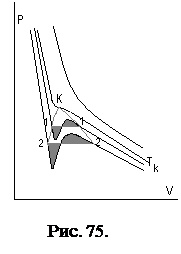
На рис. 76 выделены области, которые определены критической изотермой и кривой «2-1-К-1-2», (она носит название «спинодаль»). Особое внимание мы уделим области жидкость + насыщенный пар. Здесь проявляются качественные различия вида изотерм Ван-дер-Ваальса, и практических изотерм.

В этой области изотермы имеют вид рис. 77.

 

На рисунке представлен отрезок «a-b» практической изотермы, полученной при расширении. Во время перехода в область двухфазной системы «1-2» реализуется отрезок « ». Здесь ещё жидкость, но состояние нестабильное и система скачком переходит на прямую «1-2». Дальнейшее расширение происходит плавно по изобаре до точки «2», где жидкая фаза исчезает. При сжатиииз точки «b» по изотерме реализуется нестабильный участок « ». Это состояние пересыщенного пара. Переход в стабильное состояние (на отрезок «2-1») происходит так же скачком с образованием двухфазной системы, На рис. представлен - образный участок изотермы Ван-дер-Ваальса. Участок «c-d» этой кривой в эксперименте никогда не реализуется. Теоретически он является абсолютно неустойчивым.

Критическое состояние и его особенность

Критическое состояние реализуется на критической изотерме в одной точке. Её координаты в - пространстве обычно обозначают . Принято критическую температуру определять как температуру, выше которой путём изотермического сжатия нельзя получить двухфазную систему жидкость + насыщенный пар.

Особенность критического состояния

1). В этом состоянии свойства жидкости и её насыщенного пара одинаковы, в частности, равны плотности жидкости и пара, т.е. .

2). Изотермическая сжимаемость стремится к бесконечности, . Благодаря этому вблизи критического состояния сильно развиты флюктуации плотности.

Реализация критического состояния в эксперименте

Рассмотрим опыт по наблюдению перехода жидкости, запаянной в стеклянной ампуле, через критическое состояние. Этот опыт был предложен русским физиком Авенариусом. В физическом практикуме по курсу опыт представлен в специальной лабораторной работе (рис. 78).

В три ампулы одинакового объёма залиты разные массы одного и того же вещества, причем 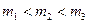. Этим ампулам соответствуют три разные диаграммы (1,2,3), но на них величина объёма ампулы одинакова. С увеличением массы диаграмма сдвигается вдоль оси . В опыте все три ампулы нагреваются одновременно, отчего в них при постоянном объёме растет давление (в основном за счет зависимости давления насыщенного пара от температуры). В первой ампуле мениск жидкости медленно опускается вниз и исчезает внизу – жидкость испарилась. В третьей ампуле мениск поднимается вверх, где и исчезает, жидкость заполняет всю ампулу. В средней ампуле, где залита критическая масса жидкости, мениск доходит лишь до середины ампулы и здесь исчезает при достижении критической температуры. Измеряя температуру исчезновение мениска в этой ампуле при нагревании и появление его при остывании, достаточно точно можно определить критическую температуру. При подходе к критической точке (особенно при медленном охлаждении), наблюдается почернение ампулы. Это явление опалесценции - рассеяние света на сильно развитых флюктуациях плотности в критическом состоянии. Ампулы обычно заполнены этиловым эфиром. Данные для этого вещества.

Критическая температура .

Критическое давление .

Отношение объёма жидкости

в ампуле, при температуре , к объёму ампулы .

Уравнение Ван-дер-Ваальса и критическое состояние

В теории Ван-дер-Ваальса критическое состояние определяется как точка в пространстве - координат, в которой все три корня уравнения совпадают. В этом случае уравнение

может быть представлено в виде: . Раскрывая это соотношение, получим:

.

Приравнивая коэффициенты при соответствующих степеней данных уравнений, придём к системе:

,

,

.

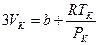Решая совместно эту систему, получим соотношения, определяющие связь постоянных Ван-дер-Ваальса с критическими параметрами.

, , . (5.3)

Достаточно точно можно измерить величины , откуда рассчитываются 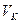и постоянные и . Следует напомнить, что здесь объём является объёмом моля.

, , .

Следует отметить, что при экспериментальном определении всех трёх критических параметров соотношение выполняется лишь приближенно. Обычно несколько больше.

Приведем вид уравнения Ван-дер-Ваальса для произвольного числа молей :

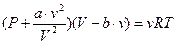. (5.4)

Приведенное уравнение Ван-дер-Ваальса

Если ввести безразмерные параметры состояния , и учесть, что 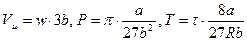- то получим уравнение:

. (5.5)

Это и есть приведенное уравнение Ван-дер-Ваальса.

Внутренняя энергия газа Ван-дер-Ваальса

Поскольку «поправку на давление» следует определять как существование «внутреннего» давления , которое порождено потенциальными силами межмолекулярными притяжения, то можно ввести потенциальную энергию системы частиц. По определению . Величина элементарной работы сил притяжения для моля газа будет равна: . Откуда . Потенциальная энергия, в состоянии с заданным , определится соотношением:

. (5.6)

Сохраняя соотношение кинетической энергии для реального газа таким же, как и для идеального газа , определим внутреннюю энергию газа Ван-дер-Ваальса в виде:

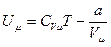. (5.7)

Опыты по изучению зависимости внутренней энергии газа от объёма

Первые такие опыты были отмечены в работах Гей-Люссака. Более систематическими опытами считаются опыты Джоуля (1845 г.). В них были проведены исследования изменения температуры газа при его адиабатическом расширении в «пустоту». Схема опытов представлена на рис. 79. В теплоизолирующую оболочку 4 помещались баллоны 1 и 2. Они соединялись трубкой с краном 3 . Газом заполнялся баллон 1, а второй откачивался. Измерялась температура газа . Далее, кран 3 открывался, и давление в баллонах выравнивалось. Несмотря на то, что температуры измерялись с весьма малой погрешностью 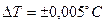, изменение температуры обнаружить не удалось. В опытах использовались два одинаковых медных сосуда с объёмом 2,36л. Первоначальное давление газа составляло 20атм. Для процесса, который осуществляется газом в этом опыте, выполняется условие , или . Такое заключение следует из первого закона термодинамики , процесс адиабатический , расширение в пустоту . Откуда следует принять, что энергия исследуемого газа не зависит от объёма, а зависит только от температуры. Кроме этого, состояния газа, которые реализовались в опытах, подчинялись закону Бойля – Мариотта. Значит, эти опыты и их результаты относятся к идеальному газу. Утверждение, что энергия идеального газа не зависит от объёма, а зависит только от температуры, получило название закона Джоуля.

Эффект Джоуля – Томсона

Критический анализ проведенных опытов Джоуля, послужили появлению новых опытов для исследования зависимости внутренней энергии газов от объёма. Дело в том, что большая теплоемкость баллонов по сравнению с теплоемкостью газа, находящегося в хорошем тепловом контакте с ними, практически, сводила к нулю изменение температуры газа в опытах. В новых опытах, проведенных Джоулем и Томсоном (лорд Кельвин) в 1852г, был использован стационарный поток газа с «расширением» (рис. 80).

Через теплоизолированную цилиндрическую ячейку, разделенную на две части пористой перегородкой, пропускается исследуемый газ. Проток газа с нужными параметрами определяется внешними системами. Поскольку ячейка цилиндрическая, удельный объем , и давление являются постоянными величинами по пространству. При протекании газа через пористую перегородку давление уменьшается, а удельный объем возрастает, (газ расширяется), Рис.80. В установившемся режиме течения измеряются температуры и . В этих опытах, в качестве измерительной ячейки был использован отрезок бамбуковой трубки, обернутый слоем шерсти. Пористой перегородкой служил ватный помпон. Температура измерялась термометрами. В проведенных исследованиях было обнаружено, что для комнатной температуры при изменении давления от 2атм до 1атм температура газа изменялась:

Воздух .

Углекислый газ .

Водород .

В противоположность выводам из результатов опытов Джоуля, следовало принять, что внутренняя энергия реального газа зависит от его объёма. Хотя эта зависимость не была установлена по полученным результатам, было установлено не известное ранее явление – явление изменения температуры газа при «дросселировании». Это явление получило название эффекта Джоуля – Томсона. Сначала эффект казался весьма сложным в объяснении, поскольку изменение температуры зависело не только от рода газа но и от параметров состояния . Для количественной оценки вводится дифференциальный коэффициент эффекта . Если - эффект считается положительным (при этом , поскольку всегда ). При нулевом коэффициенте температура не меняется – нулевой эффект, а если 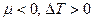эффект Джоуля – Томсона считается отрицательным.

В дальнейшем эффект был объяснен, в рамках молекулярно-кинетических представлений и термодинамики. В нашем курсе мы познакомимся лишь с элементами этих объяснений. Во-первых, покажем, что при стационарном протоке газа через пористую перегородку (дроссель), сохраняется величина , где - внутренняя энергия газа. Для этого смоделируем поток газа, используя движение двух «мысленных» поршней (рис. 81). Поршень 1 при давлении «проталкивает» через дроссель объём . Поршень 2 при этом перемещается, и газ, при давлении , занимает объём . Поршень 1, как внешнее для газа тело, совершает работу 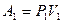, поршень 2, при этом, совершает работу . Общая работа внешних тел . Течение газа считается адиабатическим, так что изменение внутренней энергии равно работе внешних сил . Откуда:

. (5.8)

Функция носит в термодинамике название энтальпия.

Изменение внутренней энергии при дросселировании может быть определено по работе сил давления . Для идеального газа эта работа, (отнесенная к молю газа) равна нулю. Из уравнения Клапейрона – Менделеева она равна , но . Действительно, поскольку для идеального газа 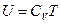, то, из уравнения , следует соотношение: 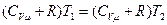. Откуда и получается, что . Проведенное рассмотрение показывает, что для идеального газа при дросселировании работа газа равна нулю, внутренняя энергия не меняется, не изменяется и температура газа. В реальном газе, где между частицами действуют силы отталкивания и силы притяжения, изменение температуры газа при дросселировании свидетельствует о зависимости внутренней энергии от объёма.

Сделаем оценку эффекта Джоуля – Томсона для газа Ван-дер-Ваальса.

При дросселировании .

Внутренняя энергия .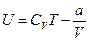

Уравнение состояния .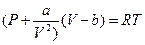

Из уравнения состояния, с определенным приближением, определим .

.

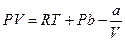Откуда, с учетом соотношения для внутренней энергии, получим:

.

Или: .

Сделаем еще одно приближение, считая, что и . После этого придём к соотношению:

. (5.9)

Откуда, коэффициент Джоуля – Томсона принимает вид:

. (5.10)

Поскольку при дросселировании всегда , знак будет определяться числителем соотношения. Нулевой эффект соответствует температуре , она носит название температуры инверсии. При более низкой температуре превалируют силы отталкивания – газ охлаждается; при высокой температуре – он нагревается.

Эффект Джоуля – Томсона имеет широкое техническое применение в установках для охлаждения газов, включая их сжижение. Примером такой установки может служить машина Линде.

Задание. Рассмотреть по учебникам схему машины Линде, обратив особое внимание на параметры газа при её работе.