 |
|
Глава 6. ЭЛЕМЕНТЫ ТЕОРЕТИЧЕСКОЙ ТЕРМОДИНАМИКИ
Приведем некоторые важные определения.
Обратимые процессы
Пусть термодинамическая система переходит из состояния «1» в состояние «2». Процесс перехода называется обратимым, если обратный переход из «2» в «1» по тем же состояниям можно осуществить без каких либо изменений в состояниях окружающих систему тел.
Необратимые процессы
Процесс перехода называется необратимым, если обратный переход из «2» в «1» по тем же состояниям нельзя осуществить без каких либо изменений в состояниях окружающих систему тел.
Квазистатический процесс является обратимым, поскольку в квазистатическом процессе параметры состояния выделенной системы в каждый момент времени полностью определяются внешними параметрами.
При обратимом процессе система проходит все время равновесные состояния, и такой процесс называют равновесным процессом. При необратимом процессе система проходит через неравновесные состояния (хотя бы частично), и процесс называют неравновесным процессом.
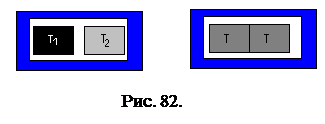 Примеры необратимых процессов. Пусть два тела с разными температурами
Примеры необратимых процессов. Пусть два тела с разными температурами 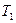 и
и  , причем
, причем  , находятся в теплоизолирующей оболочке (рис. 82).
, находятся в теплоизолирующей оболочке (рис. 82).
При осуществлении теплового контакта между телами, реализуется процесс теплопередачи. В результате этого, тела принимают одинаковую температуру  , причем
, причем 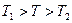 . Этот процесс является неравновесным, поскольку существовала неоднородность температуры по пространству. Процесс является и необратимым, поскольку для уменьшения температуры второго теля с одновременным увеличением её у первого тела необходимы внешние тела (например, холодильник).
. Этот процесс является неравновесным, поскольку существовала неоднородность температуры по пространству. Процесс является и необратимым, поскольку для уменьшения температуры второго теля с одновременным увеличением её у первого тела необходимы внешние тела (например, холодильник).
 Вторым примером может служить процесс расширения газа в пустоту (рис. 83). Сначала в сосуде 1 давление газа
Вторым примером может служить процесс расширения газа в пустоту (рис. 83). Сначала в сосуде 1 давление газа  , а второй откачен. После открытия соединительного крана, газ частично перетекает во второй и давление выравнивается. Процесс перетекания газа является неравновесным и необратимым. Можно ли вернуть систему в начальное состояние? Наверное, возможно, но для этого газ в сосуде 2 необходимо сжимать, совершая внешнюю работу, и отбирать тепло, поскольку при сжатии газ будет нагреваться. Откуда следует, что для обратного процесса нужны «работающие» внешние тела. В дальнейшем будем рассматривать равновесные, обратимые процессы. Рассмотрение неравновесных процессов будем проведено позже.
, а второй откачен. После открытия соединительного крана, газ частично перетекает во второй и давление выравнивается. Процесс перетекания газа является неравновесным и необратимым. Можно ли вернуть систему в начальное состояние? Наверное, возможно, но для этого газ в сосуде 2 необходимо сжимать, совершая внешнюю работу, и отбирать тепло, поскольку при сжатии газ будет нагреваться. Откуда следует, что для обратного процесса нужны «работающие» внешние тела. В дальнейшем будем рассматривать равновесные, обратимые процессы. Рассмотрение неравновесных процессов будем проведено позже.
В теоретической термодинамике состояние системы определяется точкой в пространстве 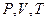 состояний. При совершении системой равновесного процесса, состояние ее меняется, и этот процесс можно изображать в пространстве
состояний. При совершении системой равновесного процесса, состояние ее меняется, и этот процесс можно изображать в пространстве 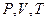 состояний непрерывной кривой. Фактор времени при этом не отражается. Считается, что параметры состояния в каждом участке термодинамической системы одинаковы и меняются одновременно. Было бы красиво и наглядно, если бы характер процесса изображали кривой на поверхности
состояний непрерывной кривой. Фактор времени при этом не отражается. Считается, что параметры состояния в каждом участке термодинамической системы одинаковы и меняются одновременно. Было бы красиво и наглядно, если бы характер процесса изображали кривой на поверхности 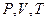 , заданной термическим уравнением состояния. Это громоздко, а иногда и трудно, поэтому используют «плоские» кривые
, заданной термическим уравнением состояния. Это громоздко, а иногда и трудно, поэтому используют «плоские» кривые 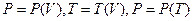 .
.
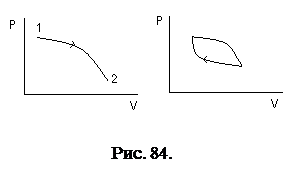 Циклические процессы
Циклические процессы
Из различных процессов, особо выделяют циклические процессы. Кривые состояний являются замкнутыми кривыми. Иногда, при этом подразумевается, что система «движется» по этой кривой и состояния ее периодически меняются, (отсюда и название циклические).
На первом рисунке система переходит из состояния 1 в состояние 2 на втором - система совершает циклический процесс.
Особенности циклического процесса
 Пусть система из состояния «А», совершив циклический процесс, вновь вернется в состояние «А» (рис. 85).
Пусть система из состояния «А», совершив циклический процесс, вновь вернется в состояние «А» (рис. 85).
В таком процессе:
1). За весь процесс, изменение внутренней энергии равно нулю, поскольку внутренняя энергия определяется состоянием, а система вернулась в исходное состояние:
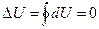 . (6.1)
. (6.1)
2). Работа системы за один цикл  равна теплоте, отданной (принятой) системой
равна теплоте, отданной (принятой) системой 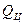 :
:
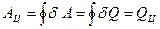 . (6.2)
. (6.2)
Эта особенность следует из первого закона термодинамики: 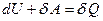 . Интегрируя изменение за цикл
. Интегрируя изменение за цикл  , и учитываем, что
, и учитываем, что 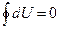 , получим:
, получим: 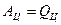 . В частности, как это показано на второй диаграмме (рис. 85), работа и теплота за цикл равны нулю.
. В частности, как это показано на второй диаграмме (рис. 85), работа и теплота за цикл равны нулю.
Тепловые машины, теоремы Карно
Началом создания теоретической термодинамики, пожалуй, можно считать опубликованную в 1824 г. Саади Карно работу «Размышление о движущей силе огня и о машинах, способных развивать эти силы». К тепловым машинам следует отнести тепловые двигатели, производящие работу за счет потребления теплоты от нагревателя, и холодильные машины, отбирающих теплоту от заданной системы, за счет работы внешних систем. Схематическое представ 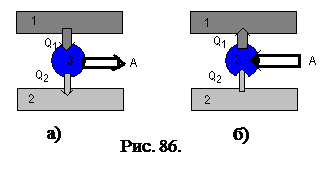 ление этих машин приведено на рис. 86.
ление этих машин приведено на рис. 86.
Схема а) – схема теплового двигателя. Здесь: 1 – нагреватель, отдающий рабочему телу 3 теплоту  . 2 – холодильник, отбирающий от рабочего тела теплоту
. 2 – холодильник, отбирающий от рабочего тела теплоту  . Вся система 1,2,3 совершает работу
. Вся система 1,2,3 совершает работу 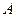 , «отдавая» ее внешним телам.
, «отдавая» ее внешним телам.
Схема б) – схема холодильной машины. Здесь: 1 – теплоприемник, отбирающий от рабочего тела теплоту  . 2 – охлаждаемое тело, от которого отбирается теплота
. 2 – охлаждаемое тело, от которого отбирается теплота  рабочим телом 3. Для осуществления этих процессов, рабочее тело «потребляет» работу
рабочим телом 3. Для осуществления этих процессов, рабочее тело «потребляет» работу 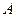 внешних тел.
внешних тел.
Тепловые двигатели и их коэффициент полезного действия
Для характеристики двигателя вводят его коэффициент полезного действия
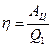 . (6.3)
. (6.3)
Рабочее тело совершает работу против внешних сил и 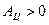 .
.
Двигатель совершает циклические процессы, но удобнее говорить лишь об одном цикле, и, чтобы не загромождать соотношения, будем опускать написание индекса «Ц». Поскольку 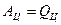 , а теплота за цикл равна алгебраической сумме теплот (
, а теплота за цикл равна алгебраической сумме теплот ( 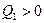 и
и 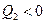 ), т.е.
), т.е. 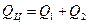 , то, с использованием модулей величин, можно записать:
, то, с использованием модулей величин, можно записать:
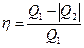 . (6.4)
. (6.4)
Как и всякий коэффициент полезного действия машины 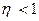 .
.
Холодильная машина
Если холодильная машина предназначена для охлаждения какого-то тела, то ее эффективность характеризуется холодильным коэффициентом  . По определению, он равен:
. По определению, он равен: 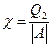 . Для этой машины
. Для этой машины  >0 – теплота «поступает» к рабочему телу;
>0 – теплота «поступает» к рабочему телу;  <0 - теплота «отбирается» от рабочего тела; работа рабочего тела
<0 - теплота «отбирается» от рабочего тела; работа рабочего тела 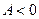 . Поскольку
. Поскольку 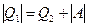 , для холодильного коэффициента получим соотношение:
, для холодильного коэффициента получим соотношение:
 . (6.5)
. (6.5)
Холодильный коэффициент 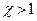 . Следует отметить, что холодильный коэффициент не является энергетическим коэффициентом полезного действия холодильной машины. Если вводить КПД, как отношение «полезной энергии» к «затраченной» для ее получения, то он должен определяться соотношением
. Следует отметить, что холодильный коэффициент не является энергетическим коэффициентом полезного действия холодильной машины. Если вводить КПД, как отношение «полезной энергии» к «затраченной» для ее получения, то он должен определяться соотношением
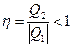 .
.
Если холодильную машину использовать как «нагреватель», то эффективность её определяют коэффициентом
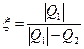 .
.  . (6.6)
. (6.6)
Иногда удобно использовать терминологию, согласно которой тепловые двигатели, это тепловые машины, работающие по прямому циклу. Холодильные – тепловые машины, работающие по обратному циклу (рис. 87). 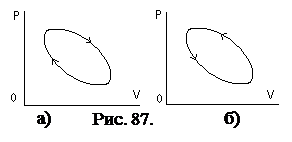 На схеме а) - прямой цикл, на б) – обратный цикл.
На схеме а) - прямой цикл, на б) – обратный цикл.
Важное утверждениедля циклических процессов,являющееся обобщением опыта, приведем формулировку принципа В.Томсона. «Невозможно осуществить циклический процесс, единственным результатом которого было бы превращением в работу тепла, отнятого у какого-нибудь тела, без того, что бы не произошли какие-либо изменения в окружающих телах».
Цикл Карно
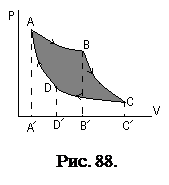 Цикл Карно построен из двух изотерм и двух адиабат (рис. 88). Выберем в качестве рабочего тела идеальный газ.
Цикл Карно построен из двух изотерм и двух адиабат (рис. 88). Выберем в качестве рабочего тела идеальный газ.  - изотерма при температуре
- изотерма при температуре 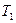 . В этом процесс от термостата с температурой
. В этом процесс от термостата с температурой 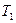 рабочее тело получает теплоту
рабочее тело получает теплоту 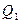 , и за счет нее совершает работу
, и за счет нее совершает работу 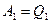 . Поскольку расширение газа происходит от объёма
. Поскольку расширение газа происходит от объёма 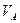 до объёма
до объёма  , эта работа (для моля газа) равна:
, эта работа (для моля газа) равна:
 .
.
Далее, при адиабатическом процессе  продолжается расширение газа с понижением температуры до
продолжается расширение газа с понижением температуры до 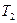 . При этом объём изменяется от
. При этом объём изменяется от  до
до  , причем
, причем
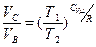 .
.
В этом процессе: 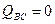 , работа равна убыли внутренней энергии
, работа равна убыли внутренней энергии
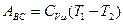 .
.
В изотермическом процессе 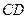 происходит сжатие газа от объёма
происходит сжатие газа от объёма  до объёма
до объёма 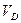 . При этом совершается отрицательная работа
. При этом совершается отрицательная работа 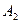 .
.
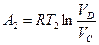 .
.
Цикл завершается адиабатой сжатия 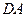 до температуры
до температуры 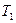 . При этом объём изменяется от
. При этом объём изменяется от 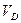 до
до 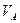 , причем
, причем
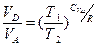 .
.
Работа 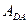 будет отрицательной и равной
будет отрицательной и равной 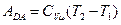 . Коэффициент полезного действия цикла, по определению, равен:
. Коэффициент полезного действия цикла, по определению, равен:
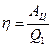 .
.
Откуда для цикла Карно:  .
.
Поскольку из уравнений адиабат следует, что  , то
, то  . После сокращений, коэффициент полезного действия идеального цикла Карно приобретает вид:
. После сокращений, коэффициент полезного действия идеального цикла Карно приобретает вид:
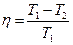 . (6.7)
. (6.7)
Теоремы Карно
Первая теорема. Коэффициент полезного действия идеального цикла Карно не зависит от рабочего вещества и предельных адиабат, а зависит только от температур теплоотдатчика и теплоприемника.
Вторая теорема. Коэффициент полезного действия необратимого цикла Карно меньше коэффициента полезного действия идеального цикла. Детальное рассмотрение этих теорем Вы будете проводить в курсе теоретической физики, а сейчас рассмотрим вторую теорему Карно для частного случая необратимости цикла.
Будем считать, что в необратимом цикле теплоотдача происходит при «разрыве» температур. Для обратимого цикла: 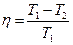 . Для необратимого цикла:
. Для необратимого цикла:
 , где
, где 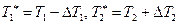 . Откуда
. Откуда 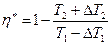 . Поскольку
. Поскольку 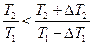 , то
, то 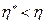 , т.е. коэффициент полезного действия необратимого цикла Карно меньше коэффициента полезного действия идеального цикла.
, т.е. коэффициент полезного действия необратимого цикла Карно меньше коэффициента полезного действия идеального цикла.
Теорема Клаузиуса о приведенной теплоте цикла. Энтропия
Для обратимого цикла Карно справедливо соотношение:
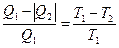 .
.
Если перейти к алгебраической форме записи, то данное соотношение можно представить в виде:
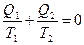 . (6.8)
. (6.8)
Величина  получила название приведенной теплоты. Само же соотношение читается как: «сумма приведенных теплот идеального цикла Карно равна нулю». Исходя из этого утверждения, Клаузиусом доказана теорема о приведенной теплоте произвольного цикла, в котором теплоотдатчик передает теплоту рабочему телу при разных температурах; разные температуры и у теплоприемника. Эта теорема утверждает, что и для произвольного обратимого цикла сумма приведенных теплот равна нулю. Покажем это, для чего разобьём произвольный цикл на элементарные циклы Карно (рис. 89). Разбиение проведено так, что сумма площадей элементарных циклов равна площади исходного цикла. Для каждого
получила название приведенной теплоты. Само же соотношение читается как: «сумма приведенных теплот идеального цикла Карно равна нулю». Исходя из этого утверждения, Клаузиусом доказана теорема о приведенной теплоте произвольного цикла, в котором теплоотдатчик передает теплоту рабочему телу при разных температурах; разные температуры и у теплоприемника. Эта теорема утверждает, что и для произвольного обратимого цикла сумма приведенных теплот равна нулю. Покажем это, для чего разобьём произвольный цикл на элементарные циклы Карно (рис. 89). Разбиение проведено так, что сумма площадей элементарных циклов равна площади исходного цикла. Для каждого 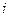 -го элементарного цикла, как цикла Карно, можно записать соотношение:
-го элементарного цикла, как цикла Карно, можно записать соотношение:
 .
.
В соответствии с рис. 89, величина 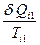 является приведенной теплотой при изотермическом процессе теплоотдачи в
является приведенной теплотой при изотермическом процессе теплоотдачи в 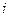 - ом элементарном цикле Величина
- ом элементарном цикле Величина 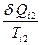 является приведенной теплотой при изотермическом процессе передачи тепла
является приведенной теплотой при изотермическом процессе передачи тепла 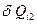 «холодильнику» в этом
«холодильнику» в этом 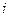 -ом элементарном цикле. При разбиении исходного цикла на
-ом элементарном цикле. При разбиении исходного цикла на 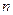 элементарных циклов можно записать
элементарных циклов можно записать 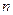 таких соотношений. Из этой системы уравнений получим уравнение
таких соотношений. Из этой системы уравнений получим уравнение
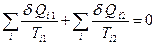 , (6.9)
, (6.9)
которое и утверждает, что и для произвольного обратимого цикла сумма приведенных теплот равна нулю. Так как сумму, при предельном разбиении, можно заменить интегралом, получим:
 .
.
Отсюда следует два важных соотношения:
 . (6.10)
. (6.10)
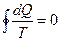 . (6.11)
. (6.11)
Энтропия. Свойства энтропии
Соотношения (6.10), (6.11) показывают, что для равновесного состояния термодинамической системы можно ввести функцию состояния  . Её бесконечно малое изменение определяется соотношением:
. Её бесконечно малое изменение определяется соотношением:
 . (6.12)
. (6.12)
По свойствам функции состояния, её изменение, при равновесных процессах, не зависит от вида процесса, а зависит лишь от начального и конечного состояний.
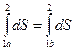 .
.
По свойствам функции состояния, 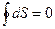 , справедливо утверждение: «изменение энтропии термодинамической системы в равновесном цикле равно нулю».
, справедливо утверждение: «изменение энтропии термодинамической системы в равновесном цикле равно нулю».
Неравновесные процесс и изменение энтропии
А). Сумма приведенных теплот в необратимых циклах. Как было отмечено, при рассмотрении необратимого цикла Карно, его коэффициент полезного действия  меньше коэффициента полезного действия обратимого цикла
меньше коэффициента полезного действия обратимого цикла 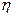 , т.е.
, т.е. 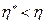 . Откуда следует соотношение
. Откуда следует соотношение
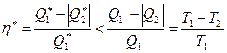 .
.
Из данного неравенства приходим к следующему неравенству  . Переходя к алгебраической форме записи, получим неравенство для суммы приведённых теплот неравновесного цикла Карно:
. Переходя к алгебраической форме записи, получим неравенство для суммы приведённых теплот неравновесного цикла Карно:
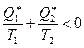 . (6.13)
. (6.13)
Это неравенство носит название неравенства Клаузиуса для приведенных теплот необратимого цикла Карно. Следует особо отметить, что в этом соотношении температуры соответствуют температурам теплоотдатчика и теплоприемника, а не температурам термодинамической системы. Если вновь использовать «разбиение» произвольного неравновесного цикла на элементарные неравновесные циклы Карно, то приходим к интегральному неравенству Клаузиуса:
 . (6.14)
. (6.14)
Более глубокие рассмотрения показывают, что при сравнении элементарных неравновесных и равновесных процессов, получающих теплоту от одного и того же теплоотдатчика, всегда реализуется неравенство  . Откуда еще одно неравенство.
. Откуда еще одно неравенство.
 . (6.15)
. (6.15)
Так как энтропия является функцией состояния, то, при переходе системы из равновесного состояния 1 в равновесное состояние 2 , будем иметь:
Для равновесного процесса
 . (6.16)
. (6.16)
Для неравновесного процесса
 . (6.17)
. (6.17)
Оставим, пока сравнение равновесных и неравновесных процессов, и рассмотрим расчеты изменения энтропии в идеальных газах при изопроцессах.
Изменения энтропии в идеальных газах при равновесных изопроцессах
Прежде чем перейти непосредственно к расчетам, получим важное уравнение термодинамики. Уравнение первого закона термодинамики имеет вид:
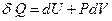 .
.
Вводя величину энтропии соотношением  , получим уравнение:
, получим уравнение:
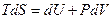 . (6.18)
. (6.18)
Это уравнение носит название основного уравнением равновесной термодинамики.
Энтропия идеального газа
Из уравнений 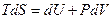 ,
,  ,
, 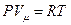 следует дифференциальное соотношение:
следует дифференциальное соотношение:
 . (6.19)
. (6.19)
После интегрирования будем иметь искомое соотношение для энтропии идеального газа:
 . (6.20)
. (6.20)
Замечание. Приведенное соотношение для энтропии определяет её зависимость от температуры и объёма 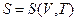 . Используя термическое уравнение, можно получить
. Используя термическое уравнение, можно получить 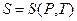
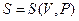 . При всех независимых переменных, энтропия определяется с точностью до постоянной величины. Определим изменение энтропии в равновесных изопроцессах.
. При всех независимых переменных, энтропия определяется с точностью до постоянной величины. Определим изменение энтропии в равновесных изопроцессах.
1). Адиабатический процесс
По определению, при адиабатическом процессе система не обменивается теплотой с окружающей средой, т.е. 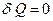 . Откуда
. Откуда 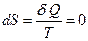 и
и
 . (6.21)
. (6.21)
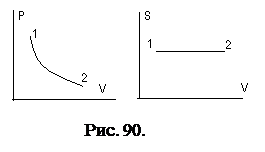 В адиабатическом процессе энтропия системы остается постоянной величиной.
В адиабатическом процессе энтропия системы остается постоянной величиной.
2). Изохорический процесс
В этом процессе  , а изменяются
, а изменяются 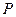 и
и 
 . Для их изменения система получает или отдает теплоту
. Для их изменения система получает или отдает теплоту 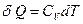 . Откуда
. Откуда  . После интегрирования, получим:
. После интегрирования, получим:
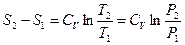 . (6.22)
. (6.22)
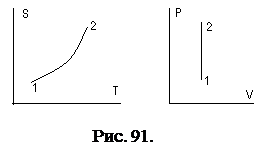
Диаграммы изменения переменных представлены на рис. 91.
3). Изобарический процесс
|
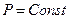 , а изменяются
, а изменяются  и
и 
 . Для их изменения система получает или отдает теплоту
. Для их изменения система получает или отдает теплоту 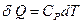 . Откуда
. Откуда 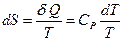 . После интегрирования, получим:
. После интегрирования, получим:
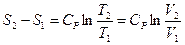 . (6.23)
. (6.23)
Диаграммы изменения переменных представлены на рис. 91.
4). Изотермический процесс
В этом процессе 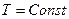 , а изменяются
, а изменяются  и
и 
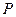 . Для расчета изменения энтропии можно использовать соотношение для энтропии, полученное ранее.
. Для расчета изменения энтропии можно использовать соотношение для энтропии, полученное ранее.
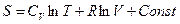 .
.
Записав это соотношение для состояний 1и 2, и проведя вычитание, получим:
 . (6.24)
. (6.24)
Это соотношение верно для одного моля газа, в предыдущих рассмотренных случаях это замечание снимается. Там 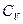 и
и  могут быть любыми. Диаграммы этого процесса представлены на рис. 92.
могут быть любыми. Диаграммы этого процесса представлены на рис. 92. 
Замечание
Целесообразно отметить два изотермических процессов, которые будем рассматривать в дальнейшем. Они относятся к фазовым переходам.
1). Переход «жидкость – пар» при температуре кипения. Для превращения моля жидкости в пар при температуре кипения необходима теплота 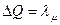 . Откуда, изменение энтропии в этом процессе равно:
. Откуда, изменение энтропии в этом процессе равно:
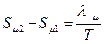 . (6.25)
. (6.25)
2). Процесс плавления – переход «кристалл – жидкость» при температуре плавления. В этом процессе кристаллом поглощается теплота плавления 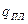 (для моля). Откуда, изменение энтропии в этом процессе равно:
(для моля). Откуда, изменение энтропии в этом процессе равно:
 . (6.26)
. (6.26)
Изменение энтропии при неравновесных процессах в изолированной системе. Пусть система является замкнутой системой. Если эта система, в исходном состоянии, находится в неравновесном состоянии, то с ней будет протекать неравновесный процесс, приводящий систему к равновесному состоянию. Такой процесс всегда сопровождается возрастанием энтропии  Докажем это утверждение на приведенных ранее неравновесных процессах.
Докажем это утверждение на приведенных ранее неравновесных процессах.
 1. Пусть два тела с разными температурами
1. Пусть два тела с разными температурами 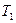 и
и 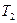 , причем
, причем 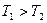 , находятся в теплоизолирующей оболочке (рис. 82). При осуществлении теплового контакта между телами, реализуется процесс теплопередачи, в результате тела принимают одинаковую температуру
, находятся в теплоизолирующей оболочке (рис. 82). При осуществлении теплового контакта между телами, реализуется процесс теплопередачи, в результате тела принимают одинаковую температуру  , причем
, причем 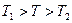 . При протекании процесса первое тело отдает теплоту
. При протекании процесса первое тело отдает теплоту  , а второе – принимает
, а второе – принимает  . Поскольку система замкнутая, в каждом элементе
. Поскольку система замкнутая, в каждом элементе 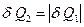 , и
, и 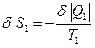 , а
, а  . Изменение энтропии системы равно сумме изменений энтропии отдельных частей системы. Откуда:
. Изменение энтропии системы равно сумме изменений энтропии отдельных частей системы. Откуда:
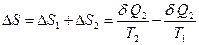 .
.
Приведя правую часть к общему знаменателю, получим:
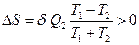 .
.
 2. Вторым примером может служить процесс расширения газа в пустоту (рис. 83). Сначала в сосуде 1 давление газа
2. Вторым примером может служить процесс расширения газа в пустоту (рис. 83). Сначала в сосуде 1 давление газа  , а второй откачен. После открытия соединительного крана, газ частично перетекает во второй и давление выравнивается. Процесс перетекания газа является неравновесным и необратимым. Поскольку мы рассматриваем процесс в идеальном газе, то, при расширении, внутренняя энергия газа не изменяется. Не изменится и температура по окончанию процесса в этой изолированной системе. По условию задачи: исходное состояние системы
, а второй откачен. После открытия соединительного крана, газ частично перетекает во второй и давление выравнивается. Процесс перетекания газа является неравновесным и необратимым. Поскольку мы рассматриваем процесс в идеальном газе, то, при расширении, внутренняя энергия газа не изменяется. Не изменится и температура по окончанию процесса в этой изолированной системе. По условию задачи: исходное состояние системы 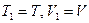 . Конечное состояние системы
. Конечное состояние системы 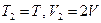 . Величина энтропии в идеальном газе определена соотношением
. Величина энтропии в идеальном газе определена соотношением
 .
.
Откуда изменение энтропии 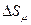 , отнесенное к молю газа, будет равно:
, отнесенное к молю газа, будет равно:
 .
.
Для нашей задачи 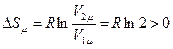 , что доказывает возрастание энтропии в этом процессе. По этому примеру можно сделать важное замечание.
, что доказывает возрастание энтропии в этом процессе. По этому примеру можно сделать важное замечание.
Замечание
Мы рассматривали изменение энтропии в этом неравновесном процессе как разность энтропий в двух состояниях. Оба состояния, начальное и конечное, определены как равновесные состояния. С другой стороны, этот неравновесный процесс в изолированной системе, можно «заменить» эквивалентным  равновесным процессом, но протекающим при внешнем воздействии. Такой «эквивалентный» процесс будет изотермическим процессом расширения газа из состояния 1 в состояние 2 при совершении работы за счет поглощения теплоты
равновесным процессом, но протекающим при внешнем воздействии. Такой «эквивалентный» процесс будет изотермическим процессом расширения газа из состояния 1 в состояние 2 при совершении работы за счет поглощения теплоты 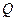 извне. Схема такого процесса представлена на рис. 93.
извне. Схема такого процесса представлена на рис. 93.
В этом равновесном процессе изменение энтропии определим как:
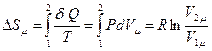 .
.
Второй закон термодинамики
Прежде чем перейти к формулировке второго закона термодинамики, приведем интересную историческую справку. Она касается существования вечного двигателя. «Вечные двигатели» разделяют на два рода. Двигатели первого рода – механические устройства, которые «должны работать» периодически и бесконечно долго без внешних воздействий. Практическая деятельность людей показывает невозможность построения таких систем. Французская академия наук в 1755 г. была вынуждена запретить принимать к рассмотрению проекты вечных двигателей «раз и навсегда». В качестве шутки отметим, что поиски обоснования невозможности вечного двигателя первого рода, привели к открытию закона сохранения энергии. Вечные двигатели второго рода, по своей сущности, более изощренные - они не противоречат закону сохранения энергии. Так тепловая машина, работающая по замкнутому циклу, «должна являться вечным двигателем», который принимает теплоту от какого-нибудь тела и полностью превращает ее в работу. Предполагали, что этим телом может служить океан с огромным запасом внутренней энергии, и тогда время работы двигателя, практически, неограниченно. Такой процесс не запрещается первым законом термодинамики. В этом плане формулировкой второго закона термодинамики может служить утверждение: «невозможно осуществление вечного двигателя второго рода».
Отдавая дань истории термодинамики, приведем ряд формулировок второго закона термодинамики.
Формулировка Карно. «Коэффициент полезного действия идеальной тепловой машины, работающему по циклу Карно, определяется только температурами теплоотдатчика и теплоприемника».
Формулировка Кельвина. «Невозможно построить тепловую машину, которая превращала бы в работу теплоту наиболее холодного из имеющихся в системе тел».
Формулировка Клаузиуса. «Теплота не может сама собой переходить от менее нагретого тела к более нагретому телу».
Формулировка Планка. «Невозможен такой периодический процесс, единственным результатом которого было бы превращение теплоты в работу».
Современные формулировки второго закона термодинамики могут быть представлены утверждением: В равновесном состоянии для термодинамической системы существует аддитивная функция состояния, называемая энтропией. В замкнутых системах равновесные процессы могут протекать так, чтобы энтропия системы оставалась постоянной величиной 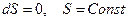 . Это относится и к адиабатическим равновесным процессам. В замкнутых системах, (или только в адиабатно изолированных), неравновесные процессы могут протекать так, чтобы энтропия системы только возрастала
. Это относится и к адиабатическим равновесным процессам. В замкнутых системах, (или только в адиабатно изолированных), неравновесные процессы могут протекать так, чтобы энтропия системы только возрастала  .
.
Весьма интересная формулировка второго закона термодинамики следует из работ Л. Больцмана, который заложил основы «механической теории теплоты». Здесь обоснованы утверждения, что равновесное состояние является наиболее вероятным состоянием. Неравновесные состояния являются менее вероятными. В замкнутых системах естественные неравновесные процессы протекают в направлении перехода системы к равновесному состоянию.
Формулировка Больцмана: «Все процессы в природе протекают в направлении, приводящем к увеличению вероятности состояния. Энтропия пропорциональна термодинамической вероятности 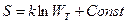 ».
».
Под термодинамической вероятностью понимают число микросостояний, которым может осуществиться данное макросостояние. По Больцману, термодинамическая вероятность (при распределении частиц по ячейкам) определяется соотношением
 , (6.27)
, (6.27)
где 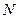 - число частиц в системе,
- число частиц в системе, 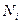 - число частиц в
- число частиц в 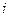 - ой ячейке.
- ой ячейке.
В качестве примера рассмотрим распределения частиц по объёму. Разобьём мысленно объём на 2 одинаковых участка и определим распределение 4-х частиц по этим ячейкам.
1). Распределение 0-4. 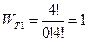 .
.
2). Распределение 1-3. 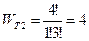 .
.
3). Распределение 2-2. 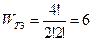 .
.
Однородное распределение частиц по пространству – наиболее вероятное (равновесное) состояние. Состояния 1 и 2 неравновесные состояния.
При переходе системы из состояния 1 в состояние 3 (естественный процесс) сопровождается возрастанием энтропии.
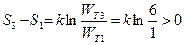 .
.
Обратный самопроизвольный процесс «запрещен» вторым законом термодинамики, так как в нем энтропия убывает  .
.
Можно оценить соотношение термодинамических вероятностей для реальных процессов. Оценим, например, вероятность того, что 1 моль газа самопроизвольно соберется в одной половинке занимаемого им объёме. Изменение энтропии в таком процессе представимо двумя соотношениями:
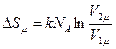 и
и  .
.
Поскольку  , получим:
, получим: 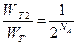 . Число Авогадро равно
. Число Авогадро равно 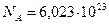 частиц/моль, так что процесс чрезвычайно маловероятен.
частиц/моль, так что процесс чрезвычайно маловероятен.
Данные работы Больцмана раскрыли статистический характер второго закона термодинамики, важность флуктуаций, как реализация кратковременных самопроизвольных отклонений систем от равновесного состояния. Эта флуктуационная гипотеза значительно ослабляла позиции «теории тепловой смерти Вселенной», развиваемой последователями Клаузиуса. Клаузиус, распространяя законы термодинамики на Вселенную, как целое, утверждал: «Энергия мира остается постоянной, энтропия мира стремится к максимуму». Такое утверждение предполагает наступление всеобщего равновесия с прекращением всех процессов, т.е. к «тепловой смерти мира».
Третий закон термодинамики был сформулирован в результате исследования различных свойств термодинамических систем в области низких температур, т.е. при температурах, стремящихся к абсолютному нулю. Его можно сформулировать в виде: «при приближении температуры любой равновесной термодинамической системы к абсолютному нулю, ее энтропия стремится к нулю». Наиболее широкие экспериментальные исследования были проведены В.Г. Нернстом, и им было сформулировано утверждение: « абсолютный нуль недостижим» (1906 г.). Это утверждение, фактически, было положено в более позднюю формулировку третьего закона термодинамики. Более подробно эти вопросы Вы будите рассматривать в куре теоретической физики. Сейчас же мы приведем лишь некоторые следствия этого закона.
1). Температурный коэффициент объёмного расширения при 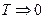 стремится к нулю
стремится к нулю 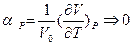 .
.
2). Температурный коэффициент давления при 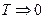 стремится к нулю
стремится к нулю
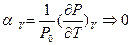 .
.
3). Теплоемкости 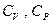 при
при 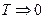 стремятся к нулю.
стремятся к нулю.