 |
|
Исследование функций с помощью производной
Теорема 1. Если функция f дифференцируема в точке x0 и f¢ (x0)>0 (f¢(x0)<0), то f возрастает (убывает) в точке x0.
Теорема 2 (признак постоянства функции). Пусть функция f определена и непрерывна на [a;b] и дифференцируема на (a;b). Для того, чтобы f(x) была постоянной на [a;b] необходимо и достаточно, чтобы f¢(x)=0 "xÎ(a;b).
Теорема 3 (признак монотонности функции). Пусть функция f определена и непрерывна на [a;b] и дифференцируема на (a;b). Функция не убывает (не возрастает) на [a;b] Û f¢ (x)³0 (f¢ (x)£0) на (a;b).
Теорема 4. Пусть функция f определена и непрерывна на [a;b] и дифференцируема на (a;b). Если f¢ (x)>0 (f¢(x)<0), то f возрастает (убывает) на (a;b).
Определение 1.Точка х=х0 называется точкой максимума функции f, если существует окрестность  ÌV(x0), в пределах которой выполнено неравенство f(x)£f(x0).
ÌV(x0), в пределах которой выполнено неравенство f(x)£f(x0).
Значение функции в точке x0 называется максимумом функции.
Определение 2.Точка х=х0 называется точкой минимума функции f, если существует окрестность  ÌV(x0): "xÎ
ÌV(x0): "xÎ  выполнено f(x)³f(x0).
выполнено f(x)³f(x0).
Значение функции в точке x0 называется минимумом функции.
Теорема 5 (необходимое условие экстремума). Пусть f(x) определена в V(x0). Если функция имеет в точке x0 экстремум, то производная функции в этой точке равна нулю или не существует.
Определение. Пусть f(x) определена в V(x0). Точка x0 называется стационарной точкой функции f, если f ¢(x0)=0. Точка x0 называется критической точкой функции f, если f ¢(x0)=0 или не существует.
Теорема 6 (первое достаточное условие экстремума). Пусть f дифференцируема в некоторой окрестности точки x0, кроме, быть может, самой точки x0, в которой она непрерывна. Пусть f ¢(x) сохраняет знак в отдельности как слева, так и справа от точки x0, т. е. в интервалах (x0-d; x0), (x0;x0-d). Если:
1) f ¢(x)>0 при x<x0 и f ¢(x)<0 при x>x0, то x=x0 - точка строгого максимума;
2) f ¢(x)<0 при x<x0 и f ¢(x)>0 при x>x0, то x=x0 - точка строгого минимума;
3) f ¢(x)>0 или f ¢(x)<0 "xÎV(x0), то x=x0 не является точкой экстремума.
Алгоритм нахождения точек экстремума для функции, непрерывной на <a;b>
Пусть f(x) на <a;b> имеет несколько критических точек. Расположим их в порядке возрастания: a<x1<x2<…<xn<b. Они делят <a;b> на интервалы (а;x1), (x1;x2),…,(xn;b). В каждом из них f ¢(x0)¹0, она знакопостоянна (положительна, или отрицательна). Для определения знака производной в интервале надо определить ее знак в любой точке интервала. Затем по изменению знака производной при переходе от одного интервала к другому определим точки экстремума по теореме 6.
Нахождение наибольшего и наименьшего значений функции на отрезке
Пусть функция f(x) дифференцируема на отрезке [a;b]. Тогда она непрерывна на этом отрезке и, в силу II – й теоремы Вейерштрасса, достигает на нем наибольшего и наименьшего значений. Если функция имеет наибольшее значение на (a;b), то это – один из максимумов. Но функция может иметь наибольшее значение и на концах отрезка [a;b]. Аналогичные рассуждения – для минимума. Значит, для нахождения наибольшего и наименьшего значений функции на отрезке [a;b] надо:
1) найти все критические точки функции, принадлежащие отрезку [a;b];
2) вычислить значения функции в этих точках и на концах отрезка;
3) из полученных значений выбрать наибольшее и наименьшее.
Определение. Функция f(x) называется выпуклой вверх (вниз) на <a;b>, если график функции в пределах <a;b> лежит не выше (не ниже) любой из своих касательных.
Теорема 6. Пусть функция f(x) дважды дифференцируема на <a;b>. Тогда если f ²(x)³0 (f ²(x)£0) на (a;b), то функция выпукла вниз (вверх) на <a;b>.
Определение.Точка x0 называется точкой перегиба функции f(x), если при переходе через эту точку меняется направление выпуклости функции f(x).
В примере х=0 – точка перегиба.
Теорема 7 (необходимое условие перегиба). Если в точке перегиба x0 функции f(x) вторая производная существует и непрерывна, то она в этой точке равна нулю.
Теорема 8(первое достаточное условие перегиба). Пусть функция f(x) дважды дифференцируема в  , где x0 – точка возможного перегиба. Если
, где x0 – точка возможного перегиба. Если
1) f ²(x) меняет знак при переходе через x0, то x0 - точка перегиба функции f(x);
2) f ²(x) не меняет знака при переходе через x0, то x0 не является точкой перегиба функции f(x).
Задание №1.
Найти дифференциалы функций:
1. 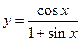
2. 
3. 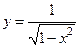
4. 
5. 
6. 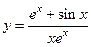
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
Задание №2.
Найти производную второго порядка функции:
1.  3.
3.  5.
5. 
2.  4.
4. 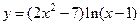
Задание №3.
Составить уравнения касательной и нормали к графику функции y=f(x) в точке с абсциссой x0:
1.  , x0=-14.
, x0=-14.  , x0=27.
, x0=27.  , x0=1
, x0=1
2. 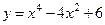 x0=-1 5.
x0=-1 5.  , x0=38.
, x0=38.  , x0=5
, x0=5
3. 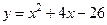 x0=4 6.
x0=4 6.  , x0=0 9.
, x0=0 9.  , x0=-2
, x0=-2
Задание №4.
Найти наибольшее и наименьшее значения функции на отрезке:
1.  , [0;4]
, [0;4]
2.  , [-2;1]
, [-2;1]
3. 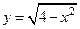 , [-2;2]
, [-2;2]
4.  ,
, 
5.  ,
, 
6. 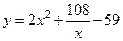 [2;4]
[2;4]
7.  , [-1;7]
, [-1;7]
8. 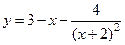 , [-1;2]
, [-1;2]
9.  , [-1;6]
, [-1;6]
10.  , [-4;-1]
, [-4;-1]
11.  , [2;4]
, [2;4]
12.  , [1;9]
, [1;9]
13.  , [-4;2]
, [-4;2]
14.  , [0;4]
, [0;4]
Задание №5.
Исследовать функцию на монотонность и выпуклость, найти экстремумы и точки перегиба:
1.  6.
6. 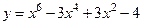 11.
11. 
2.  7.
7.  12.
12. 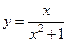
3.  8.
8.  13.
13. 
4.  9.
9. 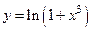
5.  10.
10. 