Главная | Обратная связь

Образцы выполнения заданий

Задание №1

Пример.

Найти дифференциал функции .

Решение.

Перепишем функцию в виде . Воспользуемся правилом дифференцирования произведения: (uv)¢=u¢v+uv¢.

.

Тогда .

Задание №2

Пример.

Найти производную второго порядка функции .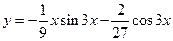

Решение.

Применяя правила дифференцирования, получим

.

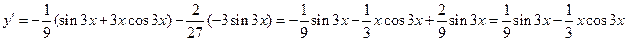Для нахождения второй производной надо продифференцировать первую производную:

.

 

Задание №3

Пример.

Составить уравнения касательной и нормали к графику функции в точке с абсциссой x₀=1.

Решение.

Уравнение касательной к графику функции y=f(x) в точке с абсциссой x₀ имеет вид

.

Вычислим значение функции в данной точке: .

Найдем производную функции и ее значение в данной точке:

, .

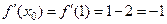Подставим найденные значения в уравнен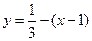ие касательной:

, - уравнение касательной.

Уравнение нормали к графику функции y=f(x) в точке с абсциссой x₀ имеет вид

.

Подставим найденные значения в это уравнение:

, - уравнение нормали.

Задание №4

 

Пример.

Найти наибольшее и наименьшее значения функции на отрезке [2;5].

Решение.

1) Найдем критические точки функции.

,

f ¢(x)=0 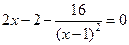Û 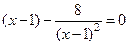Û Û .

На отрезке [2;5] знаменатель не обращается в нуль. Следовательно, дробь равна нулю тогда и только тогда, когда числитель равен нулю:

(x-1)³-8=0 Û (x-1)³=8 Û x-1=2 Û x=3.

Значит, х=3 – критическая точка функции. Она принадлежит данному отрезку.

Найдем значение функции в критической точке: .

2) Найдем значения функции на концах отрезка:

, .

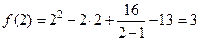3) Из полученных значений выбираем наибольшее и наименьшее:

, .

 

Задание №5

Пример 1.

Исследовать функцию 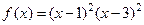на монотонность и выпуклость, найти экстремумы и точки перегиба.

Решение.

1) Найдем область определения функции.

D(f)= , т. к. данная функция – многочлен.

2) Исследуем функцию на монотонность, найдем точки экстремума.

Найдем вначале критические точки функции.

.

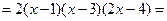
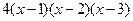D(f¢ )= , т. к. производная тоже является многочленом.

f ¢(x)=0 Û x=1 или х=2 или х=3. Следовательно, x=1, х=2, х=3 – критические точки функции.

Нанесем критические точки функции на числовую прямую и определим знаки производной в каждом из получившихся промежутков.

На промежутках

(-¥;1], [2;3] функция убывает, на промежутках [1;2], [3;+¥) функция возрастает.

Точки х=1 и х=3 – точки минимума функции, min f(x)=f(1)=f(3)=0.

Точка х=2 – точка максимума функции, max f(x)=f(2)=1.

3) Исследуем функцию на выпуклость, найдем точки перегиба.

f ¢¢(x)=4((x-2)(x-3)+(x-1)(x-3)+(x-1)(x-2))=4(x²-5x+6+x²-4x+3+x²-3x+2)=4(3x²-12x+11).

f ¢¢(x)=0 Û 3x²-12x+11=0 Û .

Нанесем точки х₁ и х₂ на числовую прямую и определим знаки второй производной в каждом из получившихся промежутков.

На промежутках и функция выпукла вниз, на промежутке функция выпукла вверх. Точки и являются точками перегиба.