Главная | Обратная связь

Графическая иллюстрация

Производная, основные определения и понятия.

В этой статье дадим основные понятия, на которых будет базироваться вся дальнейшая теория по теме производная функции одной переменной.

Путь x – аргумент функции f(x) и 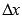- малое число, отличное от нуля.

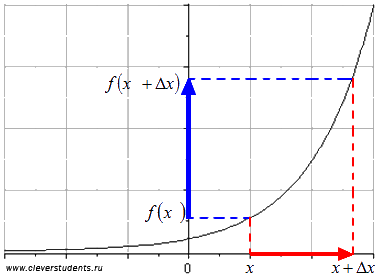
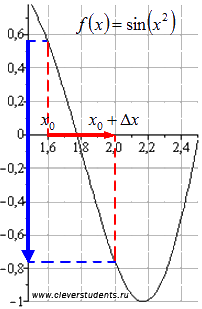
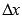(читается «дельта икс») называют приращением аргумента функции. На рисунке красной линией показано изменение аргумента от значения x до значения (отсюда видна суть названия «приращение» аргумента).

При переходе от значения аргумента 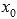к 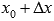значения функции изменяются соответственно от до 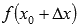при условии монотонности функции на отрезке . Разность называют приращением функции f(x), соответствующем данному приращению аргумента. На рисунке приращение функции показано синей линией.

Рассмотрим эти понятия на конкретном примере.

Возьмем, к примеру, функцию 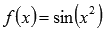. Зафиксируем точку 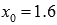и приращение аргумента . В этом случае приращение функции при переходе от 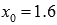к 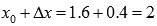будет равно

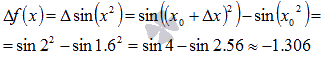
Отрицательное приращение 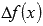говорит об убывании функции на отрезке .

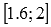Графическая иллюстрация

Определение производной функции в точке.

Пусть функция f(x) определена на промежутке (a; b), 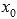и 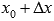- точки этого промежутка.Производной функции f(x) в точке 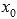называется предел отношения приращения функции к приращению аргумента при 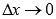. Обозначается .

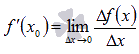Когда последний предел принимает конкретное конечное значение, то говорят о существовании конечной производной в точке. Если предел бесконечен, то говорят, чтопроизводная бесконечна в данной точке. Если же предел не существует, то и производная функции в этой точке не существует.

Функцию f(x) называют дифференцируемой в точке 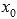, когда она имеет в ней конечную производную.

Если функция f(x) дифференцируема в каждой точке некоторого промежутка (a; b), то функцию называют дифференцируемой на этом промежутке. Таким образом, любой точке x из промежутка (a; b) можно поставить в соответствие значение производной функции в этой точке , то есть, мы имеем возможность определить новую функцию , которую называют производной функции f(x) на интервале (a; b).

Операция нахождения производной называется дифференцированием.

Проведем разграничения в природе понятий производной функции в точке и на промежутке: производная функции в точке – это есть число, а производная функции на промежутке – это есть функция.

Давайте разберем это на примерах для ясности картины. При дифференцировании будем пользоваться определением производной, то есть переходить к нахождению пределов. При возникновении трудностей рекомендуем обращаться к разделу теории пределы, основные определения, примеры нахождения, задачи и подробные решения.

Пример.

Найти производную функции 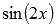в точке 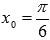, используя определение.

Решение.

Так как мы ищем производную функции в точке, то в ответе должно быть число. Запишем предел отношения приращения функции к приращению аргумента и воспользуемся формулами тригонометрии:

Осталось применить первый замечательный предел для получения конечного результата:

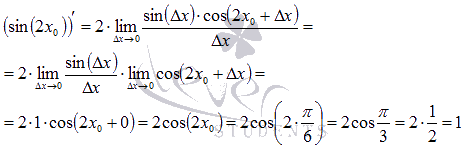
Ответ:

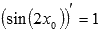
Пример.

Найдите производную функции 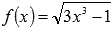на промежутке 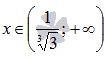, пользуясь определением.

Решение.

Так как мы ищем производную функции на интервале, то в ответе должна получиться функция. Возьмем 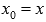, где x – любое число из промежутка 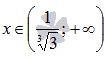. По определению, производная есть предел отношения приращения функции к приращению аргумента, при приращении аргумента, стремящемся к нулю:

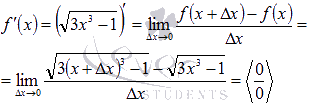
Таким образом, пришли к неопределенности. Для нахождения подобных пределов используют домножение на сопряженное выражение с последующим применением формул сокращенного умножения, приведением подобных слагаемых и сокращением:

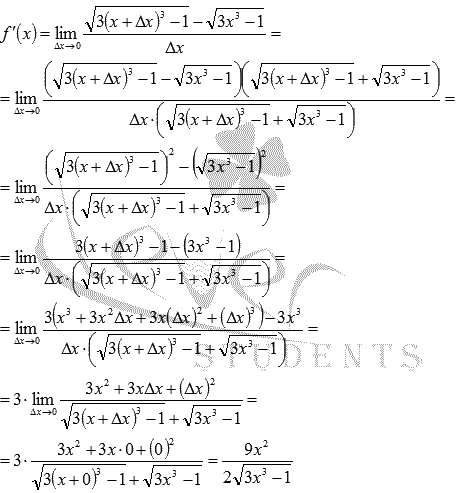
Ответ:

при .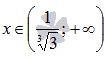

Давайте еще остановимся на одном очень важном моменте: область определения функции f(x)далеко не всегда совпадает с областью определения производной. Заметьте, в предыдущем примере областью определения исходной функции является промежуток , а производная определена на интервале . Что мы хотим этим сказать. Да то, что при дифференцировании в идеале ответ звучит так: функция является производной функции f(x) на промежутке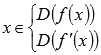

На основании определения производной получены многие формулы таблицы производныхосновных элементарных функций, которые очень ускоряют дифференцирование. Понятие производной также используется при доказательстве правил дифференцирования.