Главная | Обратная связь

ВРАЩАТЕЛЬНЫЕ МОЛЕКУЛЯРНЫЕ СПЕКТРЫ

Энергию вращательного движения молекулы выражают уравнением

, (1)

где I - момент инерции, кг×м²; h - постоянная Планка, h = 6,625×10^-34; j - враща­тельное квантовое число 0, 1, 2, 3, 4 и т.д.; e_вр - энергия вращательного движения, Дж.

Если принять, что при вращении параметры молекулы остаются посто­янными I = const, то уравнение (1) можно записать:

e_вр = В×j( j + 1),

где - вращательная постоянная, Дж.

Если молекула переходит из состояния, характеризуемого враща­тельным квантовым числом j', в состояние с вращательным квантовым чис­лом j", то

.

Так как Dj по правилу отбора может быть равно +1 или - 1, то в спектре поглощения Dj = +1, j' - j" = 1, и тогда

 

.

 

 

Энергия De_вр, расходуемая на увеличение скорости вращательного движе­ния, поглощается из потока квантов света, падающего на вещество; и в спектре света, прошедшего через вещество, наблюдается появление целого ряда максимумов поглощения. Энергию квантов света, соответствующую максимуму поглощения, можно приравнять к изменению энергии вращатель­ного движения молекул:

 

De_вр = h×c×w,

откуда

 

;

 

w = B'(j'+ 1), (2)

где - вращательная постоянная, м^-1; с - скорость света, м/с,

с = 3×10⁸ ;

 

Момент инерции I равен сумме произведений масс m на квадрат расстояния их от оси вращения r:

,

где i – атомность молекулы.

Для несимметричной двухатомной молекулы

I = m₁r₁² + m₂r₂².

При свободном вращении m₁r₁ = m₂r₂, и если обозначить r₁ + r₂ = r₀, где r₀ - длина связи или расстояние между центрами тяжести атомов, то

; ;

 

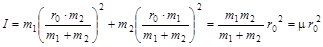, (3)

 

где m - приведенная масса, которая может быть выражена через атомные массы:

 

, (4)

где A₁ и A₂ – атомные массы; m_C - масса атома углерода; m_C/12 = 1,66×10^-27 кг.

Из уравнений (2) и (3) следует, что

,

откуда

r₀ = (I/m)^1/2 = (h/4×p²×B'×c)^1/2 = (h/B'×c)^1/2 / (2p).

Значение В' можно определить по разности волновых чисел соседних максимумов поглощения:

w₁ = B'(j + 1); w₂ = B'j;

 

Dw = w₁ - w₂ = B'.

Поглощение света с возбуждением вращательного движения возможно только в том случае, если молекула имеет постоянный дипольный момент.

Пример

Рассчитать волновое число во вращательном спектре поглощения ¹⁹F-⁷⁹Br, которое соответствует переходу с вращательного квантового уровня j = 1 на уровень j = 2, если межъядерное расстояние r₀ = 1,7555×10^-10 м.

 

Решение

Волновое число полосы поглощения во вращательном спектре можно определить по уравнению (2). Для этого необходимо вычислить вра­щательную постоянную В'. Момент инерции вычислим по уравнению (3), приведенную массу- по уравнению (4):

;

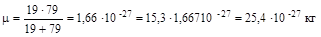I = 25,4×10^-27(1,7555×10^-10)² = 78,355×10^-47 кг×м².

Тогда

.

w = 71,4×2 = 142,8 м^-1.

Задание

По данным вращательных спектров определены разности волновых чи­сел соседних полос поглощения или вращательных линий комбинационного рассеяния. Рассчитать момент инерции и межъядерное расстояние для мо­лекулы А.

Номер варианта	А	Dw×10-2, м-1	Номер варианта	А	Dw×10-2, м-1
	H - Н N - N O - O F - F Na - Na P- P S - S Cl - Cl K - K Br - Br I - I H - F D* - F	121,600 4,020 2,900 2,160 0,310 0,606 0,590 0,490 0,112 0,162 0,075 41,880 31,400		H-35Cl H-37Cl D-Cl H-Br D-Br H-I D-I C-O N-O H-O D-O T**-O	20,880 20,850 10,700 16,710 8,460 12,840 6,420 3,860 3,420 37,740 20,200 14,200

*D - дейтерий

**T - тритий

 

Занятие 3