Короткі теоретичні відомості

Лабораторна робота №2

ВИЗНАЧЕННЯ ЕНЕРГІЇ АЛЬФА-ЧАСТИНОК

ПО ЇХ ПРОБІГУ В ПОВІТРІ

Мета роботи: визначення енергії альфа-частинок по довжині їх пробігу в повітрі.

Короткі теоретичні відомості

Альфа-розпадом називається самодовільне ядерне перетворення, при якому заряд ядра зменшується на 2, а масове число — на 4. Він супроводжується випромінюванням альфа-частинки, тобто ядра атому .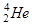

Як приклад наведемо розпад , реакція перетворення якого

Альфа-розпад спостерігається в атомних ядрах з порядковими номерами Z > 82. Їх періоди напіврозпаду охоплюють межі від 10^-7 с до 10¹⁵ років і більше. На сьогоднішній день відомо більше двохсот альфа-активних ядер, більшість з яких отримують штучно. Енергетичний спектр альфа-частинок дискретний (лінійчатий), бо енергетичні стани вихідного (материнського) та кінцевого (дочірнього) ядер є дискретними. Енергії a-частинок різних ядер мають значення від 3-4 до 9 МеВ.

Рис. 8. Енергія взаємодії альфа-частинки з остаточним ядром

У випадку 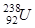Е_a = 4.21 МеВ, а висота потенціального бар’єру для альфа-частинки 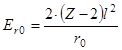, якщо прийняти висоту потенціального бар’єру рівною кулонівському потенціалу на відстані r₀ від центру ядра. Для Е_r0 = 25 МеВ. Це справедливо, якщо a-частинка вилітає з ядра з орбітальним моментом l = 0. Можливі випадки, коли l відрізняється від нуля. Якщо , то крім кулонівського бар’єру необхідно врахувати ще так званий відцентровий бар’єр: 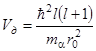. Таким чином, повна висота бар’єру або повний потенціал взаємодії альфа-частинки з ядром

Підставляючи чисельні значення величин, знаходимо 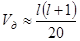МеВ, тобто при зміні l від 5 до 10 V_д змінюється від 1.5 до 5.5 МеВ — висота бар’єру визначається в основному кулонівським потенціалом. Згідно з класичною механікою, альфа-частинка може залишити ядро тільки тоді, коли її енергія перевищує висоту потенціального бар’єру. Тому у випадку класична механіка стає в глухий кут, оскільки при значенні енергії 4.21 МеВ альфа-частинка повинна була би навіки залишитися замкненою всередині ядра. Квантова механіка дає вихід з цього положення. В 1928 р. Гамов, Герні та Кондон створили теорію, яка стверджує, що альфа-частинка має скінчену ймовірність проникнути через потенціальний бар’єр за допомогою “тунельного ефекту”, навіть якщо її енергія значно менша за висоту бар’єру. Ця ймовірність зростає зі збільшенням енергії частинки. Для Е_a < 4 МеВ проникність бар’єру дуже мала, а отже, ймовірність випускання ядром альфа-частинки незначна. Це пояснює ту обставину, що серед відомих альфа-активних ядер жодне не випромінює альфа-частинки за енергією, яка менше за 4 МеВ.

Квантова теорія виходить з рівняння Шредінгера, яке визначає хвильову функцію альфа-частинки, що знаходиться в полі. Потенціал цього поля зображено на рис. 8. Альфа-частинка, що виходить з ядра з енергією E₂ має більшу ймовірність тунелювання крізь кулонівський бар’єр, ніж альфа-частинка з меншою енергією E₁. Заштрихована на малюнку площа більша для частинки з E₁.

При цьому розглядається плоска хвиля, яка падає збоку на потенціальний бар’єр. Вона частково відбивається, а частково проходить. Ймовірність Р проходження частинки через потенціальний бар’єр дорівнює відношенню потоку, що пройшов, до потоку, що падає:

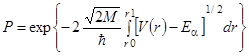де М — приведена маса альфа-частинки та остаточного ядра, а 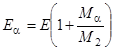— кінетична енергія альфа-частинки в лабораторній системі координат ( M_a — маса альфа-частинки, M₂ — маса остаточного ядра ).

Добуток частоти коливань альфа-частинки всередині ядра на ймовірність Р ( прозорість потенціального бар’єру ) дає ймовірність альфа-розпаду даного ядра в одиницю часу, тобто сталу розпаду l.

Залежність кількості альфа-частинок від їх повного пробігу дозволяє визначити середній або екстрапольований пробіг та по ньому знайти енергію частинок. Таким чином, задача визначення енергії альфа-частинок зводиться до експериментального визначення залежності кількості зареєстрованих альфа-частинок від відстані між джерелом та детектором.

На рис. 9 показано графік залежності кількості альфа-частинок N_αз однаковими початковими енергіями в залежності від відстані від джерела х для колімованого пучка. Там же пунктирною кривою зображено розподіл альфа-частинок по пробігах, який отримано диференціюванням попередньої залежності. Максимум розподілу відповідає значенню пробігу, що дорівнює R₀ та називається середнім пробігом. Він співпадає з відстанню, яку проходить половина всіх частинок.

Рис. 9. Залежність кількості (N) моноенергетичних альфа-частинок від шляху x, який вони пройшли від джерела в колімованому пучку, та розподіл частинок по пробігах (dN/dx); а — випадок неколімованого пучка альфа-частинок

Для альфа-частинок, які виникають при розпаді ядер, середній пробіг в повітрі при нормальних умовах лежить в межах приблизно від 3 до 7 см. Він пов’язаний з кінетичною енергією альфа-частинок Е_α співвідношенням

. (1)

Функція N(x) спадає досить швидко на рис. 9, але такий вигляд вона має тільки для випадку колімованого пучка частинок. Колімація здійснюється шляхом проходження альфа-частинок через серію отворів. У випадку неколімованого пучка, залежність спадає N(x) більш повільно, бо при колімації кількість частинок зменшується не декілька порядків. Екстраполяція спадаючої ділянки на вісь абсцис дає значення кількості частинок, яке дорівнює R₀ ( рис. 9, крива а). У випадку пучка альфа-частинок, що розходиться, збільшення відстані між радіоактивним препаратом та лічильником (тобто зменшення тілесного кута) призводить до того, що зменшується кількість частинок, що потрапила до детектору. Тому треба до результатів вимірів включити поправку на тілесний кут. Реєстрація випромінювання здійснюється , як правило, детектором з круглим вхідним вікном, радіус якого обмежений або його конструкцією, або радіусом та розташуванням діафрагми, яка знаходиться між ним та джерелом. Визначення поправки на тілесний кут ω проводиться розрахунком за геометричними розмірами приладу. Ця поправка вказана в таблиці 1, де h — відстань між джерелом та лічильником, r —радіус віконця радіоактивного джерела, а r₀ — радіус віконця детектору:

Таблиця 3.Поправки на тілесний кут

h/r₀	r/r₀
0,0	0,25	0,50	0,75	1,0	1,25	1,50
0,0	0,500	0,500	0,500	0,500	0,500	0,320	0,227
0,1	0,450	0,449	0,445	0,428	0,419	0,286	0,213
0,2	0,402	0,400	0,392	0,364	0,345	0,253	0,187
0,4	0,314	0,312	0,300	0,264	0,240	0,197	0,159
0,5	0,276	0,273	0,262	0,330	0,206	0,175	0,145
0,6	0,246	0,242	0,229	0,190	0,181	0,158	0,133
0,8	0,188	0,185	0,176	0,155	0,143	0,127	0,112
1,0	0,146	0,145	0,138	0,122	0,115	0,102	0,0870
1,25	0,144	0,143	0,0985	0,0960	0,0874	0,0800	0,0635
1,5	0,0810	0,0809	0,0778	0,0750	0,0700	0,0647	0,0584
1,75	0,0645	0,0644	0,0627	0,0610	0,0568	0,0536	0,0492
2,0	0,0527	0,0525	0,0511	0,0501	0,0466	0,0468	0,0424
2,5	0,0354	0,0353	0,0348	0,0332	0,0326	0,0320	0,0302
3,0	0,0256	0,0255	0,0250	0,0242	0,0240	0,0238	0,0230
3,5	0,0197	0,0196	0,0190	0,0188	0,0186	0,0180	0,0174
4,0	0,0150	0,0149	0,0146	0,0145	0,0143	0,0142	0,0140
5,0	0,0098	0,0097	0,0097	0,0095	0,0095	0,0094	0,0092

Рис. 10. Пояснення до введення поправки на тілесний кут

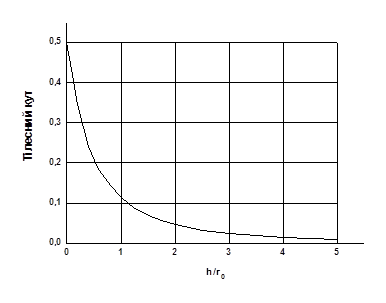
Рис. 11. Залежність поправки на тілесний кут ω від співвідношення h/r₀ для r/r₀ = 1

12 Следующая ⇒