 |
|
Интегрирование функций
Типовой расчет по теме «функциональные ряды».
Пример 1. Найти область сходимости ряда

Решение. К этому ряду формула (4.39) неприменима, так как отсутствуют четные степени переменной  , т.е.
, т.е.  ,
,  , 2, 3,
, 2, 3, 
Применяем непосредственно признак Даламбера:

 .
.
Данный ряд сходится для 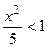 , или
, или 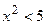 , т.е.
, т.е. 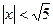 , следовательно,
, следовательно,  . Проверим сходимость на концах интервала. При
. Проверим сходимость на концах интервала. При  получаем ряды
получаем ряды
 ,т.е.
,т.е. 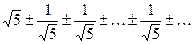 , которые, очевидно, расходятся.
, которые, очевидно, расходятся.
Следовательно, областью сходимости будет  .
.
Пример 2. Найти область сходимости ряда


Решение. По формуле (4.40) имеем
 ,
,
т.е.  , ряд сходится в интервале
, ряд сходится в интервале  . Исследуем ряд на сходимость в концах интервала. При
. Исследуем ряд на сходимость в концах интервала. При  получаем числовой ряд
получаем числовой ряд
 ,
,
который исследуем с помощью необходимого признака сходимости рядов. Имеем
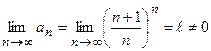 ,т.е. общий член ряда не стремится к нулю и ряд расходится. При
,т.е. общий член ряда не стремится к нулю и ряд расходится. При  получаем числовой ряд
получаем числовой ряд
 , который по признаку Лейбница для знакочередующихся рядов расходится, т.к. не выполняется условие
, который по признаку Лейбница для знакочередующихся рядов расходится, т.к. не выполняется условие  .
.
Итак, окончательно имеем: областью сходимости будет промежуток  .
.
Пример 3. Найти радиус сходимости ряда

Решение. К этому ряду неприменима формула (4.39), так как отсутствуют нечетные степени переменной  , т.е.
, т.е.  ,
,  Применяем непосредственно признак Даламбера:
Применяем непосредственно признак Даламбера:


 ,
,
при любом x, т.е. ряд сходится на всей числовой прямой.
Задача1
Исследовать сходимость следующих степенных рядов. Найти их области сходимости.
1.01  ;
; 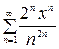 . 1.02
. 1.02  ;
;  . 1.03
. 1.03  ;
;  .
.
1.04  ;
;  .1.05
.1.05  ;
;  . 1.06
. 1.06  ;
;  .
.
1.07  ;
;  .1.08
.1.08  ;
;  .1.09
.1.09 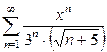 ;
;  .
.
1.10  ;
;  . 1.11
. 1.11 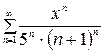 ;
;  1.12
1.12  ;
;  .
.
1.13  ;
;  .1.14
.1.14 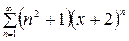
 ;1.15
;1.15 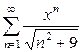 ;
;  .
.
1.16  ;
;  . 1.17
. 1.17  ;
;  . 1.18
. 1.18 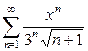 ;
;  .
.
1.19  ;
;  . 1.20
. 1.20  ;
;  1.21
1.21  ;
;  .
.
1.22  ;
; 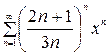 .1.23
.1.23  ;
;  . 1.24
. 1.24  ;
;
Примеры практического применения
степенных рядов
 .1.25
.1.25  ;
;  .
.
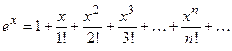 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)

 (5)
(5)
 (6)
(6)
1.Вычисление значений функций
Пример1.Вычислить число  , т.е. значение функции
, т.е. значение функции  при
при  , с точностью до 0,001 (если известно, что
, с точностью до 0,001 (если известно, что 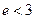 ).
).
Решение. Имеем

Тогда
 ,
,
причем абсолютная погрешность этого приближения равна
 , где
, где  . При
. При  получаем
получаем  .
.
При этом  , где
, где  ,
,
но так как  , то
, то 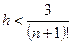 .
.
Число  определим из равенства
определим из равенства  . Откуда
. Откуда  , т.е.
, т.е. 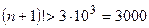 . Если взять
. Если взять  , то
, то  . Возьмем
. Возьмем 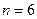 ,
,  .
.
Следовательно,



 .
.
Интегрирование функций
Пример 2. При изучении теории вероятности важную
роль играет функция  ,
,
называемая функцией Лапласа, или интегралом вероятностей. Вычислить интеграл непосредственным интегрированием нельзя, так как  не выражается через элементарные функции.
не выражается через элементарные функции.
Заменяя в разложении (1)  на
на  , получаем
, получаем

Это разложение, как и разложение для  , имеет место на всей числовой оси, поэтому его можно почленно интегрировать, т.е.
, имеет место на всей числовой оси, поэтому его можно почленно интегрировать, т.е.
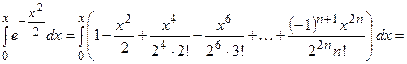

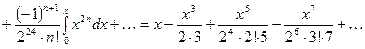

Тогда

 ,
,
сходящимся на всей числовой прямой оси. Вычислить значение функции  очень просто, так как ряд быстро сходится.
очень просто, так как ряд быстро сходится.