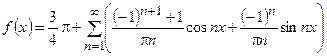|
|
Интегрирование дифференциальных уравнений
Рассмотрим теперь применение рядов Тейлора к решению дифференциальных уравнений. Пусть заданы дифференциальное уравнение и начальные условия, определяющие частное решение. Допустим, что решение уравнения в окрестности точки, в которой заданы начальные условия, можно разложить в степенной ряд,
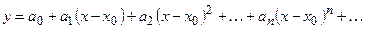
Продифференцируем этот ряд с неопределенными пока коэффициентами столько раз, каков порядок уравнения.
Подставляя затем в уравнение вместо неизвестной функции и ее производных соответствующие ряды, мы получим тождество, из которого и определим неизвестные коэффициенты ряда. При этом первые коэффициенты ряда определяются из начальных условий. Если, далее, доказать, что полученный ряд сходится, то можно быть уверенным, что он выражает искомое решение.
Достаточно большое число членов ряда дает нам как угодно хорошее приближенное выражение решения в виде многочлена.
Рассмотрим указанный метод на примерах.
интегрированием уравнения.
Пример 4. Найти решение дифференциального уравнения  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  .
.
Решение. Это уравнение нелинейное, и поэтому подстановка вместо  его разложения в ряд
его разложения в ряд

привела бы к сложным уравнениям для определения коэффициентов. Поэтому обычно поступают иначе.
Продифференцируем уравнение несколько раз подряд, рассматривая  как функцию от
как функцию от  :
:
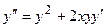 ,
,


 .
.
Подставляя во все уравнения и во все производные  и учитывая начальное условие
и учитывая начальное условие  , последовательно найдем:
, последовательно найдем:
 ,
,  ,
,

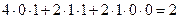 ,
,

 ,
, 
Следовательно, искомое решение записывается в виде ряда Тейлора в точке  .
.
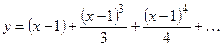
Полученный многочлен в окрестности точки  дает как угодно хорошее приближенное выражение решении.
дает как угодно хорошее приближенное выражение решении.
Задача2 .
Вычислить определенный интеграл с помощью разложения подынтегральной функции в степенной ряд. Обеспечить абсолютную погрешность  :
:
2.01  ; 2.02
; 2.02 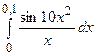 ; 2.03
; 2.03  ;
;
2.04 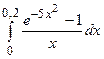 ; 2.05
; 2.05  ; 2.06
; 2.06  ;
;
2.07  ; 2.08
; 2.08  ; 2.09
; 2.09  ;
;
2.10  ; 2.11
; 2.11 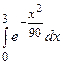 ; 2.12
; 2.12 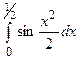 ;
;
2.13  ; 2.14
; 2.14  ; 2.15
; 2.15  ;
;
2.16  ; 2.17
; 2.17  ; 2.18
; 2.18  ;
;
2.19  ; 2.20
; 2.20 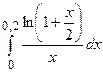 ; 2.21
; 2.21  ;
;
2.22  ; 2.23
; 2.23  ; 2.24
; 2.24  ;
;
2.25  .
.
Задача 3.
Найти первые три числа разложения в степенной ряд решения дифференциального уравнения с заданными условиями.
3.01 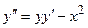 ;
;  ,
,  .
.
3.02  ,
, 
3.03  ,
, 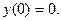
3.04  ,
, 
3.05,  ,
, 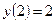 .
.
3.06  ,
,  .
.
3.07  ,
,  .
.
3.08  ;
;  ,
,  .
.
3.09  ;
;  ,
,  .
.
3.10  ,
,  .
.
3.11  ,
,  .
.
3.12 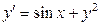 ,
,  .
.
3.13  ,
,  .
.
3.14  ,
, 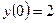 .
.
3.15  ,
,  .
.
3.16  ,
,  .
.
3.17 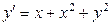
 .
.
3.18  ;
; 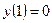 ,
,  .
.
3.19  ;
;  ,
,  .
.
3.20  ,
, 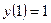 .
.
3.21 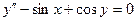 ;
;  ,
,  .
.
3.22 
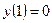 ,
, 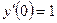 .
.
3.23  ;
;  ,
,  .
.
3.24  ,
, 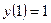 .
.
3.25 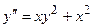 ;
;  ,
,  .
.
Разложение функций в тригонометрические ряды Фурье
1. Разложение в ряд Фурье функций, заданных на отрезке 
Определение 1. Тригонометрический ряд
 , (1)
, (1)
коэффициенты которого совпадают с коэффициентами Фурье для функции  , т.е. вычисляются по формулам
, т.е. вычисляются по формулам
 , где
, где 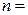 0, 1, 2, 3,
0, 1, 2, 3, 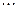 , (2)
, (2)  , где
, где 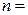 0, 1, 2, 3,
0, 1, 2, 3, 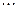 , (3)
, (3)
называются рядом Фурье функции  .
.
 Теорема 1. Если
Теорема 1. Если
функция  кусочно-дифференцируема на отрезке
кусочно-дифференцируема на отрезке 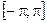 , то ряд Фурье функции
, то ряд Фурье функции  сходится во всех точках
сходится во всех точках  , причем в точках непрерывности функции
, причем в точках непрерывности функции  его сумма равна
его сумма равна  , в точках разрыва функции
, в точках разрыва функции  его сумма равна
его сумма равна 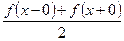 , на концах отрезка его сумма равна
, на концах отрезка его сумма равна  .
.
Пример 1. Разложить функцию  ,
,
 на интервале
на интервале 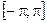 в ряд Фурье.
в ряд Фурье.
Решение. Изобразим функцию графиком.
 Так как функция
Так как функция
 кусочно-дифференци-
кусочно-дифференци-
руема на отрезке  , в силу того, что ее производная
, в силу того, что ее производная
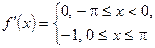 имеет лишь одну точку разрыва
имеет лишь одну точку разрыва  внутри отрезка
внутри отрезка 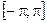 , то ряд Фурье функции
, то ряд Фурье функции  сходится к порождающей его функции во всех точках
сходится к порождающей его функции во всех точках  . При этом значение полученного ряда в концах интервала равно
. При этом значение полученного ряда в концах интервала равно
 .
.
Вычислим коэффициенты Фурье. По формуле (2) имеем


 .
.

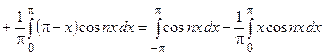 .
.
При вычислении интеграла 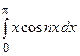 воспользуемся формулой интегрирования по частям
воспользуемся формулой интегрирования по частям
 .
.
Приняв 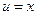 ,
,  , откуда
, откуда 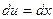 ,
,  .
.
Тогда

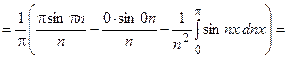
 .
.

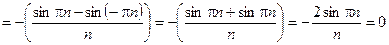 .
.
Окончательно имеем
 .
.
По формуле (3) имеем


 .
.
При вычислении интеграла  воспользуемся формулой интегрирования по частям
воспользуемся формулой интегрирования по частям  . Приняв
. Приняв 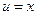 ,
,  , откуда
, откуда 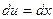 ,
,  .
.
Тогда


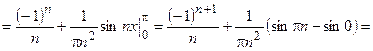
 .
.
Окончательно имеем
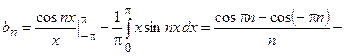
 .
.
Следовательно, функции  соответствует ряд Фурье
соответствует ряд Фурье