 |
|
Векторное произведение векторов.
Упорядоченная тройка некомпланарных векторов называется правой тройкой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против часовой стрелки. В противном случае она называется левой тройкой.
При перестановке в упорядоченной тройке двух любых векторов тройка меняет ориентацию на противоположную.
Векторным произведением 
неколлинеарных векторов 
и 
называется вектор 
, такой что:
· 
;
· 
и 
;
· вектор направлен так, что векторы , и в указанном порядке образуют правую тройку.
В случае, если векторы и коллинеарны, их векторное произведение равно 
.
Левая тройка. Правая тройка.
Свойства векторного произведения:
1°. 
(антикоммутативность).
2°. 
3°. 
(линейность).
Подобно тому, как это было сделано для скалярного произведения, можно получить выражение для векторного произведения векторов через их координаты в заданном базисе. Чтобы записать их в компактной и удобной для запоминания форме, нам потребуется понятие определителя.
Рассмотрим четыре числа: а, b, с и d. Из них можно составить таблицу 
: 
, которая называется квадратной матрицей второго порядка.
Числа а, b , с и d называются элементами матрицы. Элементы a и b образуют первую строку матрицы, элементы c и d — вторую строку; элементы а и с образуют первый столбец матрицы, элементы b и d — второй столбец.
Число ad - bc называется определителем (или детерминантом) матрицы и обозначается так: 
.
Аналогично, таблица 
, составленная из девяти чисел, называется квадратной матрицей третьего порядка.
Как и в случае матрицы второго порядка, вводятся понятия элементов матрицы, ее строк и столбцов. Строки по-прежнему нумеруются сверху вниз, а столбцы — слева направо.
Число 
называется определителем (или детерминантом) матрицы и обозначается 
. Более полная теория матриц и определителей будет дана позже.
Теорема. Пусть 
— правый ортонормированный базис, и в этом базисе 
и 
. Тогда векторное произведение 
вычисляется по следующей формуле = 
.
Доказательство. Так как — правый ортонормированный базис, то 
; 
. Следовательно, 
, 
, 
. Поскольку, во-первых, 
, во-вторых 
, и в-третьих, — правая тройка, то 
. Аналогично, 
, 
, 
, 
, 
. Тогда
=
= 
+ 
+ 
=
= 
+ 
+ 
=
= 
+ 
=
= 
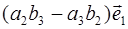
= .ڤ
Теорема. Длина вектора векторного произведения численно равна площади параллелограмма, построенного на векторах и 
, как на смежных сторонах.
Доказательство. 
ڤ
Теорема. Для того чтобы два вектора в пространстве были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось .
Доказательство необходимости. Если векторы и коллинеарны, то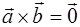 
по определению.
Доказательство достаточности. Пусть 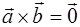. Тогда 
. Если 
или 
, то векторы и коллинеарны, поскольку нулевой вектор коллинеарен любому. Если 
и 
, то 
. Следовательно, 
или 
, то есть векторы и коллинеарны.ڤ