 |
|
ПРЯМАЯ НА ПЛОСКОСТИ
Теорема. Прямая, проходящая через точку  под углом
под углом 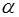 к положительному направлению оси
к положительному направлению оси  (
(  ) имеет уравнение
) имеет уравнение 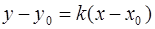 , где
, где  – угловой коэффициент.
– угловой коэффициент.
 Доказательство. Пусть
Доказательство. Пусть  – произвольная точка прямой. Рассмотрим случай
– произвольная точка прямой. Рассмотрим случай  (другой случай рассматривается аналогично). Так как прямые (
(другой случай рассматривается аналогично). Так как прямые ( 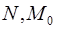 ) и (ОХ)параллельны, то
) и (ОХ)параллельны, то  . Тогда
. Тогда  . Следовательно,
. Следовательно, 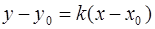 .ڤ
.ڤ
Следствие. Если 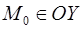 , то есть
, то есть  , то уравнение прямой, проходящей через эту точку под углом
, то уравнение прямой, проходящей через эту точку под углом 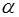 к положительному направлению оси
к положительному направлению оси  (
(  ) имеет уравнение
) имеет уравнение  , где
, где  – угловой коэффициент.
– угловой коэффициент.
Доказательство. Подставим в выведенное уравнение прямой координаты точки  :
: 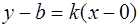 . Тогда
. Тогда  .ڤ
.ڤ
Замечание. Если  , то уравнение прямой, проходящей через точку
, то уравнение прямой, проходящей через точку  , очевидно, имеет вид
, очевидно, имеет вид 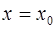 .
.
 Теорема. Прямая, проходящая через две точки
Теорема. Прямая, проходящая через две точки 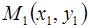 и
и 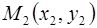 (
(  ,
,  ) имеет уравнение
) имеет уравнение 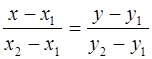 .
.
Доказательство. Пусть  – произвольная точка прямой. Рассмотрим случай
– произвольная точка прямой. Рассмотрим случай  (другой случай рассматривается аналогично). Легко видеть, что
(другой случай рассматривается аналогично). Легко видеть, что  ~
~  (по двум углам). Тогда
(по двум углам). Тогда 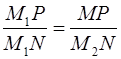 , то есть
, то есть 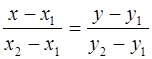 .ڤ
.ڤ
Теорема. Уравнение вида  , где
, где  , есть уравнение прямой, и обратно, любая прямая может быть задана уравнением такого вида.
, есть уравнение прямой, и обратно, любая прямая может быть задана уравнением такого вида.
Доказательство. Пусть дано уравнение  , и пусть
, и пусть  . Тогда это уравнение можно привести к виду
. Тогда это уравнение можно привести к виду  , то есть к виду
, то есть к виду  , про который доказано, что он задает прямую, пересекающую ось OY в точке
, про который доказано, что он задает прямую, пересекающую ось OY в точке  и проходящую под углом
и проходящую под углом 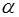 (
(  ) к положительному направлению оси
) к положительному направлению оси  . Если В = 0, то
. Если В = 0, то  . Тогда уравнение можно привести к виду
. Тогда уравнение можно привести к виду  , то есть к виду
, то есть к виду 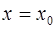 уравнения прямой, пересекающей ось OХ в точке
уравнения прямой, пересекающей ось OХ в точке  и проходящей под углом
и проходящей под углом  к положительному направлению оси
к положительному направлению оси  . Обратно, пусть есть невертикальная прямая. Тогда она имеет уравнение вида
. Обратно, пусть есть невертикальная прямая. Тогда она имеет уравнение вида  . Это уравнение можно привести к виду
. Это уравнение можно привести к виду  , то есть к виду
, то есть к виду  . Если прямая вертикальная, то ее уравнение
. Если прямая вертикальная, то ее уравнение 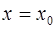 можно привести к виду
можно привести к виду  , то есть к виду
, то есть к виду  .ڤ
.ڤ
 Теорема. Пусть есть две прямые, уравнения которых
Теорема. Пусть есть две прямые, уравнения которых 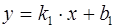 и
и  . Тогда угол между ними (острый) можно получить из формулы
. Тогда угол между ними (острый) можно получить из формулы  .
.
Доказательство. Так как внешний угол 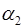 треугольника равен сумме двух углов треугольника, не смежных с ним, то
треугольника равен сумме двух углов треугольника, не смежных с ним, то  , или
, или  . Если
. Если  – острый, то
– острый, то  . Если
. Если  – тупой, то
– тупой, то 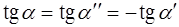 (
(  ). Тогда по определению модуля, по формуле разности тангенсов и определению
). Тогда по определению модуля, по формуле разности тангенсов и определению  и
и  имеем
имеем  =
=  =
= 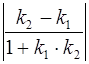 .ڤ
.ڤ
Следствие. Пусть есть две прямые, уравнения которых 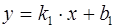 и
и  . Тогда они параллельны, если
. Тогда они параллельны, если 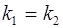 , и перпендикулярны, если
, и перпендикулярны, если  .
.