 |
|
Словарь – СПРАВОЧНИК ОСНОВНЫХ терминов
| ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ | ||||||
| МАТРИЦА | Прямоугольная таблица чисел (элементов матрицы), расположенных в строки и столбцы. Если матрица содержит  строк и строк и  столбцов, то таблица называется матрицей размерностью столбцов, то таблица называется матрицей размерностью 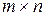 . Матрицы записывают в виде . Матрицы записывают в виде
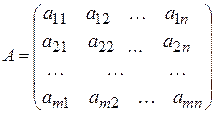 ,
обозначая через ,
обозначая через  ее элемент, находящийся в ее элемент, находящийся в 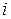 -й строке и -й строке и  -м столбце матрицы, в котором стоит элемент -м столбце матрицы, в котором стоит элемент  . В некоторых случаях размерность матрицы указывают в ее названии: . В некоторых случаях размерность матрицы указывают в ее названии:  . Иногда для матриц используют обозначение . Иногда для матриц используют обозначение  .
Матрица, у которой число строк равно числу столбцов .
Матрица, у которой число строк равно числу столбцов  , называется квадратной матрицей , называется квадратной матрицей  -го порядка. Элементы квадратной матрицы, для которых -го порядка. Элементы квадратной матрицы, для которых 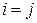 , называют диагональными, а диагональ матрицы, на которой они находятся, - главной диагональю матрицы. , называют диагональными, а диагональ матрицы, на которой они находятся, - главной диагональю матрицы.
| |||||
| ЕДИНИЧНАЯ МАТРИЦА | Квадратная матрица, на главной диагонали которой стоят единицы, а все остальные элементы нулевые. | |||||
ОПРЕДЕЛИТЕЛЬ (детерминант)  -го порядка -го порядка
| Число, которое ставится в соответствие квадратной матрице   -го порядка. Это число обозначается -го порядка. Это число обозначается  , ,  , ,  и вычисляется по определенному закону. Например, определитель второго порядка вычисляется по правилу: и вычисляется по определенному закону. Например, определитель второго порядка вычисляется по правилу:
 . .
| |||||
МИНОР элемента  определителя определителя  -го порядка -го порядка
| Определитель  -го порядка, получаемый из исходного определителя путем вычеркивания из него -го порядка, получаемый из исходного определителя путем вычеркивания из него 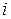 -й строки и -й строки и  -го столбца. Обозначается обычно -го столбца. Обозначается обычно 
| |||||
АЛГЕБРАИЧЕСКОЕ ДОПОЛНЕНИЕ элемента  определителя определителя  -го порядка -го порядка
| Минор  этого элемента, взятый со знаком этого элемента, взятый со знаком  . Обозначение: . Обозначение:  . .
| |||||
| НЕВЫРОЖДЕННАЯ МАТРИЦА | Квадратная матрица с ненулевым определителем. | |||||
ОБРАТНАЯ МАТРИЦА к квадратной матрице 
| Матрица  , для которой справедливо равенство , для которой справедливо равенство  , где , где  - единичная матрица.
Обратная матрица существует только для невырожденных матриц. - единичная матрица.
Обратная матрица существует только для невырожденных матриц.
| |||||
МИНОР k-го порядка матрицы 
| Определитель, который состоит из элементов матрицы, расположенных на пересечении  ее строк и ее строк и  столбцов. столбцов.
| |||||
| РАНГ МАТРИЦЫ | Наивысший порядок минора матрицы, отличного от нуля. | |||||
| УРАВНЕНИЕ | Равенство, в котором одна или несколько букв считаются (называются) неизвестными. | |||||
| ЛИНЕЙНОЕ УРАВНЕНИЕ | Уравнение, содержащее неизвестные (переменные) только в первой степени. Например, уравнение  является линейным уравнением с является линейным уравнением с  неизвестными неизвестными  , ,  ,…. ,….  . .
| |||||
| СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ | Совокупность нескольких линейных уравнений относительно одних и тех же неизвестных. Систему  линейных уравнений с линейных уравнений с  неизвестными можно записать в виде неизвестными можно записать в виде
 Таблица коэффициентов при неизвестных называется матрицей
Таблица коэффициентов при неизвестных называется матрицей  системы,
столбец системы,
столбец  — столбцом неизвестных, а столбец — столбцом неизвестных, а столбец  — столбцом свободных членов.
Если — столбцом свободных членов.
Если  , то определитель матрицы системы называется определителем системы. , то определитель матрицы системы называется определителем системы.
| |||||
| ФОРМУЛЫ КРАМЕРА | Формулы, позволяющие найти решение (единственное) системы  линейных уравнений с линейных уравнений с  неизвестными в случае, если определитель этой системы отличен от нуля. Решение такой системы по формулам Крамера имеет вид: неизвестными в случае, если определитель этой системы отличен от нуля. Решение такой системы по формулам Крамера имеет вид:
 ; ;  ;…… ;……  ,
где ,
где  - определитель системы, а - определитель системы, а 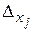 - вспомогательные определители, которые получаются из определителя - вспомогательные определители, которые получаются из определителя  заменой столбца из коэффициентов при заменой столбца из коэффициентов при  столбцом свободных членов. столбцом свободных членов.
| |||||
| МАТРИЧНАЯ ЗАПИСЬ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ | Представление системы  линейных уравнений с линейных уравнений с  неизвестными в виде матричного уравнения неизвестными в виде матричного уравнения
 ,
где ,
где  - матрица системы; - матрица системы;  - столбец неизвестных; - столбец неизвестных;  - столбец свободных членов.
Если - столбец свободных членов.
Если  и матрица и матрица  - невырожденная, то решение системы линейных уравнений определяется по формуле - невырожденная, то решение системы линейных уравнений определяется по формуле
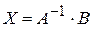 , где , где  - обратная матрица. (Матричный метод решения системы линейных уравнений). - обратная матрица. (Матричный метод решения системы линейных уравнений).
| |||||
| МЕТОД ГАУССА | Метод решения системы  линейных уравнений с линейных уравнений с  неизвестными, основанный на элементарных преобразованиях расширенной матрицы системы уравнений (т.е. матрицы системы, к которой присоединен столбец свободных членов). Элементарными преобразованиями в расширенной матрице называются преобразования, которые не меняют множество решений системы.
Метод Гаусса является универсальным методом решения систем линейных уравнений, который позволяет определить множество всех решений системы (если они есть), либо устанавливает их отсутствие (несовместная система уравнений). неизвестными, основанный на элементарных преобразованиях расширенной матрицы системы уравнений (т.е. матрицы системы, к которой присоединен столбец свободных членов). Элементарными преобразованиями в расширенной матрице называются преобразования, которые не меняют множество решений системы.
Метод Гаусса является универсальным методом решения систем линейных уравнений, который позволяет определить множество всех решений системы (если они есть), либо устанавливает их отсутствие (несовместная система уравнений).
| |||||
| ТЕОРЕМА | Математическое предложение, истинность которого устанавливается или опровергается при помощи доказательства. | |||||
| ТЕОРЕМА КРОНЕКЕРА – КАПЕЛЛИ | Теорема, выражающая необходимое и достаточное условие решения системы  линейных уравнений с линейных уравнений с  неизвестными. Теорема Кронекера – Капели формулируется так: для того, чтобы система неизвестными. Теорема Кронекера – Капели формулируется так: для того, чтобы система  линейных уравнений с линейных уравнений с  неизвестными имела хотя бы одно решение, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы системы. неизвестными имела хотя бы одно решение, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы системы.
| |||||
| ВЕКТОРНАЯ АЛГЕБРА | ||||||
| СКАЛЯРНАЯ ВЕЛИЧИНА (скаляр) | Величина, которая характеризуется только числовым значением. | |||||
| ВЕКТОРНАЯ ВЕЛИЧИНА (вектор) | Величина, которая характеризуется не только числовым значением, но и направлением.
Если выбрать единицу длины, то векторные величины можно изображать геометрическими векторами.
Вектором называется направленный отрезок или упорядоченная пара точек (начало и конец вектора).
На чертеже вектор изображается отрезком прямой, на котором отмечено направление.
Обозначение:  , или , или  (где точка (где точка  - начало вектора, а точка - начало вектора, а точка  – конец вектора). – конец вектора).
| |||||
| НУЛЕВОЙ ВЕКТОР | Вектор, у которого начало и конец совпадают.
Обозначение:  . .
| |||||
| ДЛИНА (МОДУЛЬ) ВЕКТОРА | Расстояние между началом и концом вектора.
Обозначение:  . .
| |||||
| ЕДИНИЧНЫЙ ВЕКТОР (ОРТ) | Вектор, длина которого равна единице. | |||||
| ЛИНЕЙНОЕ (ВЕКТОРНОЕ) ПРОСТРАНСТВО | Множество  называется линейным (векторным) пространством, а его элементы – векторами, если в нем определены действия: называется линейным (векторным) пространством, а его элементы – векторами, если в нем определены действия:
 и и  и любых двух действительных чисел и любых двух действительных чисел  и и  элемент элемент  .
При этом выражение .
При этом выражение  называют линейной комбинацией векторов называют линейной комбинацией векторов  и и  с коэффициентами с коэффициентами  и и  . .
| |||||
| ОСЬ | Прямая, на которой установлено положительное направление.
Любая ось  вполне определяется заданием соответствующего единичного вектора вполне определяется заданием соответствующего единичного вектора  (см. рис.). (см. рис.).
| |||||
| ПРОЕКЦИЯ ТОЧКИ НА ОСЬ | Основание перпендикуляра, опущенного из точки на данную ось. | |||||
| ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ | Проекцией вектора  на ось на ось  называется алгебраическая величина отрезка называется алгебраическая величина отрезка  (см. рис.), где (см. рис.), где  и и  - проекции точек - проекции точек  и и  на данную ось (т.е. длина отрезка на данную ось (т.е. длина отрезка  , взятая со знаком плюс, если направление отрезка совпадает с положительным направлением оси, и со знаком минус – если эти направления противоположны).
Обозначение: , взятая со знаком плюс, если направление отрезка совпадает с положительным направлением оси, и со знаком минус – если эти направления противоположны).
Обозначение:  . .

Если
| |||||
| КООРДИНАТЫ ВЕКТОРА | Координатами вектора  относительно прямоугольной декартовой системы координат относительно прямоугольной декартовой системы координат  называются проекции называются проекции  , ,  , , 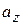 вектора вектора  на взаимно перпендикулярные координатные оси: ось на взаимно перпендикулярные координатные оси: ось  (ось абсцисс), ось (ось абсцисс), ось  (ось ординат), ось (ось ординат), ось  (ось аппликат).
Обозначение: (ось аппликат).
Обозначение:  .
Если .
Если  , ,  , ,  - орты координатных осей - орты координатных осей  , ,  , ,  , то вектор , то вектор  можно представить в виде можно представить в виде
 . .
| |||||
РАДИУС-ВЕКТОР точки 
| Вектор  , идущий от начала координат (точка , идущий от начала координат (точка 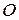 ) к данной точке ) к данной точке  . .
| |||||
| ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ | Система векторов  , , 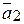 ,…, ,…,  называется линейно зависимой, если существуют такие числа называется линейно зависимой, если существуют такие числа  , ,  ,…, ,…,  , не равные нулю одновременно, что имеет место равенство: , не равные нулю одновременно, что имеет место равенство:
 .
В противном случае система векторов .
В противном случае система векторов  , , 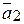 ,…, ,…,  называется линейно независимой.
Выражение называется линейно независимой.
Выражение  называется линейной комбинацией векторов называется линейной комбинацией векторов  , , 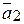 ,…, ,…,  . .
| |||||
| БАЗИС И РАЗМЕРНОСТЬ ЛИНЕЙНОГО ПРОСТРАНСТВА | Линейно независимая система векторов  , , 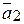 ,…, ,…,  линейного пространства линейного пространства  образует базис, если любые образует базис, если любые 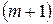 векторов линейного пространства векторов линейного пространства  линейно зависимы.
Количество векторов в базисе линейного пространства линейно зависимы.
Количество векторов в базисе линейного пространства  называется его размерностью.
Обозначение: называется его размерностью.
Обозначение:  ( (  - мерное линейное пространство). - мерное линейное пространство).
| |||||
| КОЛЛИНЕАРНЫЕ ВЕКТОРЫ | Векторы, лежащие на одной прямой или на параллельных прямых. Коллинеарность векторов  и и  обозначают так: обозначают так:    .
Коллинеарные векторы могут иметь одно и то же направление (сонаправленные векторы) и противоположные направления (противоположно направленные векторы). .
Коллинеарные векторы могут иметь одно и то же направление (сонаправленные векторы) и противоположные направления (противоположно направленные векторы).
| |||||
| РАВНЫЕ ВЕКТОРЫ | Сонаправленные векторы с одинаковыми длинами.
Обозначение:  . .
| |||||
| ПРОТИВОПОЛОЖНЫЕ ВЕКТОРЫ | Противоположно направленные векторы с одинаковыми длинами.
Обозначение: вектор, противоположный вектору  , обозначается через , обозначается через  . .
| |||||
| ПЕРПЕНДИКУЛЯРНЫЕ ВЕКТОРЫ | Векторы, угол между которыми (после приведения их к общему началу) равен  . .
| |||||
УСЛОВИЕ КОЛЛИНЕАРНОСТИ двух векторов  и и 
| Для того, чтобы два вектора  и и  были коллинеарны, необходимо и достаточно, чтобы их одноименные координаты были пропорциональны. Например, для векторов были коллинеарны, необходимо и достаточно, чтобы их одноименные координаты были пропорциональны. Например, для векторов  и и  условие коллинеарности имеет вид: условие коллинеарности имеет вид:
 .
Условие коллинеарности двух векторов также можно записать в виде: .
Условие коллинеарности двух векторов также можно записать в виде: 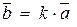 , где , где  . .
| |||||
| КОМПЛАНАРНЫЕ ВЕКТОРЫ | Векторы, лежащие в одной или в параллельных плоскостях. | |||||
| ТРОЙКА ВЕКТОРОВ | Любые три некомпланарных вектора, взятые в определенном порядке.
Обозначение: 
| |||||
| ПРАВАЯ (ЛЕВАЯ) ТРОЙКА ВЕКТОРОВ | Тройка некомпланарных векторов  называется правой (имеющей правую ориентацию), если кратчайший поворот от первого вектора называется правой (имеющей правую ориентацию), если кратчайший поворот от первого вектора  ко второму вектору ко второму вектору  происходит против часовой стрелки, если смотреть из конца третьего вектора происходит против часовой стрелки, если смотреть из конца третьего вектора  .
Если же кратчайший поворот от первого вектора ко второму происходит по часовой стрелке, то тройка некомпланарных векторов называется левой (имеющей левую ориентацию). .
Если же кратчайший поворот от первого вектора ко второму происходит по часовой стрелке, то тройка некомпланарных векторов называется левой (имеющей левую ориентацию).
| |||||
| БАЗИС на плоскости | Любые два неколлинеарных вектора на этой плоскости, взятые в определенном порядке.
Например, орты  и и  координатных осей координатных осей  и и  образуют базис на плоскости. образуют базис на плоскости.
| |||||
| БАЗИС в пространстве | Любые три некомпланарных вектора, взятые в определенном порядке.
Например, орты  , ,  и и  координатных осей координатных осей  , ,  и и  образуют базис в пространстве. образуют базис в пространстве.
| |||||
| РАЗЛОЖЕНИЕ ВЕКТОРА ПО БАЗИСУ | Если на плоскости (или в пространстве) выбран базис, то любой вектор этой плоскости (пространства) можно представить, и притом единственным образом, как линейную комбинацию векторов базиса.
Если  , , 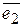 , ,  - базис и вектор - базис и вектор  , то числа , то числа 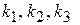 называют координатами вектора называют координатами вектора  в данном базисе, а представление вектора в данном базисе, а представление вектора  в виде в виде  - разложением вектора по данному базису. - разложением вектора по данному базису.
| |||||
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ двух векторов  и и 
| Число, равное произведению длин (модулей) векторов  и и  на косинус угла между ними. Обозначение: на косинус угла между ними. Обозначение:
 ,
где ,
где  , ,  - длины (модули) векторов; - длины (модули) векторов;
 - угол между векторами - угол между векторами  и и  .
Если векторы .
Если векторы  и и  заданы своими прямоугольными декартовыми координатами (в прямоугольном декартовом базисе заданы своими прямоугольными декартовыми координатами (в прямоугольном декартовом базисе  ) : ) :
 , ,  ,
то их скалярное произведение можно вычислить как сумму произведений одноименных координат: ,
то их скалярное произведение можно вычислить как сумму произведений одноименных координат:
 . .
| |||||
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ двух векторов  и и 
| Вектор  , удовлетворяющий следующим условиям: , удовлетворяющий следующим условиям:
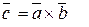 , или , или  .
Если векторы .
Если векторы  и и  заданы своими прямоугольными декартовыми координатами (в прямоугольном декартовом базисе заданы своими прямоугольными декартовыми координатами (в прямоугольном декартовом базисе  ) : ) :  , ,  , то их векторное произведение можно вычислить с помощью определителя: , то их векторное произведение можно вычислить с помощью определителя:
 . .
| |||||
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ трех векторов  , ,  и и 
| Число, равное скалярному произведению вектора  на векторное произведение на векторное произведение 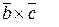 (или скалярное произведение вектора (или скалярное произведение вектора 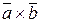 на вектор на вектор  ).
Обозначение: ).
Обозначение: 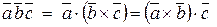 .
Если векторы .
Если векторы  , ,  и и  заданы своими прямоугольными декартовыми координатами (в прямоугольном декартовом базисе заданы своими прямоугольными декартовыми координатами (в прямоугольном декартовом базисе  ): ):  , ,  , ,  , то их смешанное произведение можно вычислить с помощью определителя: , то их смешанное произведение можно вычислить с помощью определителя:
 . .
| |||||
УСЛОВИЕ ОРТОГОНАЛЬНОСТИ двух векторов  и и 
| Для того, чтобы два ненулевых вектора  и и  были ортогональны были ортогональны 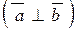 , необходимо и достаточно, чтобы их скалярное произведение равнялось нулю: , необходимо и достаточно, чтобы их скалярное произведение равнялось нулю:
 .
На плоскости и в пространстве ортогональность совпадает с перпендикулярностью векторов. .
На плоскости и в пространстве ортогональность совпадает с перпендикулярностью векторов.
| |||||
УСЛОВИЕ КОМПЛАНАРНОСТИ трех векторов  , ,  и и 
| Для того, чтобы три вектора  , ,  и и  были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю: были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю:
 .
Условие компланарности трех векторов также можно записать в виде: .
Условие компланарности трех векторов также можно записать в виде:  , где хотя бы одно из чисел , где хотя бы одно из чисел 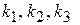 не равно нулю. не равно нулю.
| |||||
| АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ | ||||||
| МЕТОД КООРДИНАТ | Метод решения геометрических задач, в котором ведущую роль играют вычисления (действия с координатами), а построения имеют вспомогательное значение. | |||||
 -МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО -МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО 
|  -мерное линейное пространство, в котором определено скалярное произведение.
Обозначение: -мерное линейное пространство, в котором определено скалярное произведение.
Обозначение:  .
Например,
¨ координатная плоскость .
Например,
¨ координатная плоскость  с базисом с базисом  является двумерным эвклидовым пространством является двумерным эвклидовым пространством 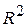 ;
¨ координатное пространство ;
¨ координатное пространство  с базисом с базисом 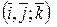 является трехмерным эвклидовым пространством является трехмерным эвклидовым пространством  . .
| |||||
ПОЛЯРНЫЕ КООРДИНАТЫ точки  на плоскости на плоскости
| Два числа, определяющие положение этой точки  относительно некоторой фиксированной точки относительно некоторой фиксированной точки 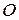 , называемой полюсом, и некоторого фиксированного луча , называемой полюсом, и некоторого фиксированного луча  , называемого полярной осью (см. рис). , называемого полярной осью (см. рис).
 Обозначение:
Обозначение:  , где первая координата , где первая координата  (полярный радиус) равна расстоянию от точки (полярный радиус) равна расстоянию от точки  до полюса ( до полюса (  ), а вторая координата ), а вторая координата  (полярный угол) - угол, образуемый отрезком (полярный угол) - угол, образуемый отрезком  с полярной осью с полярной осью  . .
| |||||
УРАВНЕНИЕ ЛИНИИ на плоскости (в пространстве 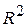 ) )
| Уравнение, связывающее координаты любой точки  («текущей точки»), лежащей на этой линии. Уравнение линии можно представить в виде равенства («текущей точки»), лежащей на этой линии. Уравнение линии можно представить в виде равенства
 ,
которому удовлетворяют координаты любой точки этой линии, и только они (т.е. координаты любой точки, не лежащей на данной линии, не удовлетворяют уравнению этой линии). ,
которому удовлетворяют координаты любой точки этой линии, и только они (т.е. координаты любой точки, не лежащей на данной линии, не удовлетворяют уравнению этой линии).
| |||||
| ПРЯМАЯ ЛИНИЯ на плоскости | Геометрическое место точек, координаты  которых удовлетворяют уравнению первой степени: которых удовлетворяют уравнению первой степени:
 (общее уравнение прямой на плоскости),
где хотя бы одно из чисел
(общее уравнение прямой на плоскости),
где хотя бы одно из чисел  и и  не равно нулю
( т.е. не равно нулю
( т.е. 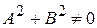 ).
Коэффициенты ).
Коэффициенты  и и  общего уравнения прямой являются координатами ее нормального вектора общего уравнения прямой являются координатами ее нормального вектора  , который перпендикулярен данной прямой.
Кроме общего уравнения, прямая на плоскости может быть задана и другими уравнениями, например: , который перпендикулярен данной прямой.
Кроме общего уравнения, прямая на плоскости может быть задана и другими уравнениями, например:
 ,
где ,
где  - угловой коэффициент прямой ( - угловой коэффициент прямой (  , ,  - угол, образуемый прямой с положительным направлением оси - угол, образуемый прямой с положительным направлением оси  ); );  - отрезок, отсекаемый прямой на оси - отрезок, отсекаемый прямой на оси  . .
| |||||
| УГОЛ МЕЖДУ ПРЯМЫМИ на плоскости | Тангенс угла между двумя прямыми:
 , ,
 определяется формулой
определяется формулой
 ,
которая дает угол ,
которая дает угол  , на который надо повернуть первую прямую, чтобы она стала параллельной второй прямой. , на который надо повернуть первую прямую, чтобы она стала параллельной второй прямой.
| |||||
| УСЛОВИЕ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПРЯМЫХ на плоскости | Условием параллельности двух прямых:
 , ,
 является равенство их угловых коэффициентов:
является равенство их угловых коэффициентов:
 ,
т.е. прямые параллельны, если их угловые коэффициенты равны, и не параллельны, если их угловые коэффициенты не равны. ,
т.е. прямые параллельны, если их угловые коэффициенты равны, и не параллельны, если их угловые коэффициенты не равны.
| |||||
| УСЛОВИЕ ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ПРЯМЫХ на плоскости | Условием перпендикулярности двух прямых:
 , ,
 является соотношение:
является соотношение:
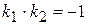 . .
| |||||
| РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ на плоскости | Длина перпендикуляра, опущенного из точки на прямую.
Расстояние  от точки от точки  до прямой до прямой
 определяется формулой
определяется формулой
 . .
| |||||
| ЛИНИЯ (КРИВАЯ) ВТОРОГО ПОРЯДКА на плоскости | Линия, которая определяется уравнением второй степени относительно текущих координат  : :
 ,
где хотя бы одно из чисел ,
где хотя бы одно из чисел  , ,  и и  не равно нулю.
При соответствующем выборе системы координат уравнение линии второго порядка можно привести к простейшему (каноническому) виду. не равно нулю.
При соответствующем выборе системы координат уравнение линии второго порядка можно привести к простейшему (каноническому) виду.
| |||||
| ОКРУЖНОСТЬ | Множество всех точек плоскости, находящихся на заданном расстоянии (радиус окружности) от данной точки (центра окружности). Если  - радиус окружности, а точка - радиус окружности, а точка  - ее центр, то уравнение окружности имеет вид: - ее центр, то уравнение окружности имеет вид:
 . .
| |||||
| ЭЛЛИПС | Множество всех точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (обозначаемая через  ), причем эта постоянная больше расстояния между фокусами (которое обозначают через ), причем эта постоянная больше расстояния между фокусами (которое обозначают через  ).
Если провести оси координат так, что ось ).
Если провести оси координат так, что ось  проходит через фокусы ( проходит через фокусы (  и и  ) эллипса, а ось ) эллипса, а ось 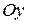 - посередине между фокусами и перпендикулярно оси - посередине между фокусами и перпендикулярно оси  (см. рис), то уравнение эллипса можно записать в простейшем (каноническом) виде: (см. рис), то уравнение эллипса можно записать в простейшем (каноническом) виде:

 , ,
где | |||||
| ГИПЕРБОЛА | Множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (обозначаемая через  ), причем эта постоянная меньше расстояния между фокусами (которое обозначают через ), причем эта постоянная меньше расстояния между фокусами (которое обозначают через  ).
Если провести оси координат так, что ось ).
Если провести оси координат так, что ось  проходит через фокусы ( проходит через фокусы (  и и  ) гиперболы, а ось ) гиперболы, а ось 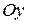 - посередине между фокусами и перпендикулярно оси - посередине между фокусами и перпендикулярно оси  (см. рис.), то уравнение гиперболы можно записать в простейшем (каноническом) виде: (см. рис.), то уравнение гиперболы можно записать в простейшем (каноническом) виде:
 , ,

 - действительная полуось гиперболы, - действительная полуось гиперболы,  - мнимая полуось гиперболы, причем - мнимая полуось гиперболы, причем  , ,  и и 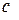 связаны соотношением связаны соотношением  . Координаты фокусов гиперболы в этом случае имеют вид: . Координаты фокусов гиперболы в этом случае имеют вид:  и и  . .
(Пунктирные прямые на рис. – асимптоты гиперболы). | |||||
| ПАРАБОЛА | Множество всех точек плоскости, равноудаленных от данной точки, называемой фокусом параболы, и данной прямой, называемой директрисой параболы.
Если директрисой параболы является прямая  , а фокусом – точка , а фокусом – точка  , то уравнение параболы имеет вид , то уравнение параболы имеет вид  . Эта парабола расположена симметрично оси . Эта парабола расположена симметрично оси  (см. рис). (см. рис).
 Уравнение
Уравнение 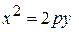 является уравнением параболы, расположенной симметрично оси является уравнением параболы, расположенной симметрично оси 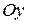 . .
| |||||
| АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ | ||||||
| ПЛОСКОСТЬ в пространстве | Геометрическое место точек пространства, координаты  которых удовлетворяют уравнению первой степени: которых удовлетворяют уравнению первой степени:
 (общее уравнение плоскости),
где хотя бы одно из чисел
(общее уравнение плоскости),
где хотя бы одно из чисел  , ,  и и  не равно нулю (т.е. не равно нулю (т.е.  ).
Коэффициенты ).
Коэффициенты  , ,  и и  общего уравнения плоскости являются координатами ее нормального вектора общего уравнения плоскости являются координатами ее нормального вектора  , который перпендикулярен данной плоскости. , который перпендикулярен данной плоскости.
| |||||
| УГОЛ МЕЖДУ ПЛОСКОСТЯМИ | Две плоскости
 , ,
 образуют четыре попарно равных двугранных угла. Один из них равен углу
образуют четыре попарно равных двугранных угла. Один из них равен углу  между нормальными векторами между нормальными векторами 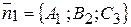 и и  и определяется формулой и определяется формулой
 Угол
Угол  , смежный с углом , смежный с углом  , определяется формулой , определяется формулой
 . .
| |||||
| УСЛОВИЕ ПАРАЛЛЕЛЬНОСТИ ПЛОСКОСТЕЙ | Если две плоскости
 , ,
 параллельны, то их нормальные векторы
параллельны, то их нормальные векторы 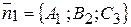 и и  коллинеарны (и обратно). Поэтому условие параллельности (необходимое и достаточное) имеет вид: коллинеарны (и обратно). Поэтому условие параллельности (необходимое и достаточное) имеет вид:
 . .
| |||||
| УСЛОВИЕ ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ | Если две плоскости
 , ,
 перпендикулярны, то их нормальные векторы
перпендикулярны, то их нормальные векторы 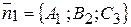 и и  перпендикулярны. Поэтому условие перпендикулярности имеет вид: перпендикулярны. Поэтому условие перпендикулярности имеет вид:
 . .
| |||||
| РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ | Длина перпендикуляра, опущенного из точки на плоскость.
Расстояние  от точки от точки  до прямой до прямой
 определяется формулой
определяется формулой
 . .
| |||||
| ПРЯМАЯ в пространстве | Всякая прямая линия в пространстве определяется системой двух уравнений первой степени
 (где коэффициенты
(где коэффициенты  не пропорциональны коэффициентам не пропорциональны коэффициентам  ),
представляющих две различные плоскости, проходящие через данную прямую (т.е. пересекающиеся по данной прямой).
Прямую можно определить и другими уравнениями.
Например, канонические уравнения прямой, проходящей через точку ),
представляющих две различные плоскости, проходящие через данную прямую (т.е. пересекающиеся по данной прямой).
Прямую можно определить и другими уравнениями.
Например, канонические уравнения прямой, проходящей через точку  , имеют вид: , имеют вид:
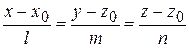 ,
где ,
где  , ,  и и  являются координатами направляющего вектора являются координатами направляющего вектора  , который параллелен данной прямой (или лежит на ней). , который параллелен данной прямой (или лежит на ней).
| |||||
| УГОЛ МЕЖДУ ПРЯМЫМИ в пространстве | Две прямые
 , ,
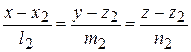 образуют четыре попарно равных угла. Один из них равен углу
образуют четыре попарно равных угла. Один из них равен углу  между направляющими векторами между направляющими векторами 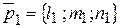 и и  и определяется формулой и определяется формулой
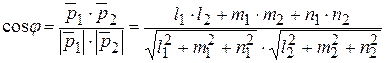 Угол
Угол  , смежный с углом , смежный с углом  , определяется формулой , определяется формулой
 . .
| |||||
| УСЛОВИЕ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ в пространстве | Если две прямые
 , ,
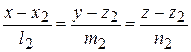 параллельны, то их направляющие векторы
параллельны, то их направляющие векторы 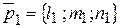 и и  коллинеарны. Поэтому условие параллельности имеет вид: коллинеарны. Поэтому условие параллельности имеет вид:
 . .
| |||||
| УСЛОВИЕ ПАРПЕНДИКУЛЯРНОСТИ ПРЯМЫХ в пространстве | Если две прямые
 , ,
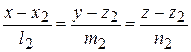 перпендикулярны, то их направляющие векторы
перпендикулярны, то их направляющие векторы 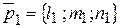 и и  перпендикулярны. Поэтому условие перпендикулярности имеет вид: перпендикулярны. Поэтому условие перпендикулярности имеет вид:
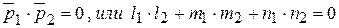 . .
| |||||
| УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ | Угол между прямой и ее проекцией на плоскость.
Угол между прямой
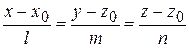 и
плоскостью и
плоскостью
 определяется по формуле
определяется по формуле
 ; ;
| |||||
| УСЛОВИЕ ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ | Условие параллельности прямой
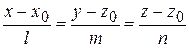 и
плоскости и
плоскости
 имеет вид:
имеет вид:
 .
Это условие выражает перпендикулярность направляющего вектора .
Это условие выражает перпендикулярность направляющего вектора  и нормального вектора и нормального вектора  . .
| |||||
| УСЛОВИЕ ПЕРПЕНДИКУЛЯРНОСТИПРЯМОЙ И ПЛОСКОСТИ | Условие перпендикулярности прямой
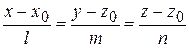 и
плоскости и
плоскости
 имеет вид:
имеет вид:
 .
Это условие выражает коллинеарность направляющего вектора .
Это условие выражает коллинеарность направляющего вектора  и нормального вектора и нормального вектора  . .
| |||||
| УРАВНЕНИЕ ПОВЕРХНОСТИ | Уравнение, связывающее координаты любой точки  («текущей точки»), лежащей на этой поверхности. Уравнение поверхности можно представить в виде равенства («текущей точки»), лежащей на этой поверхности. Уравнение поверхности можно представить в виде равенства
 ,
которому удовлетворяют координаты любой точки этой поверхности, и только они (т.е. координаты любой точки, не лежащей на данной поверхности, не удовлетворяют уравнению этой поверхности). ,
которому удовлетворяют координаты любой точки этой поверхности, и только они (т.е. координаты любой точки, не лежащей на данной поверхности, не удовлетворяют уравнению этой поверхности).
| |||||
| ПОВЕРХНОСТЬ ВТОРОГО ПОРЯДКА | Поверхность, которая определяется уравнением второй степени относительно текущих координат  : :
 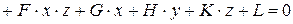 ,
где хотя бы одно из шести чисел ,
где хотя бы одно из шести чисел  , ,  , ,  , ,  , ,  , ,  не равно нулю. не равно нулю.
| < |
 ;
; ,
,
 .
. ;
; ,
, 
 . Координаты фокусов эллипса в этом случае имеют вид:
. Координаты фокусов эллипса в этом случае имеют вид: