 |
|
ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ
Термодинамика и молекулярная физика
● Основное уравнение кинетической теории идеального газа:

● Средняя энергия хаотического теплового движения молекул идеального газа:
 ,
,
где i – сумма поступательных, вращательных и удвоенного числа колебательных степеней свободы.
● Закон Дальтона для давления смеси газов:

● Наиболее вероятная, средняя и средняя квадратичная скорости молекул идеального газа:
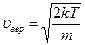 ,
, 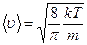 ,
, 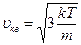 .
.
● Уравнение состояния идеального газа:
 ,
,
где М – молярная масса (масса моля).
● Первое начало термодинамики:
Q=ΔU+A,
где ΔU – приращение внутренней энергии системы.
● Внутренняя энергия идеального газа:
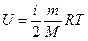 .
.
● Работа, совершаемая газом:
А = ∫ р dV.
● Работа, совершаемая газом при изотермическом изменении объема газа:
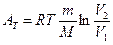 .
.
● Давление газа и его объем связаны при адиабатическом процессе уравнением Пуассона:
 ,
,
где γ – показатель адиабаты 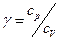 .
.
● Теплоемкость тела определяется как
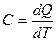 Дж/К,
Дж/К,
где Q количества тепла, сообщенное телу и повышающее его температуру на 1 К.
● Молярная теплоемкость, т.е. теплоемкость одного моля вещества
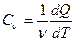 .
.
● Удельная теплоемкость
 .
.
● Теплоемкость при постоянном объеме:
 ,
,
где U – внутренняя энергия тела.
● Теплоемкость при постоянном давлении:
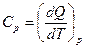 ,
,
● Молярная теплоемкость газа при политропическом процессе (рVn=const):
 .
.
● Внутренняя энергия идеального газа:
 .
.
● Уравнение состояния ван-дер-ваальсовского газа (для моля):
(p+ 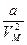 )(VM-b)=RT,
)(VM-b)=RT,
где VM – молярный объем, занимаемый при данных р и Т.
● Внутренняя энергия одного моля ван-дер-ваальсовского газа:
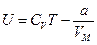 .
.
● Барометрическая формула:
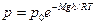 ,
,
где р0 – давление на высоте h=0.
● Распределение Максвелла молекул по скоростям:
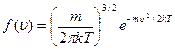 .
.
● Распределение Максвелла молекул по проекции скорости:
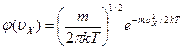 ,
,
.
● Распределение Максвелла по модулю скорости:

● Распределение Больцмана
 ,
,
где n – концентрация молекул, обладающих потенциальной энергией Wp, n0 - концентрация молекул, с нулевой потенциальной энергией.
● К.П.Д. тепловой машины:

где – Q1 – тепло, получаемое рабочим телом, Q2 – отдаваемое тепло.
● К.П.Д. цикла Карно:
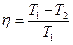 ,
,
где Т1 и Т2 – температуры нагревателя и холодильника.
● Неравенство Клаузиуса:
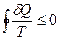 ,
,
где δQ – элементарное тепло, полученное системой (δQ – величина алгебраическая).
● Приращение энтропии системы:
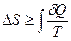 .
.
● Основное соотношение термодинамики:
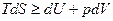 .
.
● Связь между энтропией и статистическим весом Ω (термодинамической вероятностью):
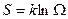 ,
,
где k – постоянная Больцмана.
● Соотношения между постоянными Ван-дер-Ваальса и параметрами критического состояния вещества:
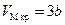 ,
, 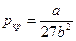 ,
, 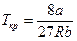 .
.
● Связь между критическими параметрами моля вещества:
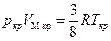 .
.
● Уравнение Клапейрона – Клаузиуса:
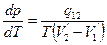 ,
,
где q12 – удельная теплота поглощаемая при переходе 1→2, V1’ и V2’ – удельные объемы фазы 1 и 2.
● Относительное число молекул газа, пролетающих путь s без столкновений:
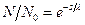 ,
,
где λ – средняя длина свободного пробега.
● Средняя длина свободного пробега молекулы газа:
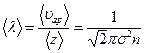 ,
,
где 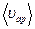 - средняя арифметическая скорость,
- средняя арифметическая скорость, 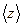 - среднее число столкновений каждой молекулы с остальными в единицу времени, σ – эффективный диаметр молекулы, n – концентрация молекул.
- среднее число столкновений каждой молекулы с остальными в единицу времени, σ – эффективный диаметр молекулы, n – концентрация молекул.
● Общее число столкновений всех молекул в единице объема за единицу времени:

● Масса, перенесенная за время Δt при диффузии,
 ,
,
где 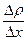 - относительное изменение плотности в направлении х, перпендикулярном к площадке ΔS.
- относительное изменение плотности в направлении х, перпендикулярном к площадке ΔS.
● Импульс, перенесенный газом за время Δt, определяет силу внутреннего трения Fтр в газе:
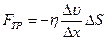 ,
,
где 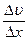 - относительное изменение скорости течения газа в направлении х, перпендикулярном к площадке ΔS.
- относительное изменение скорости течения газа в направлении х, перпендикулярном к площадке ΔS.
● Количество теплоты, перенесенное за время Δt вследствие теплопроводности, определяется формулой:
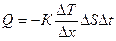
где 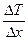 - относительное изменение температуры газа в направлении х, перпендикулярном к площадке ΔS.
- относительное изменение температуры газа в направлении х, перпендикулярном к площадке ΔS.
● Коэффициент диффузии D, вязкости η и теплопроводности א газов:
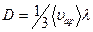 ,
, 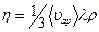 ,
, 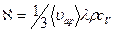 ,
,
где ρ – плотность газа, сV – его удельная теплоемкость при постоянном объеме.
● Сила трения, действующая на единицу поверхности пластин при их движении параллельно друг другу в ультраразреженном газе:
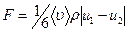 ,
,
где u1 и u2 скорости пластин.
● Плотность потока тепла, переносимого ультраразреженным газом между двумя стенками:
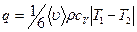 ,
,
где Т1 и Т2 – температуры стенок.
Твердые тела
● Изменение температуры плавления dТ при изменении давления на dр дается уравнением Клаузиуса-Клапейрона
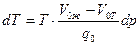 ,
,
где q0 – молярная теплота плавления, V0ж – молярный объем жидкости, V0Т - молярный объем твердого тела, Т – термодинамическая температура плавления.
● При не очень низких температурах для твердых тел имеет место закон Дюлонга и Пти, согласно которому молярная теплоемкость всех химически простых твердых тел равна приблизительно 3R = 25 Дж/(моль∙К).
● Количество теплоты Q, переносимое вследствие теплопроводности за время Δτ, определяется формулой:
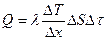 ,
,
где ΔТ/Δх – изменение температуры в направлении х, перпендикулярном к площадке ΔS, λ – теплопроводность.
● При повышении температуры длина твердых тел возрастает в первом приближении линейно с температурой:
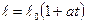 .
.
где ℓ - длина тела при температуре t, ℓ0 – его длина при температуре t0=0 оС, а – температурный коэффициент линейного расширения. Для твердых изотропных тел а=b/3, где b – температурный коэффициент объемного расширения.
Элементы кристаллографии
● Объем V0 одного килограмм-моля кристалла:
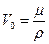 ,
,
где μ – киломоль, ρ – плотность кристалла.
● Объем V элементарной ячейки кристалла:
а) при кубической сингонии:
V = а3;
б) при гексагональной сингонии:
 ,
,
где а и с – параметры ячейки.
● Число Z0 элементарных ячеек в одном килограмм-моле кристалла
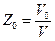
или
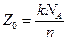 .
.
где k – число одинаковых атомов в химической формуле соединения, NА – число Авогадро, n – число одинаковых атомов, приходящихся на элементарную ячейку.
● Число Z0 элементарных ячеек в единице объема кристалла
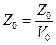 ,
,
а) в общем случае:
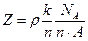 ;
;
б) для кристалла, состоящего из одинаковых атомов (k=1):
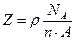 ,
,
где А – килограмм-атом.
● Параметр кубической решетки
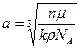 .
.
● Расстояние d между соседними атомами в кубической решетке:
а) в гранецентрированной:
 ;
;
б) в объемноцентрированной:
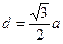 .
.
Тепловые свойства твердых тел.
● Энергия одного килограмм-атома химически простых (состоящих из одинаковых атомов) твердых тел в классической теории теплоемкости выражается формулой:
Е=3RТ,
где R – универсальная газовая постоянная, Т – абсолютная температура.
● Теплоемкость одного килограмм-атома химически простых твердых тел определяется по закону Дюлонга и Пти:
Сμ=3R.
● Для химически сложных тел (состоящих из различных аомов) теплоемкость одного киломоля определяется по закону Неймана-Коппа:
Сμ=n∙3R,
n – общее число частиц в химической формуле соединения.
● Среднее значение <ε> энергии квантового осциллятора, приходящееся на одну степень свободы, в квантовой теории Эйнштейна выражается формулой:
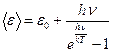 ,
,
где ε0 – нулевая энергия (ε0=0,5hν), h – постоянная Планка, ν – частота колебаний осциллятора, k – постоянная Больцмана, T – абсолютная температура.
● Энергия одного килограмм-атома кристалла в квантовой теории теплоемкости определяется как:
 ,
,
где 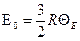 - нулевая энергия килограмм-атома,
- нулевая энергия килограмм-атома, 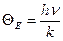 - характеристическая температура.
- характеристическая температура.
● Теплоемкость одного килограмм-атома кристалла в квантовом состоянии:
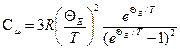 .
.
● Частотный спектр колебаний в теории Дебая задается функцией распределения частот g(ν). Число dZ собственных частот твердого тела, приходящихся на интервал частот от ν до ν+dν
dZ= g(ν)dν.
● Для трехмерного кристалла, содержащего N атомов:
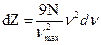 ,
,
νmax – максимальная частота, ограничивающая спектр колебаний.
● Энергия твердого тела:
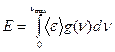 .
.
● Энергия одного килограмм-атома кристалла по Дебаю:
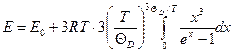 ,
,
где 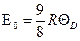 - нулевая энергия одного килограмм-атома кристалла по Дебаю,
- нулевая энергия одного килограмм-атома кристалла по Дебаю,  характеристическая температура Дебая.
характеристическая температура Дебая.
● Теплоемкость одного килограмм-атома кристалла по Дебаю:
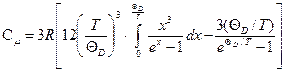 ,
,
● Энергия фонона связана с частотой ν колебаний:
ε=hν.
● Квазиимпульс фонона:
р=h/λ=ħk,
где λ – длина волны, ħ= h/2π, k=2π/λ – волновое число.
● Скорость фонона (групповая):
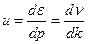 .
.
● Фазовая скорость фонона:
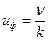 .
.
● Скорости волн в кристалле:
продольных – υℓ = 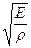 , поперечных – υt =
, поперечных – υt = 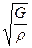 ,
,
где Е – модуль продольной упругости, G - модуль поперечной упругости, ρ – плотность твердого тела.
● Усредненное значение скорости звука определяется формулой:
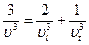 .
.
● Теплота перенесенная через поверхность площадью S, перпендикулярную направлению теплового потока за время dt, определяется законом Фурье:

א – коэффициент теплопроводности, dT/dx – проекция градиента температуры.
● Коэффициент теплопроводности א связан с удельной теплоемкостью (на единицу объема)  , скоростью звука υ и средней длиной свободного пробега фононов λ:
, скоростью звука υ и средней длиной свободного пробега фононов λ:
א =⅓  λυ
λυ
● Линейный коэффициент теплового расширения по определению:
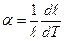 .
.
● Плотность тока насыщения при термоэлектронной эмиссии с катода дается формулой Ричардсона – Дэшмана:
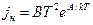 ,
,
где В=120(1-R) А/(см2К2), R - коэффициент отражения электронов проводимости от потенциального барьера на поверхности эмиттера, А – работа выхода электронов с поверхности катода.
Полупроводники.
● Удельная проводимость σ собственных проводников:
σ=n∙e(un+up),
где е – заряд электрона, n – концентрация носителей тока, un и up - подвижность электронов и дырок.
● Напряжение UX на гранях образца при эффекте Холла:
UX=RXBbj,
где RX - постоянная Холла, В – индукция магнитного поля, b – ширина пластины, j – плотность тока.
● Постоянная Холла для полупроводников типа алмаз, кремний, германий и др., обладающих носителями тока одного вида
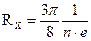 .
.