Главная | Обратная связь

Примеры выполнения типового расчета

1. Исследовать сходимость и найти сумму числового ряда:
.
Решение. Исследуем сходимость ряда:
~ .
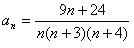Ряд с общим членом b_n сходится как обобщенный гармонический ряд при p = 2 > 1, следовательно, ряд с общим членом a_n сходится по признаку сравнения, связанному с пределом.
Преобразуем a_n в сумму простейших дробей методом неопределённых коэффициентов:
.
Приведем дроби в правой части равенства к общему знаменателю и приравняем числители полученных дробей, так как знаменатели у них одинаковые:
9n + 24 = A(n + 3)(n + 4) + Bn(n + 4) + Cn(n + 3).
Полученное равенство должно выполнять тождественно, т.е. оно должно быть справедливо не только для любого натурального n, но и для любого действительного переменного. Подставив в это равенство корни знаменателя исходной дроби, получим значения коэффициентов А, В, С :
n = 0 ­ ­ ­ ­ => ­ ­ 24 = 12A ­ ­ => ­ ­ A = 2;
n = –3 ­ ­ => ­ ­ –3 = –3B ­ ­ => ­ ­ B = 1;
n = –4 ­ ­ => ­ ­ –12 = 4C ­ ­ => ­ ­ C = –3.
Таким образом .
Запишем частичную сумму ряда:


.
Нетрудно заметить, что дроби со знаменателями 5; 6; 7; ... ; n взаимно сокращаются. После сокращения в выражении S_n остаются только дроби со знаменателями меньше 5 и больше n :

.
Сумма ряда S в этом случае равна:
.
Ответ: ряд сходится, его сумма равна .
2. С точностью ε = 10 ^–4 вычислить два интеграла. Для этого разложить подынтегральную функцию в степенной ряд, найти область его сходимости. Затем проинтегрировать его почленно и вычислить сумму полученного ряда с заданной точностью.

Решение 2.1. Воспользуемся разложением функции sin x в степенной ряд (1.7) и умножим этот ряд на , получим:

.

(1.8)

.
Для нахождения области сходимости исследуем полученный ряд на абсолютную сходимость по признаку Даламбера.


Рассматриваемый предел равен нулю, т.е. меньше единицы для любых х. Следовательно, полученный ряд сходится абсолютно при любом х.
Проинтегрируем обе части равенства (1.8) на отрезке [0; 1,5]:


.
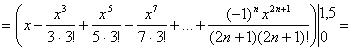
Воспользуемся правилом оценки погрешности знакочередующегося ряда по признаку Лейбница. При n = 2: ­ ­|a₂| ≈ 0,0127 > ε, при n = 3: |a₃| ≈ 0,00048 < ε. При вычислении остановимся на слагаемом a₂:
.
Ответ: 1,325; ­ ­ n = 2.
Решение 2.2. Разложим подынтегральную функцию e ^{– x} в степенной ряд по степеням х. Для этого в формуле разложения функции e ^x в степенной ряд (1.6) заменим х на –x² :
.
Полученный ряд сходится при любом х (проверьте самостоятельно). Следовательно, его можно почленно интегрировать на любом отрезке и, в частности, на отрезке [0;1]:


.
Получен знакочередующийся ряд, сходящийся по признаку Лейбница. Используем правило оценки погрешности для знакочередующегося ряда. При , при . Следовательно, для получения заданной точности можно при расчете остановиться на слагаемом a₄:
.
Ответ: 0,7475; ­ ­ n = 4.

Оформление отчета

В отчете необходимо привести все проделанные выкладки.
По первой задаче назвать признаки сходимости, использованные при его исследовании. В ответе записать сумму ряда в десятичных дробях.
По второй и третьей задачам найти область сходимости рядов, полученных при разложении подынтегральной функции, обосновать точность полученного при расчете результата. В ответе записать значение интеграла в десятичных дробях с четырьмя знаками после запятой и значение n при расчете частичной суммы ряда.