Главная | Обратная связь

Достаточные признаки сходимости

Теорема 13.5. (Признак сравнения). Пусть даны два ряда с неотрицательными членами (13.1.6) и (13.1.7) и для любого п выполняется неравенство

 

u_n ≤ v_n. (13.1.8)

Тогда

а) Из сходимости ряда (13.1.7) следует сходимость ряда (13.1.6),

б) Из расходимости ряда (13.1.6) следует расходимость ряда (13.1.7).

Схематическая запись признака сравнения

сх ← сх

расх → расх

 

Замечание. На практике признак сравнения наиболее удобно применять в следующем виде: если предел отношения u_n к v_n существует, конечен и не равен нулю, т.е.

 

, (13.1.9)

 

Где А = const, то ряды (13.1.6) и (13.1.7) сходятся или расходятся одновременно.

Если выполняется условие , то ряд называется мажорантой ряда (или мажорирующим рядом), а ряд - мажорируемым.

Для того, чтобы с помощью признака сравнения исследовать на сходимость ряды целесообразно знать ряды, сходимость или расходимость которых уже известна:

1) (ряд Дирихле) –

2) (гармонический ряд) – расходится.

3) –

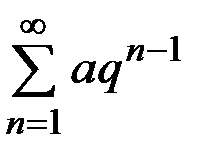Для того, чтобы найти ряд, с которым удобно проводить сравнения, полезно знать следующие неравенства

, , , ln x < x.

 

Существуют признаки сходимости, позволяющие судить о сходимости ряда, не сравнивая его с другим рядом.

Теорема 13.6. (Признак Даламбера) Пусть дан ряд (13.1.1) с положительными членами и существует предел

 

Тогда

а) при q < 1 ряд сходится;

б) при q > 1 ряд расходится;

в) при q = 1 о сходимости ряда ничего нельзя сказать (признак не работает), надо исследовать его, используя другие признаки.

Доказательство. Пусть По определению предела для любого как угодно малого e > 0 существует такое число N что для любого n ≥ N выполняется неравенство Отсюда следует, что

 

. (13.1.10)

 

а) Пусть q < 1. Докажем, что ряд (13.1.1) сходится.

Так как q > 1, то e можно взять настолько малым, что q + e < 1. Пологая

q + e = p рассмотрим правую часть неравенства (13.1.10)

 

или u_n+1 < pu_n для n = N, N + 1, ¼

 

Придавая п эти значения, из последнего неравенства получаем

 

u_N+1 < pu_N,

u_N+2 < pu_N+1 < p²u_N,

u_N+3 < pu_N+2 < p³u_N,

¼¼¼¼¼¼¼¼

т. е. члены ряда u_N+1+ u_N+2+ u_N+3+¼ меньше соответствующих членов ряда

 

p u_N + p²u_N + p³u_N + ¼ (13.1.11)

 

составленного из элементов геометрической прогрессии, причем убывающей, т. к. знаменатель ряда р < 1. Отсюда следует, что ряд (13.1.11) сходится. Тогда согласно признаку сравнения ряд

 

(13.1.12)

 

также сходится. Но ряд (13.1.12) получен из ряда (13.1.1) в результате отбрасывания конечного числа первых N членов, следовательно, по теореме 13.1 ряд (13.1.1) сходится.

б) Пусть теперь q > 1. Докажем, что ряд (13.1.1) расходится.

Возьмем e настолько малым, чтобы q – e > 1. Тогда при n ³ N в силу левой части неравенства (13.1.10) выполняется неравенство

 

или u_n+1>u_n.

Таким образом, члены ряда, начиная с некоторого номера N, возрастают с увеличением их номеров, т. е. общий член 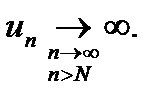Следовательно, согласно теореме 13.4 (необходимый признак сходимости ряда) ряд (13.1.1) расходится.

в) При q=1 ряд может, как сходится, так и расходится. В этом случае необходимо дополнительное исследование ряда с помощью других признаков. Теорема доказана.

 

Теорема 13.7. (Радикальный признак Коши) Пусть дан ряд (13.1.1) с положительными членами и существует предел

 

, (13.1.13)

 

то:

а) при q < 1 ряд сходится;

б) при q > 1 ряд расходится;

в) при q = 1 о сходимости ряда ничего нельзя сказать (признак не работает), надо исследовать его, используя друге признаки.

Доказательство проводится аналогично доказательству теоремы 13.6.

Теорема 13.8. (Интегральный признак сходимости Коши) Пусть для некоторого ряда (13.1.1) с положительными членами существует вещественная непрерывная функция f(x), определенная на [1, ¥), монотонно убывающая и такая, что f(n) = u_n для целых значений х = п. Тогда ряд (13.1.1) сходится тогда и только тогда, когда сходится (существует)несобственный интеграл

 

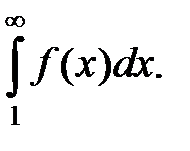
Если этот интеграл расходится (не существует), то расходится и ряд (13.1.1).

Исследуем, используя интегральный признак, на сходимость ряд

Дирихле ( обобщённый гармонический ряд)

.

Заменим п на х и тогда

При р = 1:

Þ при р > 1 данный интеграл сходится, а при р ≤ 1 - расходится. Следовательно, ряд сходится при р > 1 и расходится при р ≤ 1.

Замечание.Знакоположительными называются ряды с неотрицательными членами. Если все члены ряда – это неположительные числа, то умножая их на ( - 1 ) мы опять получим ряд с положительными членами. Поэтому все теоремы применимы ко всем знакопостоянным рядам.