Главная | Обратная связь

Остаток ряда и его оценка.

 

Определение. Ряд с произвольным распределением знаков его членов называется знакопеременным (т. е. ряд с произвольным расположением положительных и отрицательных членов).

Пусть дан знакопеременный ряд

 

(13.1.15)

 

Одновременно рассмотрим ряд, составленный из абсолютных величин членов знакопеременного ряда

 

. (13.1.16)

 

Для знакопеременных рядов имеет место следующий достаточный признак сходимости.

Теорема 13.10. (Достаточный признак сходимости знакопеременного ряда). Если ряд (13.1.16) сходится, то сходится и ряд (13.1.15).

Рассмотренный признак является достаточным, но не является необходимым, т. к. существуют знакопеременные ряды, которые сходятся, а ряды, состоящие из абсолютных величин их членов расходятся.

Например, ряд 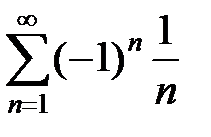сходится по признаку Лейбница, а гармонический ряд расходится. Поэтому все сходящиеся знакопеременные ряды можно разделить на абсолютно и условно сходящиеся.

Определение. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов.

Определение. Знакопеременный ряд называется условно сходящимся, если он сходится (например, по признаку Лейбница), а ряд, состоящий из абсолютных величин его членов, расходится.

Замечание. Знакочередующийся ряд является частным случаем

знакопеременного ряда.

После того как мы убедились в сходимости ряда, возникает вопрос о вычислении его суммы. Эта задача более сложная, т. к. сумму ряда во многих случаях вычислить невозможно. Поэтому чаще всего вычисляют приближенное значение суммы ряда с желаемой степенью точности.

Определение. Пусть дан ряд (13.1.15). Величина R_n=u_n+1+u_n+2+¼ называется остаточным членом ряда

Теорема 13.11. Если ряд (13.1.15) сходится, то его остаточный член стремится к нулю, когда п →∞.

Доказательство. Действительно, пусть ряд (13.1.15) сходится и S_n-его частичная сумма.

Сумма самого ряда равна

 

S=u₁+u₂+u₃+¼+u_n+¼=S_n+u_n+1+u_n+2+¼=S_n+R_n

 

или или R_n=S-S_n.

Учитывая, что , то . Теорема доказана.

В данной теореме утверждается следующее: если вместо точного значения S суммы ряда взять сумму S_n его первых п членов, то ошибка будет равна R_n, а т. к. R_n®0 при п®∞, следует, что всегда можно взять п настолько большим, чтобы R_n было сколь угодно малым.

Другими словами, сумму сходящегося ряда всегда можно вычислить с любой точностью, а величина R_n укажет ошибку при замене суммы ряда суммой его первых п членов. Для приближенных вычислений при помощи рядов оценка этой ошибки весьма существенна. Особенно просто удается оценить погрешность в случае знакочередующегося ряда.

Теорема 13.12. Для знакочередующегося ряда, удовлетворяющего условиям признака Лейбница, остаток его R_n по абсолютной величине меньше абсолютного значения первого из отброшенных членов |R_n|<u_n+1, причем знак остатка совпадает со знаком своего первого члена u_n+1.

 

 

Схема