|
|
Методичні вказівки.
Пряма лінія на площині.
Розрахункові завдання.
Задача1. В задачах 1.1-1.30 задані координати вершин трикутника АВС. Знайти:
1)довжини сторін АВ,ВС, та АС;
2)рівняння сторін АВ, АС, ВС;
3)кутові коефіцієнти сторін АВ, АС та ВС;
4)величину кута В в радіанах з точністю до двох знаків;
5)довжину бісектриси ВF внутрішнього кута В;
6)рівняння висоти АЕ та її довжину;
7)рівняння медіани СD та координати точки Р перетину цієї медіани з висотою АЕ;
8) рівняння середньої лінії KN трикутника;
9)площу трикутника;
10)побудувати на міліметровому папері (формат А4) трикутник АВС та знайдені його елементи в системі координат ХОУ, взявши за 1 масштабну 1 см.
1.1 А(-5;4) В(5;8-β) С(1;1)
1.2 А(-6;-2) В(-3;-11- β) С(-1;-5)
1.3 А(-3;1) В(1;5- β) С(2;5)
1.4 А(-4;6) В(-7;-6- β) С(-3;-5)
1.5 А(-8;-3) В(12;-2- β) С(-8;-2)
1.6 А(-7;4) В(6;-3- β) С(-4;1)
1.7 А(-2;3) В(-2;-1- β) С(5;-8)
1.8 А(-6;5) В(5;-9- β) С(-1;0)
1.9 А(-5;4) В(0;-4- β) С(6;-6)
1.10 А(-8;-3) В(-4;10- β) С(-5;7)
1.11 А(-7;7) В(4;-3- β) С(-7;2)
1.12 А(-4;1) В(8;-8- β) С(-3;2)
1.13 А(-6;3) В(-1;3- β) С(0;-3)
1.14 А(5;-1) В(-13;-5- β) С(-6;-1)
1.15 А(-5;9) В(-3;9- β) С(0;-6)
1.16 А(-8;4) В(7;11- β) С(-6;-7)
1.17 А(-9;7) В(-11;-4- β) С(1;-5)
1.18 А(-3;2) В(1;-1- β) С(-5;4)
1.19 А(-1;5) В(-8;-1- β) С(-1;9)
1.20 А(-8;3) В(-2;-6- β) С(-5;7)
1.21 А(-4;2) В(4;7- β) С(-6;9)
1.22 А(-5;0) В(-4;-9- β) С(9;5)
1.23 А(-7;5) В(1;1- β) С(0;1)
1.24 А(4;0) В(-1;-2- β) С(-3;8)
1.25 А(-8;3) В(3;-3- β) С(-8;2)
1.26 А(-2;5) В(-3;-5- β) С(11;-5)
1.27 А(-4;10) В(0;-9- β) С(-4;7)
1.28 А(-6;0) В(2;-6- β) С(2;-9)
1.29 А(-4;5) В(-2;-3- β) С(-6;-10)
1.30 А(-3;0) В(8;-8- β) С(-2;-3)
Методичні вказівки
Розв’язання задачі. Задані координати вершин трикутника А(-2,3), В(4,-2-β), С(3,7).
Візьмемо β=4, тоді координати вершин трикутника будуть такі:
А(-2,3),В(4,-6),С(3,7).
1.Відстань d між точками А(х  ,у
,у  ) та В(х
) та В(х  ,у
,у  ) визначається за формулою
) визначається за формулою
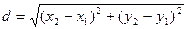 (1)
(1)
Використовуючи (1), знаходимо довжину сторони АВ:
d=  (лін. од.)
(лін. од.)
Аналогічно знаходимо довжини сторін ВС та АС:
d= 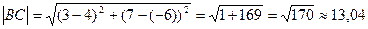 (лін. од.)
(лін. од.)
d=  (лін. од.).
(лін. од.).
2. Рівняння прямої, яка проходить через точки А(х  ,у
,у  ) та В(х
) та В(х  ,у
,у  ) має вигляд:
) має вигляд:
 . (2)
. (2)
Підставляючи в (2) координати точок А та В, одержимо рівняння сторони АВ:


6(у-3)=-9(х+2) \:3
2(у-3)=-3(х+2)
2у-6=-3х-6
3х+2у=0 (АВ).
Підставляючи в (2) координати точок А та С, дістанемо рівняння сторони АС:

5(у-3)=4(х+2)
4х-5у+23=0 (АС).
Аналогічно знаходимо рівняння сторони ВС:

-1(у+6)=13(х-4)
13х+у-46=0 (ВС).
3.Розв’язавши кожне з рівнянь сторін (АВ), (АС) та (ВС) відносно у, знаходимо їх рівняння у вигляді рівнянь прямих з кутовим коефіцієнтом:
(АВ) 2у=-3х; у=  , звідки
, звідки 
(АС) 5у=23+4х; у= 
(ВС) у=-13х+46; к=-13.
4.Відомо, що тангенс кута φ між двома прямими, кутові коефіцієнти яких відповідно дорівнюють к  та к
та к  , обчислюються за формулою:
, обчислюються за формулою:
Tgφ=  (3)
(3)
Знайдемо кут В, утворений прямими АВ та ВС, кутові коефіцієнти яких знайдені:
к  =к
=к  =-13; к
=-13; к  =к
=к  .
.
Використовуючи формулу (3), дістанемо:
tg B=  ,
,
Тоді в радіанах з точністю до двох знаків кут В дорівнює
5.Довжину бісектриси BF знаходимо як відстань між двома точками B та F. Невідомі координати х,у точки F визначаємо за формулами:
х=  у=
у= 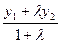 , де відношення λ=
, де відношення λ=  і координати точок А та С-відомі: А(х
і координати точок А та С-відомі: А(х  ,у
,у  ) та С(х
) та С(х  ,у
,у  )
)
Використовуючи властивість бісектриси внутрішнього кута трикутника, дістанемо:

Так як точка F ділить відрізок АС у відношенні λ=0,69, то згідно з (4) знаходимо:
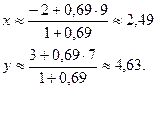
Отже, точка F(2,49;4,63).
Для знаходження довжини бісектриси BF використаємо формулу (1):
 (лін. од).
(лін. од).
Отже, d  =10,7 .
=10,7 .
6. Рівняння прямої, що проходить через дану точку 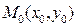 в заданому напрямку к, має вигляд:
в заданому напрямку к, має вигляд:
у-у  =к(х-х
=к(х-х  ) (5)
) (5)
Висота АЕ перпендикулярна до сторони ВС. Для того. Щоб знайти кутовий коефіцієнт висоти АЕ будемо використовувати умову перпендикулярності прямих
 або
або 
Так як к  =-13 , то
=-13 , то 
 . Підставляючи в (5) замість х
. Підставляючи в (5) замість х 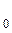 , у
, у 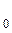 координати точки А: х
координати точки А: х  =-2, у
=-2, у  =3 та знайдений кутовий коефіцієнт висоти к=к
=3 та знайдений кутовий коефіцієнт висоти к=к  =
= 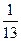 , дістанемо:
, дістанемо:
у-3= 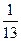 (х+2);
(х+2);
х-13у+41=0 (АЕ).
Для того, щоб знайти довжину висоти АЕ, визначимо координати точки Е-точки перетину прямих ВС та АЕ, розв’язавши систему рівнянь.

 (ВС) 13х+2у=0 х=
(ВС) 13х+2у=0 х= 
 у=3,2
у=3,2
(АЕ) х-13у+41=0 у= 
 -13у+41=0 х=-0,5
-13у+41=0 х=-0,5
Таким чином, Е(-0,5;3,2).
За формулою (1) знаходимо довжину висоти АЕ:
 (лін. од.)
(лін. од.)
7. Для того щоб знайти рівняння медіани СD, визначимо спочатку координати точки D, середини сторони АВ. Для цього використаємо формули ділення відрізка на дві рівні частини (дивись (4), де λ=1):

Отже, точка D(1;-1,5).
Підставляючи в (2) координати точок С та D, знаходимо рівняння медіани:
 . Після деяких перетворень отримуємо рівняння медіани CD:
. Після деяких перетворень отримуємо рівняння медіани CD:
8,5х-2у-11,5=0 (CD).
Для того, щоб знайти координати точки Р перетину висоти АЕ та медіани CD, розв’яжемо систему рівнянь:



 (АЕ) х-13у+41-0 х-13у+41=0 х=13у-41 у=3,3
(АЕ) х-13у+41-0 х-13у+41=0 х=13у-41 у=3,3

(CD) 8,5х-2у-11,5=0 ( 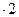 ) 17х-4у-23=0 17(13у-41)-4у-23=0 х=1,9
) 17х-4у-23=0 17(13у-41)-4у-23=0 х=1,9
Таким чином, точка Р(1,9;3,3).
8.Для знаходження середньої лінії KN, спочатку знайдемо точку К як середину відрізка АВ, знаючи координати точок А і В.
 ,
,
Отже, точка К(1;-1,5).
Аналогічно знаходимо координати точки N:

N (3, 5; 0, 5).
Тепер запишемо рівняння середньої лінії:

Спростивши це рівняння, отримуємо рівняння KN:
2x-2, 5y+1, 75=0 (KN).
9.Знайдемо площу трикутника за формулою (8), знаючи координати його вершин:




 х
х  у
у  1
1
 х
х  у
у  1
1
х  у
у  1
1
 |  |  |  |
-2 3 1
 4 -6 1 =
4 -6 1 =  (кв.од.)
(кв.од.)
3 7 1
10.Трикутник АВС, бісектриса BF, висота CD, медіана AE, пряма KN побудовані в системі координат ХОУ на мал.1
Задача 3. В задачах 3.1-3.30 задані координати точок А,В,С. Потрібно:
1)записати канонічне рівняння прямої АВ;
2)записати рівняння площини W, яка проходить через точку С, перпендикулярно до прямої АВ;
3)знайти точку К перетину площини з прямою АВ;
4)записати рівняння прямої, яка проходить через точку В паралельно до площини W, як лінію перетину двох площин;
5)знайти точку L, яка симетрична для точки С відносно прямої АВ;
6)знайти відстань від точки С до прямої АВ.
3.1 А(4+β;4;7) В(1+ β;5- β;2+ β) С(4;6;2)
3.2 А(8- β;-4;1) В(3+ β;-2- β;6- β) С(2;-5;3)
3.3 А(1+ β;5;3) В(2+ β;3+ β;-2- β) С(-2;6;-1)
3.4 А(-1- β;-2;0) В(-1- β;7+ β;1- β) С(5;1;-1)
3.5 А(3+ β;9;-2) В(5+ β;- β;8- β) С(0;-5;5)
3.6 А(-2+ β;6;4) В(4- β;- β;3- β) С(2;-2;2)
3.7 А(β;4;-7) В(-1- β;4- β;1- β) С(4;-2;6)
3.8 А(5- β;1;-5) В(5- β;-1+ β;1+ β) С(3;2;-1)
3.9 А(5- β;3;-2) В(-5+ β;3+ β;3+ β) С(-2;7;-2)
3.10 А(-2- β;0;6) В(7+ β;-2- β;2+ β) С(7;-3;7)
3.11 А(β;-7;5) В(4- β;4+ β;-1+ β) С(3;-6;6)
3.12 А(1+ β;-2;1) В(-2+ β;-2+ β; β) С(1;-3;-5)
3.13 А(4+ β;8;-1) В(5- β;-2+ β;-5+ β) С(6;4;-2)
3.14 А(2+ β;3;1) В(3- β;-2- β;-4- β) С(4;-4;6)
3.15 А(7- β;-6;2) В(4+ β;2- β;5+ β) С(-1;1;-1)
3.16 А(5+ β;-1;-1) В(2+ β;-8- β;2+ β) С(6;-3;3)
3.17 А(8- β;-4;0) В(4- β;-5+ β;7- β) С(9;-3;6)
3.18 А(3+ β;-1;3) В(-4+ β;5- β;-3+ β) С(-2;1;4)
3.19 А(-7+ β;6;-2) В(-5- β;3- β;-3- β) С(7;4;2)
3.20 А(-2+ β;1;-4) В(3+ β;-4- β;3+ β) С(3;-4;3)
3.21 А(β;-1;-1) В(7- β;-7- β;4+ β) С(3;3;2)
3.22 А(5+ β;5;-1) В(-4+ β;8- β;-2+ β) С(10;2;-2)
3.23 А(3- β;-2;-1) В(5+ β;9- β;7+ β) С(5;-1;5)
3.24 А(-2- β;2;0) В(-1+ β;1- β;4+ β) С(1;-4;5)
3.25 А(-4- β;-4;8) В(-6+ β;6- β;3+ β) С(4;-4;9)
3.26 А(1+ β;-1;-2) В(8- β;7- β;8+ β) С(9;7;0)
3.27 А(6- β;-7;5) В(-2- β;4+ β;4- β) С(2;-5;2)
3.28 А(-2+ β;0;-4) В(5- β;-2- β;5+ β) С(0;5;-5)
3.29 А(8+ β;1;-5) В(9- β;3+ β;-3- β) С(-4;2;1)
3.30 А(-3+ β;-6;3) В(β;-4+ β;-8- β) С(5;-11;0)
Розв’язання задачі.
Дано координати точок А,В,С. А(5+b,1+b,3); В(9,3+b,3);
С(1,2,3).Візьмемо b=3, тоді координати точок А,В,С будуть такі: А(8,4,9); В(9,6,3); С(1,2,3).
1.Рівняння прямої в просторі, яка проходить через точки А( x1,y1,z1) та B(x2,y2,z2) мають вигляд
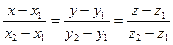 (1)
(1)
Підставляючи в (1) координати точок А та В, дістанемо

Тут ах ={1,2,-6} - направляючий вектор прямої АВ.
2. Запишемо рівняння площини W в загальному вигляді: Ax+By+Cz+D=0. (2)
Якщо площина проходить через точку Ко( xo,yo,zo), то її рівняння можна записати так
A(x-xo)+D(y-yo)+C(z-zo)=O,
де  - нормальнийвектор площини, який перпендикулярний до площини.
- нормальнийвектор площини, який перпендикулярний до площини.
Так як шукана площина W перпендикулярна до прямої АВ, то нормальний вектор  такої площини буде колінеарним направляючому вектору
такої площини буде колінеарним направляючому вектору 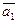 прямої АВ, а тому можна взяти взагалі
прямої АВ, а тому можна взяти взагалі  =
= 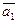 =
=  .
.
Замінемо коефіцієнти А,В,С в рівнянні (2) числами 1,2,-6 і підставимо замість xo,yo,zo координати точки С(1,2,3),дістанемо

x+2y-6z+13=0.
3.Визначимо координати точки К перетину площини W з прямою АВ. Для цього спочатку запишемо параметричні рівняння прямої АВ. Нехай

де t- деякий параметр, звідки
 ,тобто x=t+8, y=2t+4, z=-6t+9. (4)
,тобто x=t+8, y=2t+4, z=-6t+9. (4)
Підставляючи (4) в (3) знаходимо значення параметра t, при якому точка прямої АВ буде належати і площині W:
t+8+2(2t+4)-6(-6t+9)+13=0

Підставляючи в (4)  , знаходимо координати точки К перетину прямої
, знаходимо координати точки К перетину прямої
АВ з площиною W:



Отже точка К(8,6;5,2;5,3).
4.Канонічні рівняння прямої в просторі мають вигляд
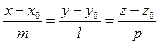 , (5)
, (5)
де (xo,yo,zo) - координати точки, через яку проходить пряма (5); m,l,p - координати направляючого вектора  цієї прямої
цієї прямої  =( m,І,р). За умовою пряма проходить через точку В(9,6,3) паралельно до площини W (3) з нормальним вектором
=( m,І,р). За умовою пряма проходить через точку В(9,6,3) паралельно до площини W (3) з нормальним вектором  . Скалярний добуток
. Скалярний добуток  , де
, де
а2 ={т2,і2,р2}, звідки



Візьмемо, наприклад l2 =1, p2 =-1, тоді m2 =-6-2=-8. Отже маємо а2= {-8,1,-1}.
Підставляючи в (5) замість xo,yo,zo координати точки В: xB=9,yB=6,zB=3 та замість m,І,р - числа -8,1,-1 і дістанемо канонічні рівняння шуканої прямої BD, паралельної до площини W:
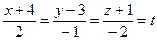 , де t- деякий параметр. Тоді рівняння прямої можна записати так:
, де t- деякий параметр. Тоді рівняння прямої можна записати так:

x + 4 = 2t; y - 3 = -t; z + l = -2t. (6)
х = 2t - 4; у = -t + 3; z = -2t - 1.
Підставляючи (6) в (2), знаходимо значення параметра t, при якому точка прямої (6) буде належати і площині W:
2(2t-4)-(-t+3)-2(-2t-1)-3=0
9t-12=0

4 Підставляючи в (6) значення  , знаходимо координати точки К
, знаходимо координати точки К
перетину прямої (4) з площиною W (2):
 (bd) (6)
(bd) (6)
Зрівнюючи попарно вирази в рівняннях (6), запишемо шукане рівняння прямої BD, як лінію двох площин p1, та p2:




 (BD) x - 8z + 15 = 0
(BD) x - 8z + 15 = 0
y – z – 3 = 0
5.Так як пряма АВ перпендикулярна до площини W, то люба пряма, яка розташована в цій площині, буде перпендикулярна до прямої АВ. Отже пряма СК перпендикулярна до прямої АВ, а тому шукана точка L, яка розташована симетрично до точки С, відносно прямої АВ, знаходиться на прямій СК. Пряма СК розташована в площині W, крім того точка К є середина відрізка CL. Застосовуючи формули для знаходження координат точки, яка ділить відрізок на дві рівні частини ( в просторі).
 (7)
(7)
Знаходимо координати шуканої точки L:






Отже знайдена точка L(16,2;8,4;7,6).
6. Для того, щоб знайти відстань від точки С до прямої АВ, достатньо обчислити відстань від точки С( 1,2,3) до точки перетину L(16,2;8,4;7,6). Дійсно, так як пряма АВ перпендикулярна до площини W, to шукана відстань дорівнює довжині перпендикуляра СК(СК^АВ). Отже, маємо:

(лін. одиниць).
Задача 4. В задачах 4.1-4.30 задані координати точок А,В,С та Р. Потрібно знайти:
1) рівняння площини W, яка проходить через три точки А,В,С;
2) канонічні рівняння прямої, яка проходить через точку Р, перпендикулярно до площини W; ,
3) точки К1, К2, К3, К4 перетину одержаної прямої з площиною W та з координатними площинами ХОУ, XOZ,YOZ;
4) відстань від точок Р та D до площини W;
5) координати точки М, яка симетрична точці Р відносно площини W.
4.1 A(y;-4+ y;6+ y) B(1+y;3-y;3-y) C(8-y;3+y;-2+y)
D(2+ y;-1 + y;4-y) P(6- y;6+ y;2- y)
4.2 A(3+y;-1+y;-1-y) B(6-y;3-y;3+y) C(9-y;-1-y;7-y)
D(-4+ y;4+ y;8-y) P(3+ y;2- y;5+ y)
4.3 A(5+y;-14+y;-3-y) B(2+y;1-y;1+y) C(6-y;2-y;2+ y)
D(5+ y;-14+ y;-3-y) P(10- y;4- y;7- y)
4.4 A(-10+y;-1-y;-2-y) B(2+y;1-y;1+y) C(6+y;2-y;2-y)
D(5+ y;-14+ y;-3-y) P(10- y;4- y;7- y)
4.5 A(-4+y;1-y;2+y) B(3+y;1-y;5+y) C(3+y;2+y;1-y)
D(4+ y;-10+ y;3-y) P(7- y;1- y;1+ y)
4.6 A(-2+y;3-y;y) B(2+ y;7- y;-5+ y) C(1-y;3+y;2-y)
D(8+ y;-12+ y;4-y) P(4-y;-1-y;8+ y)
4.7 A(-3+y;5-y;1+y) B(3+y;5-y;-1+y) C(5-Y;10+Y;12-y)
D(5+ y;-3+ y;1 -y) P(3- y;-3- y;-1+ y)
4.8 A(-7+y;13+ y;-1+ y) B(-3-y;-5-y;-11+y) C(-2-y;1+y;2-y)
D(-5+ y;-12+ y;-1-y) P(-1- y;-6- y;-11+ y)
4.9 A(-5+y;7-y;4+y) B(-2+y;-7-y;-2+y) C(-1-y;-3+y;12+y)
D(7+y;-1+y;6-y) P(11-y;-7-y;5+y)
4.10 A(-3+y;7+y;1+y) B(10+ y;2-y;-1+ y) C(12-y;1+y;1-y)
D(5+ y;-3+ y; 1 -y) P(3- y;-3- y;-1 + y)
4.11 A(-14+y;3-y;-7+y) B(-3-y;-4-y;-1+y) C(-9-y;1+y;-2-y)
D(-9+ y;-7+ y;-2-y) P(-5- y;-9- y;-16+ y)
4.12 A(-11+y;-1-y;8+y) B(-3+ y;1+ y;3+ y) C(-3+y;12+ y;6-y)
D(3+ y;-2+ y; 10-y) P(1 - y; 15- y; 11 + y)
4.13 A(-8+y;2-y;3y) B(8+ y;9- y;-5- y) C(-1-y;6+y;-2-y)
D(2+ y;-10+ y;3-y) P(-4- y;-i- y;8- y)
4.14 A(-1+y;9-y;-1+y) B(9+y;1-y;2+y) C(5-y;8+ y;2- y)
D(12+ у;-3+ y;4-y) P(1+ y;6- y;-4+ y)
4.15 A(-1+y;1-y;-7+y) B(-9+y;-3-y;-1+y) C(-3-y;-1+y;-2-y)
D(11+ y;-1+ y;-9-y) P(-2- y;-4- y;-1+ y)
4.16 A(-6+y;1-y;9+y) B(-12+y;-7+y;-8+y) С(-3-у;-4+ y;2- y)
D(7+y;-1-y;7-y) P(1-y;-5-y;-5-y)
4.17 A(-6+y;3+y;-1+y) B(1+y;4-y;-4+y) C(2-y;-1-y;1+y)
D(8+ y;-4+ y;7-y) P(1- y;-4- y;-6+ y)
4.18 A(-14+y;3-y;-7+ y) B(-3- y;-4- y;-1+ y) C(-9-y;1+ y;-2-y)
D(y;-2-y;10-y) P(10-y;1-y;1+y)
4.19 А(-8+y;19-у;-2+y) В(-1+у;1+у;3+y) С(5-у;2+у;10-у)
D(l +у;-2+y; 1-у) Р(-1+y;4-у;-14+у)
4.20 А(-9+;2- у ;-2+у) В(-4+y;-6-у;-2+y) С(-5-у;-2+у;-6-у)
D(1+y;-9+ y +;-3- y ) Р(-3-у;-11-y;-12+у)
4.21 А(3+y;5-у;-5+у) В(-2+y;-9+y:-5+у) С(-12+y;9+у;4+y)
D(5+y;-2+y;-9+y) Р(2+у;6+у;6+у)
4.22 А(-6+у;-1+у ;-1+у) В(4+у;7+у;6+у) С(7+у;14-у;8+y)
D(-2-y ;-2+у;3+у) Р( 1 +y;3-у;-8+у)
4.23 А(-6+у;у ;-2-у) В(7+y;-5-у;3-у) С(-3-у;9+у;8+у)
D(8-y;9-y;3+y) P(-l-y;4+y;10-y)
4.24 А(-1+y:6+у;6+y) В(15-у;3+y;9-у) С(5+у;у;-4+у)
D(3+y;4+y;7+y) P( 11 -у; 11 -у; 14+y)
4.25 А(-1+y;8-у;-9+y) В(4+y;-3-у;6+y) С(2+y;3+у;4+y)
D(7+y;5+y;-7+y) Р(-3+y;6+y;9+y)
4.26 А(-2+у;6+y;11+y) В(-7+у;7+y;5+у) С(-12+у;15-у;4+y)
D(-3-y;-5+y;6+y) Р(-4+у;3-у;3+y)
4.27 А(-12+y;3+y ;-3+у) B(-3+y;-19-у;-7+y) С(7+y;9+y;8+y)
D(l+y;4+y;-13+y) P(-l+y;-2+y;11+y)
4.28 А(7+y;13-у;-6+у) В(-5+у;7+у;4+у) С(6+у;8+у; 11+у)
D(l+y;-5+y;12+y) P(-4+y;14-y;-7+y)
4.29 А(-4+y;7+y;-2+у) В(-7+y;3-у;-2+y) С(6-у;-6+у;-6+у)
D(-2+y;5+y;-3-y) Р(-2-у;-4-у;-1+y)
4.30 А(6+у;5-у ;-5+у) В(-2+y;7+у;8+y) С(4+y;6+y;5+y)
D(-2+y;2+y;-4+y) Р(-3+y;-5+у;5+y)
Методичні вказівки.
Розв'язання задачі. Дано такі координати точок
А(4+y;6+y;-1+y) В(7+у;2+у;4+у) С(-2+y;у;-4+y)
D(-1+y;1+у;-3+y) Р(-5+у;2+y;-2+у). Нехай у=1, тоді координати точок будуть такі:
А(5;7;0), В(8;3;5), C(-l;l;-3), D(0, 2, -2), Р(-4, 3, -1).
1.Рівняння площини, яка проходить через три точки:
А( x1,y1,z1); В( х2,у2,z2); С( x3,y3,z3), має вигляд
 (1)
(1)
Підставивши в (1) координати точок А,В,С, дістанемо

Розкладемо визначник, який записано зліва, по елементам першого рядка
(x-5)14-(y-7)7-14z=0
14x-7y-2z-3=0
2x-y-2z-3=0. (W) (2)
де  - нормальний вектор площини.
- нормальний вектор площини.
2. Канонічне рівняння прямої в просторі мають вигляд
 ,
,
де 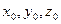 - координати точки через яку проходить пряма (3); m,l,p-координати направленного вектора
- координати точки через яку проходить пряма (3); m,l,p-координати направленного вектора  цієї прямої:
цієї прямої:  = {m,l,p}. За умовою пряма проходить через точку Р(-4,3,-1) та перпендикулярна до площини W. Отже підставляючи в (3) замість
= {m,l,p}. За умовою пряма проходить через точку Р(-4,3,-1) та перпендикулярна до площини W. Отже підставляючи в (3) замість 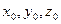 координати точки Р, та взявши вектор
координати точки Р, та взявши вектор  =
=  , тобто замість m,l,p в (3) підставляємо числа 2,-2,-2.
, тобто замість m,l,p в (3) підставляємо числа 2,-2,-2.

3. Для того, щоб знайти точки перетину прямої (4) з площиною (2), запишемо спочатку параметричні рівняння цієї прямої (4).
 , де t-деякий параметр. Тоді рівняння прямої можна записати так:
, де t-деякий параметр. Тоді рівняння прямої можна записати так:

x+4=2t; y-3=-t; z+1=-2t.
x=2t-4; y=-t+3; z=-2t-1.
Підставляючи в (5) значення 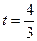 , знаходимо координати точки К перетину прямої (4) з площиною W(2):
, знаходимо координати точки К перетину прямої (4) з площиною W(2):



Одже К 
Нехай К1 - точка перетину прямої (4) з координатною площиною ХОУ; рівняння цієї площини z=0. При z=0, враховуючи (6), дістанемо:


Одже К1 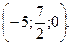
Нехай К2 - точка перетину прямої (4) з координатною площиною ХОУ; рівняння цієї площини у=0. При у=0, враховуючи (6), дістанемо:


Отже К2(2;0;-7).
Нехай К3-точка перетину прямої (4) з координатною площиною YOZ; Рівняння цієї площини х=0. При х=0, враховуючи (6), дістанемо:
0=2t3-4; t3=2.
y=-2+3=1;z3=-2*2-1=-5;x3=0.
 К3 =
К3 = 
4. Відстань від точки до площини - це є найкоротша відстань, тобто дорівнює довжині перпендикуляра, який проведений з цієї точки до площини.
Так як точка Р розташована на прямій (4), яка перпендикулярна до площини W , і перетинається з площиною в точці К, то для знаходження відстані від точки Р до площини W достатньо знайти відстань між точками Р та К:

Отже РК=4 (лін.од).
Відстань d від точки P(x,y,z) до площини, яка має загальне рівняння
Ax+By+Cz+D=0 можна обчислити за такою формулою:
 (7)
(7)
Підставляючи в формулу (7) замість х, у ,z- координати точки D={0,2,-2} та значення А=2, В=-1, С=-2, D=-3. Із загального рівняння (2) площини W, знайдемо шукану відстань d від точки D до площини W:
 (лін.од.)
(лін.од.)
 (лін.од.)
(лін.од.)
5. Так як пряма РК (4) перпендикулярна до площини W, то шукана точка М, яка розташована симетрично до точки Р, відносно площини W, знаходиться на прямій РК. Крім того, точка К є серединою відрізка РМ. Використовуючи формули для знаходження координат точки, яка ділить відрізок (в просторі) на дві рівні частини, знаходимо координати шуканої точки М:
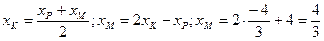
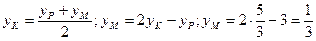

Отже координати точки М 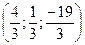 .
.
Задача 5. В задачах 5.1 - 5.30 задані рівняння двох площин
p1: А1х+В1у+С1 z+D1 = 0; p2: А2х+В2у+С2z+D2 = 0; та координати двох точок М1(А1,В1,С1), М2(А2,В2,С2). Значення
А1, В1, С1, D1... А2 ,В2 ,С2, D2 для кожного варіанту приведені в таблиці.
| Номер варіанту | Значення | |||||||
| А1 | В1 | С1 | D1 | А2 | В2 | С2 | D2 | |
| 5.1 | 2+g | 3+g | 1+g | -1-g | ||||
| 5.2 | -2-g | 7+g | 3+g | 5+g | ||||
| 5.3 | -1-g | 5+g | -3+g | 7+g | -8 | |||
| 5.4 | 5+g | -7+g | -2+g | -1+g | -1 | |||
| 5.5 | 3+g | -2+g | 4+g | 2+g | -1 | |||
| 5.6 | 6+g | -4+g | 6+g | 5+g | ||||
| 5.7 | 1+g | 3+g | 7+g | -3+g | ||||
| 5.8 | 8+g | 2+g | -12+g | 5+g | -1 | -3 | ||
| 5.9 | 4+g | 4+g | -6-g | -7+g | -8 | -8 | -4 | |
| 5.10 | 5+g | 5+g | 5+g | 4+g | ||||
| 5.11 | 6+g | 7+g | 2+g | 8+g | -4 | |||
| 5.12 | -1+g | 6+g | -2+g | 4+g | -5 | -1 | ||
| 5.13 | -2+g | 4+g | -1+g | 1+g | -4 | |||
| 5.14 | 7+g | 3+g | 7+g | -7+g | -7 | -1 | -1 | |
| 5.15 | 3+g | -3-g | 5+g | 3+g | -7 | |||
| 5.16 | 4+g | -2-g | 6+g | -4+g | -2 | |||
| 5.17 | 6+g | 11+g | 3+g | -7+g | ||||
| 5.18 | -3+g | 7+g | 9+g | 3+g | -3 | |||
| 5.19 | 5+g | -2+g | 7+g | -8+g | -6 | |||
| 5.20 | 3+g | -1+g | -8+g | -5-g | -4 | -2 | ||
| 5.21 | 2+g | 7+g | 6+g | -4-g | -1 | |||
| 5.22 | 5+g | 5+g | 4+g | 2+g | -6 | |||
| 5.23 | 6+g | 2+g | 6-g | -2+g | -3 | |||
| 5.24 | 2+g | 3+g | 3-g | 8+g | -5 | |||
| 5.25 | 5+g | -3-g | -1-g | 4+g | ||||
| 5.26 | 3+g | 2-g | 8-g | -3+g | ||||
| 5.27 | 1+g | 6+g | 5+g | 3+g | -1 | |||
| 5.28 | 7+g | -2+g | 7+g | -5+g | ||||
| 5.29 | 8+g | 2+g | 3+g | 4-g | ||||
| 5.30 | 4+g | 6+g | -5+g | -7-g |
Потрібно знайти:
1. канонічні та параметричні рівняння прямої, що задана як лінія перетину двох площин p1 та p2;
2. канонічні рівняння прямої, яка проходить через точки
3. величину гострого кута j, який утворює пряма С1С2 з площиною p1.
Методичні вказівки
Розв’язання задачі. Дано такі значення А1=2+у, В1=1+у, С1=-2-у, D1=-3-y, А2=1, В2=-2, D2=2. Тоді якщо у=1, то А1=3, В1=2, С1=-3, D1=-4, А2=1, В2=-2, D2=2. Отже рівняння площин p1 та p2 мають вигляд:
p1: 3x+2y-3z-4=0
p2: x-2y+3z+2=0
а їх нормальні вектори  та
та  , (
, (  ^p1,
^p1,  ^p2).
^p2).
Складемо систему з рівнянь площин p1 та p2
 (1)
(1)
Це буде рівняння лінії перетину площин p1 та p2
1. Для того щоб записати канонічне рівняння прямої (1) у вигляді
 (2)
(2)
Потрібно знайти координати довільної точки М(x0,y0,z0), яка належить цій прямій (1), та координати направляючого вектора  ║Р:
║Р:  . Якщо точка С0 є L, то С0 є p1 та p2. Система рівнянь (1) – це система двох рівнянь з трьома невідомими, яка має безліч розв’язків (тобто пряма має безліч точок). Запишемо (1) у вигляді:
. Якщо точка С0 є L, то С0 є p1 та p2. Система рівнянь (1) – це система двох рівнянь з трьома невідомими, яка має безліч розв’язків (тобто пряма має безліч точок). Запишемо (1) у вигляді:
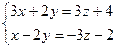
Візьмемо наприклад,z=1, тоді дістанемо 3x+2y=7, x-2y=-5, а звідси
4x=2, 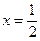 , y=11
, y=11
Отже, шукана точкаС0 
Так як нормальні вектори  перпендикулярні до Р, крім того
перпендикулярні до Р, крім того  ║Р, тому
║Р, тому  перпендикулярні до
перпендикулярні до  . Отже за направляючий вектором
. Отже за направляючий вектором  для прямої Р можна взяти вектор, який дорівнює векторному добутку нормальних векторів
для прямої Р можна взяти вектор, який дорівнює векторному добутку нормальних векторів  , або колінеарній йому:
, або колінеарній йому:
 (3)
(3)
Таким чином, вектор 
Отже канонічні рівняння прямої Р будуть такі:
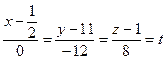
Прирівнюючи кожне відношення до t, дістаємо:
 звідки запишемо параметричні рівняння прямої Р:
звідки запишемо параметричні рівняння прямої Р:
 (4)
(4)
2.Канонічні рівняння прямої, яка проходить через дві задані точки C1(x1,y1z1) та C2(x2,y2z2) мають вигляд:
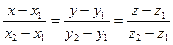 (5)
(5)
Підставляючи в (5) координати точок С1 (3,2,-3) та С 2 (1,-2,3), дістаємо:


звідки (С1 С2):
 (6)
(6)
направляючий вектор якої  ={ 1,2,-3}.
={ 1,2,-3}.
3.Величину куту j, який утворює пряма C1 C2 з площиною p1 можна знайти за формулою:
Sinj 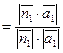
Sinj  (7)
(7)
Підставляючи формулу (7) координати векторів p1={3;2;-3} і  ={1,2,-3}, дістаємо:
={1,2,-3}, дістаємо:
Sinj