Кристаллические и пространственные решетки

РАЗДЕЛ ПЕРВЫЙ

Геометрическая кристаллография.Предмет кристаллографии. Важнейшие свойства кристаллов. Кристаллическая и пространственная решетки. Рост кристаллов. Элементы симметрии кристаллов. Атомные координаты, направления и плоскости в идеальном кристалле. Символы плоскостей (сеток). Переход от параметров Вейсса к индексам Миллера. Кристаллографические категории и сингонии. Решетки Бравэ. Простейшие кристаллографические структуры металлов. Простейшие кристаллографические структуры полупроводников и полупроводниковых соединений. Рентгеноструктурный анализ кристаллов.

Предмет кристаллографии

Кристаллография является наукой о кристаллах и кристаллическом состоянии материи

Важнейшие свойства кристаллов

_________________________________________

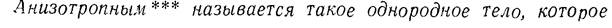
Кристаллические и пространственные решетки

В физике конденсированного состояния одним из наиболее

многочисленных классов веществ являются кристаллические тела.

Какой же смысл вкладывается в понятие кристалл и чем такие

объекты отличаются от некристаллов?

Идеальный кристалл можно построить путем бесконечного

закономерного повторения в пространстве одинаковых структурных

единиц. В наиболее простых кристаллах (например, медь, серебро,

золото) структурная единица состоит из одного атома. В сложных

белковых кристаллах структурная единица может содержать ~104

атомов или молекул.

С каждой точкой этой структурной единицы связана группа

атомов, называемая базисом. Базис повторяется в пространстве и

образует кристаллическую структуру. Отметим отличие терминов

пространственная решетка и кристаллическая структура.

Пространственная решетка -это математическая абстракция -

регулярное расположение точек в пространстве. Тогда как

кристаллическая структура или просто кристалл -это физический

объект, в котором с каждой точкой решетки связан базис –группа

атомов или молекул. Можно записать:

пространственная решетка+базис=кристаллическая структура

(кристалл) (рис. 8.1).

Пространственная решетка Базис Кристалл

Рисунок 8.1 - Процесс образования кристаллической структуры

в двухмерном случае

Часто отождествляют пространственную решетку и

кристаллическую структуру, но в действительности набор реальных

атомов, составляющих базис, можно расположить так, что ни один

атом базиса не будет совпадать с узлами пространственной решетки,

то есть существует некоторый произвол в расположении базиса.

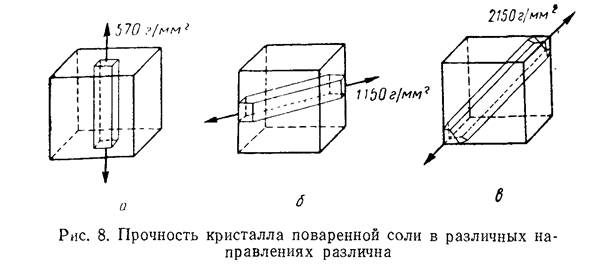
Рассмотрим двухмерную решетку, в которой пространственная

решетка задается следующим образом: существуют два вектора a

и b, для которых выполняется следующее условие: из любой точки

r решетка будет выглядеть абсолютно также, что и из точки r ′, при этом выполняется соотношение:

где n₁, n₂ –целые числа, r, r ′- - радиус векторы двух узлов решетки.

Такие векторы a , b носят название векторов трансляции, то есть

векторы, соединяющие узлы кристаллической решетки (рис.8.2).

Модули этих векторов называют параметрами решетки.

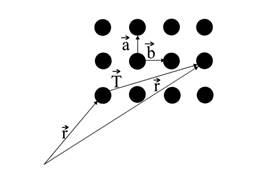
Рисунок 8.2 - Двумерная решетка. Здесь Т вектор трансляции

Рассмотрим трехмерный случай

Любой вектор T называется вектором трансляции, а соответствующая ему операция перемещения по кристаллу – операцией трансляции.

Чтобы изобразить кристаллическую решетку часто используют понятие элементарной ячейки, под которой понимают минимальную часть решетки, обладающую ее симметрией, и повторением которой с помощью векторов трансляции можно получить всю решетку (рис. 8.3).

Рисунок 8.3 - Элементарная ячейка кристаллической решетки

(заштрихована)

Выбирать элементарную ячейку можно большим количеством способов, удовлетворяя при этом всем условиям, перечисленным выше. На рис. 8.4 представлены разные элементарные ячейки. Легко увидеть, что с помощью векторов трансляции можно покрыть элементарными ячейками всю решетку. Среди элементарных ячеек выделяют также примитивную элементарную ячейку – это элементарная ячейка с минимально возможным объемом (элементарная ячейка, содержащая один атом). Для описания кристаллических структур пользуются как примитивными, так и не примитивными ячейками (когда они более удобны, и пользоваться ими проще).

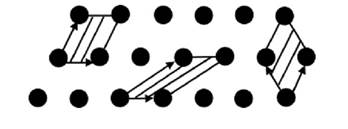
Рисунок 8.4 - Произвол в выборе элементарной ячейки в

двухмерном случае

Частным случаем элементарной ячейки является ячейка Вигнера-Зейтца, которая строится особым образом, но сохраняет в себе все черты элементарной ячейки, перечисленные выше. Ввиду частого использования в физике такого типа ячейки подробно опишем процесс ее построения (рис.8.5). Вначале соединим отрезками данный узел решетки со всеми соседними узлами. Через середины отрезков проведем линии (в трехмерном случае – плоскости) перпендикулярные этим отрезкам. Полученные линии или плоскости, пересекаясь, создают некоторые фигуры. Фигура минимального объема, полученная таким образом, и есть ячейка Вигнера-Зейтца.