ОСОБЕННОСТИ ПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ В СИСТЕМЕ MATLAB

Стр 1 из 4Следующая ⇒

ЦЕЛЬ РАБОТЫ

1.1 Изучение метода переходных функций (характеристик).

1.2 Ознакомление с методом наименьших квадратов (МНК).

1.3 Ознакомление с понятием идентификации промышленных элементов САУ.

1.4 Ознакомление с понятием аппроксимации переходной характеристики.

1.5 Ознакомление с понятием оценки адекватности математической модели.

1.6 Ознакомление с понятием активный эксперимент.

СОДЕРЖАНИЕ РАБОТЫ

2.1 Экспериментальное исследование исполнительного механизма (ИМ).

2.2 Идентификация ИМ. Построение простой линейной регрессионной модели ИМ.

2.3 Экспериментальное исследование объекта регулирования (ОР).

2.4 Идентификация ОР. Построение нелинейной регрессионной модели ОР.

ОБЩИЕ СВЕДЕНИЯ

Идентификацией динамической системы называют получение или уточнение по экспериментальным данным математической модели (ММ)
этой системы. ММ может быть выражена обыкновенным дифференциальным уравнением (ОДУ) или передаточной функцией (ПФ). Получение ММ в таком виде составляет задачу непараметрической идентификации. Параметры модели являются результатом параметрической идентификации.

Классическими методами непараметрической идентификации линейных САУ или ее элементов являются:

– метод временных характеристик;

– метод частотных характеристик;

– метод корреляционных функций.

К прямым методам параметрической идентификации относят:

– метод наименьших квадратов;

– метод сумм произведений и др.

Выбор того или иного метода идентификации и оценки параметров ММ зависит от априорной информации об объекте исследования и требованиях, предъявляемых к ММ. На практике чаще используют метод временных характеристик как более простой в организации эксперимента. Если эксперимент проводят для получения переходной характеристики h(t), метод называют методом переходных характеристик (функций). Традиционно объединяют метод переходных характеристик с регрессионным анализом, основу которого составляет метод наименьших квадратов (МНК). Созданная таким образом ММ является регрессионной моделью, качество которой гарантированно статистически.

Сущность метода переходных характеристик заключается в следующем. До начала эксперимента изучают объект идентификации и разрабатывают программу его исследования, а также оценивают возможность считать объект линейным, стационарным, с сосредоточенными параметрами. Названные допущения позволяют описать динамические свойства исследуемого объекта ОДУ

(1)

или передаточной функцией

(2)

где а_n, a_n_-1,..., a₀, b_m, b_m_-1,…, b₀ – постоянные коэффициенты (n m).

Если объектом идентификации является элемент САУ, то по его физическим свойствам предварительно выбирают ММ из числа типовых динамических звеньев (ДЗ). Затем проводят активный эксперимент. Для этого сначала приводят исследуемый объект в исходное установившееся состояние. После этого ступенчато изменяют входное воздействие на Dx и регистрируют соответствующее изменение во времени выходной величины Dy = f(t). Эту зависимость называют разгонной характеристикой и обозначают y(t). По достижении объектом нового установившегося состояния прекращают эксперимент. При испытании астатических объектов под установившимся состоянием понимают постоянную скорость изменения выходной величины (рисунок 1). Статические объекты в установившемся состоянии отличаются постоянством выходной величины, т.е. y(t)=const. Полученную экспериментально разгонную характеристику y(t) аппроксимируют теоретической переходной функцией h(t). Эта функция является решением ОДУ, принятого в качестве ММ объекта идентификации. Аппроксимирующую переходную функцию h(t) выбирают первоначально из переходных функций типовых ДЗ (см. таблицу 1 Отчета о выполнении лабораторной работы №1) при условии наибольшего соответствия характеристик y(t) и h(t) друг другу. Типовое ДЗ, переходная функция которого выбрана в качестве аппроксимирующей, таким образом, принимается в качестве ММ исследуемого объекта. Определяется порядок n ОДУ, решением которого является аппроксимирующая характеристика h(t). Уравнение характеристики h(t) записывают в явном виде, например, (5) или (16). В этом уравнении неизвестными остаются только коэффициенты. Их находят решением обратной задачи: по известным значениям функции y(t) и соответствующим им значениям аргумента (времени t) рассчитывают неизвестные коэффициенты. Эта задача является оптимизационной в том смысле, что искомые коэффициенты должны обеспечить минимум расхождения между характеристиками h(t) и y(t). В качестве критерия расхождения чаще всего принимают минимум суммы квадратов ошибок по всей совокупности измерений

Этот метод называют методом наименьших квадратов (МНК). С его помощью строят уравнение регрессии h(t), которым аппроксимируют разгонную характеристику y(t). Такое уравнение часто называют регрессионнной моделью.

Идентификация будет полной, если будет доказана значимость принятой ММ. Названную модель считают значимой, если расхождение между характеристиками h(t) и y(t) является незначительным в статистическом смысле. Оценку значимости уравнения регрессии в целом проводят по F-критерию Фишера. При положительном результате проверки уравнения регрессии оценивают значимость его коэффициентов по t-критерию Стьюдента. Одновременно коэффициенты уравнения регрессии (регрессионной модели) являются коэффициентами ММ.

При идентификации типовых элементов САУ методом переходных характеристик аппроксимирующие характеристики h(t) большей частью получают в виде прямых линий (рисунок 1) или экспонент (рисунок 2), а также их совокупности. Переходные характеристики П- и И- звеньев являются линейными. Экспонентой является переходная характеристика А-звена первого порядка; экспонента также является частью характеристики реального Д-звена и т.д.

Методом наименьших квадратов можно построить линейную регрессию y на x

(3)

и нелинейную

(4)

В рассматриваемом случае идентификации элемента САУ отклик y – выходная величина этого элемента , фактор x– время t. При ручном сборе данных эксперимента наблюдения заносят в таблицу 1 или изображают графически.

Таблица 1-Первичные данные активного эксперимента

y	y₁	y₂	y₃	y₄	y₅	y₆	y₇
t	t₁	t₂	t₃	t₄	t₅	t₆	t₇

На графике (scatter plot) каждому наблюдению соответствует точка с координатами yiи ti(рисунки 1 и 2). В совокупности они образуют облако точек. В отличии от таблицы расположение точек облака указывает на вид искомой функциональной зависимости h(t). Если точки расположены так, как показано на рисунке 1, то экспериментальную зависимость аппроксимируют прямой линией h(t). Таким образом, результаты эксперимента yi(ti) могут быть аналитически описаны уравнением линейной регрессии

(5)

Свободный член b₁ и угловой коэффициент b₂ уравнения линейной регрессии рассчитывают вручную или с помощью ПК.

Рассчитывают также несмещенную оценку дисперсии теоретического распределения наблюдений yi

(6)

и остаточную дисперсию

. (7)

Эти величины служат для оценки статистической значимости полученного уравнения регрессии по F-критерию Фишера

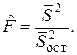(8)

При этом поступают следующим образом. Во-первых, формулируют две гипотезы. Первую, так называемую нуль-гипотезу H₀:b₁=0, о том, что регрессия y на x отсутствует (у не зависит от х). Вторую, альтернативную, H₁:b₁≠0.Во-вторых сравнивают рассчитанный по (8) F-критерий Фишера с критическим значением F^T. Если

, (9)

нуль-гипотезу отклоняют и уравнение регрессии (5) считают значимым. Если нуль-гипотезу принимают. Это означает, что наилучшей оценкой при любых будет среднее значение .

В данном случае значимость характеризует качество исследуемой модели (5). Считают, что при выполнении неравенства (9) никакая другая регрессионная модель (например, полиноминальная) не лучше простой линейной регрессии (5).

В случае положительной оценки значимости уравнения регрессии в целом возможно оценить также значимость коэффициентов регрессии. Выдвигается нуль-гипотеза H₀:b₁=0 о том, что “истинное” значение свободного члена равно нулю, и нуль-гипотеза H₀:b₂=0 о том, что угловой коэффициент b₂ равен нулю. Формулируют также альтернативные гипотезы H₁:b₁≠0 и H₁:b₂≠0. проверку нуль-гипотез осуществляют по t-критерию Стьюдента. Коэффициенты уравнения регрессии статистически значимы и нуль-гипотезу отвергают при

; (10)

где – критическое значение.

В противном случае нет оснований для отклонения нуль-гипотезы, т.е. предположение о значимости коэффициентов b₁ и b₂ отвергается. К такой ситуации приводит использование идеального И-звена с передаточной функцией в качестве ММ какого-либо элемента САУ (например, исполнительного механизма). Идентификация такого элемента заключается в определении коэффициента передачи K или постоянной времени T = 1/K И-звена. Результаты испытания элемента показаны на рисунке 1 в виде облака точек yi(ti). Обращает на себя внимание первая точка y₁ = 0 и t₁ = 0. Но линия регрессии может начинаться и в другой точке. Это означает, что по расчету свободный член уравнения регрессии отличен от нуля (b₁ ¹ 0). Другими словами, проверяется гипотеза о значимости в статистическом смысле коэффициентов регрессии b₁ и b₂. Для проверки этой гипотезы рассчитывают и и сравнивают с критическим значением . Считать свободный член b₁ незначимым можно лишь при условии, что . В этом случае его можно исключить из уравнения регрессии, которое принимает вид

h(t) = bt. (11)

Сравнивая уравнение построенной регрессии h(t) = bt с переходной функцией идеального И-звена h(t) = Kt, принимают коэффициент передачи И-звена K равным угловому коэффициенту уравнения регрессии b.

Завершающим этапом идентификации элемента считают исследование остатков. Под остатками (Residuals) понимают разности между наблюдаемыми и предсказанными значениями :

. (12)

Анализ остатков позволяет оценить качество регрессионной модели. Согласно общим предположениям регрессионного анализа , остатки должны вести себя как независимые одинаково распределенные случайные величины. Классический регрессионный анализ требует нормального закона распределения остатков. Это предположение необходимо для применения F-критерия. В связи с этим анализ остатков включает:

- проверку статистической гипотезы о нормальном распределении значений

r_i ;

- проверку гипотезы о статистической независимости значений r_i.

Названные задачи решают графически или аналитически. Оба способа содержат несколько вариантов решения задачи.

Для проверки нормальности распределения остатков r_i необходимо построить гистограмму остатков (Histogram) или нормальный вероятностный график (Normal probability plot). Эту же проверку аналитически осуществляют с помощью критериев согласия хи-квадрат(chi-square), Колмогорова-Смирнова, омега - квадрат, а также по коэффициентам асимметрии (Skewness) и эксцесса (Kurtosis).

Для проверки независимых остатков используют критерий серий и критерий Дурбина-Уотсона.

Каждая математическая система МАTLAB, MathСAD, Maple, Mathemаtica содержит статистические функции для регрессионного анализа, а системы MATLAB и Mathemаtica пакеты расширения Curve Fitting Toolbox, Statistics Toolbox и Statistics. Графические интерфейсы последних существенно облегчают пользователю подбор кривых (fitting) и оценку значимости ММ без какого-либо программирования задачи.

Однако наряду с названными инструментами существуют средства профессиональной статистической обработки данных: Statistica [1,3] , SPSS [4,14], StatGraphics [8], STADIA [11] c руководствами для пользователя на русском языке. Более того, система STADIA представляет собой российский продукт. Эти системы отличаются более “мощными” средствами анализа данных по сравнению с математическими системами MATLAB и т.п. Выше и уровень обслуживания пользователя, все запросы которого удовлетворяются посредством меню. Есть и другие преимущества специализированных систем перед универсальными. Тем не менее последние системы, особенно MATLAB, позволяют пользователю решать очень широкий спектр типовых задач ТАУ, лишь одной из которых является задача идентификации.

ОСОБЕННОСТИ ПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ В СИСТЕМЕ MATLAB

4.1 Построение линейной регрессии

Уравнение простой линейной регрессии имеет следующий вид:

(13)

где - зависимая величина (отклик);

х - независимая величина (фактор);

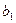- свободный член уравнения регрессии (intercept);

- угловой коэффициент уравнения регрессии (slope).

Исходными данными для построения уравнения линейной регрессии (13) служат результаты прямого эксперимента (наблюдения) , сведенные в таблицу 1. Задача регрессионного анализа состоит в определении коэффициентов регресси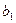и и , при которых уравнение регрессии (13) наилучшим образом описывало бы результаты эксперимента.

Табличные данные вводят в MATLAB в режиме командной строки в виде двух векторов х и у одинакового размера согласно SCRIPT 1.

SCRIPT 1:

>> x=[1 2 3 4 5];

>> y=[4 5 6 7 8];

>> plot(x,y,'o')

Выполнение последней команды plotоткрывает графическое окно Figure№1с диаграммой рассеяния (облаком точек). Никаких ограничений на вид зависимости MATLAB не накладывает. Если названная зависимость по внешнему виду близка к линейной, то с помощью мыши следует выполнить следующие команды ToolsиBasiс Fitting.В открывшемся окне Basic Fitting-1необходимопоставить птичку около Linearи Show equation, а затем наблюдать в основном окне Basic Fitting-1линию регрессии и уравнение регрессии с численными значениями коэффициентов b₁и b₂. Дополнительные статистические сведения о величинах x и y можно получить в окне Data Statistics-1,которое открывается командами Toolsи Data Statistics.

Подобный результат можно получить, используя функцию rstoolсогласно SCRIPT 2.

SCRIPT 2:

>> x=[1;2;3;4;5];

>> y=[4;5;6;7;8];

>> rstool(x,y,'interaction')

Эта команда открывает диалоговое окноFigure№1:Prediction Plot of Linear Model, содержащее диаграмму рассеяния и линию регрессии, а также доверительные интервалы. Для вывода в рабочее пространство MATLAB коэффициентов уравнения регрессии следует нажать кнопку Exportи в выпадающем меню выбрать Parameters.В открывшемся подокне настройки MATLAB предлагает командуbetaдля вывода искомых параметров в командную строку. Согласие подтверждают нажатием кнопки ОК.Подокно закрывается. Необходимо закрыть и графическое окно Figure№1,а в командной строке ввести команду beta согласно SCRIPT 3.

SCRIPT 3:

>> beta

beta =

3.0000

1.0000

Третий вариант визуализации линии регрессии реализуется функцией lsline в следующем порядке.

SCRIPT 4:

>> x=[1 2 3 4 5];

>> y=[4 5 6 7 8];

>> plot(x,y,'+');

>> lsline

Названные варианты позволяют только провести прямую линию регрессии, которая аппроксимирует результаты эксперимента. Оценку значимости уравнения регрессии в целом, а также оценку значимости коэффициентов этого уравнения можно получить с помощью функцииglmfit.Свое название функция получила от слов generalized linear model fitting , т.е. выравнивание с помощью обобщенной линейной модели. Следующий SCRIPT показывает особенности названной функции.

SCRIPT 5:

>> x=[0 1 2 3 4 5 6 7 8 9];

>> y=[0 1.0107 2.0006 2.9990 3.9917 5.0029 5.9866 7.0071 8.0162 8.9931];

>> [b,dev,stats]=glmfit(x,y)

b =

0.0013

0.9999

dev =

7.2604e-004

stats =

beta: [2x1 double]

dfe: 8

sfit: 0.0095

estdisp: 1

s: 0.0095

se: [2x1 double]

coeffcorr: [2x2 double]

t: [2x1 double]

p: [2x1 double]

resid: [10x1 double]

residp: [10x1 double]

residd: [10x1 double]

resida: [10x1 double]

Очевидно, что первыми возвращаются исходные коэффициенты уравнения регрессии b₁=0.0013 и b₂=0.9999, содержащиеся в векторе b.

Величина dev(deviance) есть сумма квадратов отклонений выборочных значений от их среднего значения , т.е

Под именем статистик (stats) объединены:

beta - стандартизованные коэффициенты уравнения регрессии;

dfe - количество степеней свободы;

sfit - estimated dispersion parameter;

se - стандартные ошибки коэффициентов регрессии;

coeffcorr - коэффициент корреляции;

t - t-статистики коэффициентов уравнения регрессии;

p - уровень значимости;

resid – вектор остатков.

Полученные данные служат для непосредственной оценки качества регрессионной модели путём последовательной проверки ряда гипотез.

4.2 Проверка гипотезы нормальности остатков

Первой проверяется гипотеза о нормальном распределении остатков. Сначала просматривают остатки согласно SCRIPT 6.

SCRIPT 6:

>> [stats.resid]

ans =

-0.0013

-0.0095

-0.0004

-0.0019

-0.0091

0.0022

-0.0140

0.0066

0.0158

-0.0072

Просмотр показывает, что получены остатки обоих знаков, среди которых явных выбросов нет. В этом случае сразу проверяют нормальность распределения остатков. Вводя собственное обозначение остатков r, с помощью функции histfitстроят гистограмму остатков согласно SCRIPT7.

SCRIPT 7:

>> r=ans;

>> histfit(r)

На экран монитора в графическом окне Figure№1 выводятся столбцовый график остатков и теоретическая кривая нормального распределения (рис.3). Близость сходства двух графиков отражает меру соответствия реального распределения остатков идеальному теоретическому. При малом количестве наблюдений (как в рассматриваемом примере n=10) следует ожидать лишь приближенного подобия указанных графиков.

Рисунок 3

Аналогично рассмотренную проверку проводят с помощью нормального вероятностного графика , который строят с помощью функции normplot согласно SCRIPT 8.

SCRIPT 8:

>> normplot(r)

На экран монитора в графическом окне Figure№1 выводятся остатки и прямая линия (рис.4). Если изображения остатков “притягиваются” к отрезку непрерывной прямой между 25% и 75%, то гипотезу нормального распределения остатков считают подтвержденной.

Рисунок 4

Более строгую оценку допустимости рассматриваемой гипотезы получают аналитически с помощью критериев согласия.

Пакет расширения Statistics Toolbox содержит следующие функции: chitest (критерий Пирсона или х²), jbtest (критерий Жако-Бера), kstest (критерий Колмогорова-Смирнова), lillietest (критерий Лилиефорса). Для исследования малых выборок , к которым относится рассматриваемый пример с n=10, необходимо использовать критерий Лиллиефорса. SCRIPT 9 показывает простейший вариант обращения к соответствующей функции lillietest.

SCRIPT 9:

>> H=lillietest(r)

Если получен результат H=1, гипотеза о нормальном распределении остатков может быть отклонена. В противном случае , когда Н=0, нет оснований для отклонения гипотезы.

Таким образом , три равноценных варианта проверки достоверности гипотезы о нормальном распределении остатков линейной регрессии дают положительный результат. На практике считают достаточным использование только одного из рассмотренных вариантов.

4.3 Проверка гипотезы независимости остатков

Второй проверяется гипотеза независимости остатков. Statistics Toolbox средств осуществления названной проверки не содержит. Поэтому достоверность этой гипотезы возможно осуществить с помощью обычных математических функций MATLAB. В основу критерия Дурбина-Уотсона положена статистика d, которую необходимо вычислить по формуле [2,6]

. (14)

Упрощенная процедура проверки гипотезы отсутствия сериальной корреляции между остатками сводится к следующему: если или то гипотеза отвергается на уровне значимости 2α(α=5%, α=2,5% или α=1,0%). Критические значения , соответствующие указанным уровням значимости , при минимальном n=15 равны d_5.0^T=1.35, d_2.5^T=1.23 и d_1.0^T=1.07.

Для оценки некоррелируемости остатков рассматриваемого примера , образующих вектор остатков r (см. SCRIPT 6 и SCRIPT 7), необходимо создать в MATLAB векторы r₁ и r₂. Оба вектора легко получить изменением вектора остатков r. Очевидно , что r₁ получают исключением первого элемента r₁=-0.0013 вектора r, т.к. i=2. Наоборот , вектор r₂ образуют исключением последнего элемента r₁₀=-0.0072 вектора r. Затем рассчитывают статистику d, см. SCRIPT 10.

SCRIPT 10:

>> r=r'

-0.0013 0.0095 -0.0004 -0.0019 -0.0091 -0.0022 -0.0140 0.0066 0.0158 -0.0072

>> r1=[0.0095 -0.0004 -0.0019 -0.0091 -0.0022 -0.0140 0.0066 0.0158 -0.0072];

>> r2=[-0.0013 0.0095 -0.0004 -0.0019 -0.0091 -0.0022 -0.0140 0.0066 0.0158];

>> d=sum((r1-r2).^2)/sum(r.^2)

2.3371

Сравнение полученного результата d=2.3371 с критическим значением d^T=1.35 свидетельствует об отсутствии сериальной корреляции остатков.

4.4 Проверка значимости регрессионной модели

Третьей проверяется гипотеза о статиcтической значимости уравнения регрессии =0,0013+0,9999*x в целом. В Statistics Toolbox нет функции , которая бы позволила выполнить проверку в одно действие. В связи с этим один вариант проверки заключается в расчете F-отношения по формуле (8). Предварительно вычисляют оценки дисперси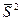й и по формулам (6) и (7) соответственно. Второй , более короткий и простой вариант расчета F-отношения, основан на следующей связи t-статистик и F-отношения

, (15)

которую часто используют при анализе линейной регрессии. Согласно SCRIPT 5 названные t-статистики коэффициентов регрессии содержит вектор-столбец t. Их значения t_b₀=0.2244 и t_b₁=953.3356 возвращаются командой stats.t. Значение F-критерия Фишера рассчитывают по формуле (15).
Затем с помощью функции finv(p,υ1,υ2) определяют критическое значение F^T,где р-вероятность вывода (обычно р=0.95), υ₁ и υ₂– количество степеней свободы (υ₁=n-1, υ₂=n-2, n-количество наблюдений). В рассматриваемом примере υ₁=9 и υ₂=8, т.к. n=10. Таким образом , для проверки гипотезы о значимости линейной регрессионной модели необходимо выполнить действия согласно SCRIPT 11.

SCRIPT 11:

>> stats.t

ans=

0.2244

953.3356

>> tb2=953.3356;

>> F=tb2^2

90885е+005

>> FT=finv(0.95,9,8)

FT=3.3881

Окончательный результат F=908849>>F^T=3.3881 серьёзно свидетельствует в пользу гипотезы о значимости полученного уравнения регрессии.

В случае F<F^T названную гипотезу следует отклонить. После этого целесообразно вернуться к исследованию остатков регрессии.

Исследование остатков рекомендуют начинать с изучения их графика

или , который получают с помощью функции plot(x,r,’o’). Если остатки расположены в горизонтальной полосе с центром на оси абсцисс , регрессионную модель рассматривают как значимую (рис.5).

Рисунок 5

В противном случае он указывает на наличие некоторой зависимости , не учитываемой моделью. В частности, график остатков может показать необходимость перехода к нелинейной модели или включения в модель периодических составляющих.

4.5 Проверка значимости коэффициентов регрессии

Четвёртой проверяется гипотеза о статистической значимости коэффициентов регрессии b₁ и b₂. Для оценки значимости коэффициентов уравнения регрессии b₁ и b₂следует ввести к командной строке

SCRIPT 12:

>> [b stats.t stats.p]

ans

0.0013 0.2244 0.8281

0.9999 953.3356 0.0000

В первом столбце возвращаются коэффициенты b₁=0.0013 и b₂=0.9999; во втором t-статистики названных коэффициентов t_b₁=0.2244 и t_b₂=953.3356 и в третьем соответствующие уровни значимости p_b₁=0.8281 и p_b₂=0.0000. Приняв последние два значения в качестве критических t_b₁^T=p_b₁=0.8281 и t_b₂=p₂=0.0000, сравнивают их с t-статистиками соответственно

t_b1=0.2244 < t^T=0.8281;

t_b2=953.3356 >> t^T=0.0000.

Таким образом, нет оснований считать свободный член регрессии b₁ значимым в статистическом смысле. Он может быть исключен из уравнения регрессии. Напротив, угловой коэффициент отличается очень высокой значимостью.

Эту же гипотезу можно проверить графически с помощью уже известной функции rstool.В графическом интерфейсе этой функции кроме линии регрессии отображаются границы доверительного интервала (красные пунктирные линии). Если этот интервал включает начало координат , гипотезу о значимости свободного члена уравнения регрессии отклоняют и считают b₀=0 [2].

В связи с этим окончательно принимают уравнения регрессии в виде

или

4.6 Построение нелинейной регрессии

Встроенные функции nlintoolи nlinfitиз пакета расширения Statistics Toolbox предназначены для построения нелинейной регрессии любой формы. Первая из названных функций nlintoolаналогична рассмотренной ранее функций rstool. Подобие заключается в графическом интерфейсе пользователя, который позволяет проводить интерактивный анализ построенной регрессии. Но обращение к функции nlintoolсложнее в связи с необходимостью ввода в программу уравнения нелинейной регрессии, а также необходимостью указать начальные значения коэффициентов регрессии.

Простейшим примером нелинейной регрессии является экспоненциальная. К такого рода зависимостям приходят при идентификации элементов САУ, в качестве ММ которых принимают инерционное звено (А-звено первого порядка, см. лабораторную работу №1). Как известно, переходная характеристика этого звена изображается экспонентной и описывается уравнением

(16)

где K - коэффициент передачи и Т- постоянная времени А-звена. В этом случае искомыми являются величины К и Т. Известна переходная характеристика, полученная экспериментально. Дискретные значения этой зависимости y_i и х_i сведены в таблицу 2.

Таблица 2-Первичные данные активного эксперимента

x
у	0.368	0.135	0.050	0.018	0.007

На рисунке 2 изображено соответствующее “облако” точек. На этом же рисунке по точкам необходимо от руки нарисовать экспоненту, а затем методом касательной определить постоянную времени Т и рассчитать коэффициент передачи

В данном случае Т=1.1 и К=0.9. Эти величины являются элементами вектора начальных значений параметров регрессионной модели b0=[K T]. Для ввода в MATLAB уравнения регрессии под именем fun(от function) используется встраиваемая функция inline.

Таким образом, построение экспоненциальной регрессии характеризуется SCRIPT 13.

SCRIPT 13:

>> x=[1 2 3 4 5];

>> y=[0.368 0.135 0.050 0.018 0.007];

>>b0=[0.9 1.1];

>> fun=inline(’b(1)*exp(-x/b(2))’,’b’,’x’)

fun=

Inline function:

fun(b,x)= b(1)*exp(-x/b(2))

>>nlintool(x,y,fun,b0)

В результате обращения к функции nlintoolна экране монитора открывается графическое окно Figure№1:Nonlinear fit of b(1)*exp(-x/b(2)),

cодержащее искомую линию регрессии (зелёная экспонента) и границы доверительного интервала (красные пунктирные линии). Чем уже названный интервал , тем выше качество регрессионной модели.

Искомые коэффициенты регрессии b₁ и b₂получают последовательно в два приёма. Во-первых , не закрывая и не сворачивая графического окна , активизируют кнопку Exportи в выпадающем меню выделяют первую позицию Parameters.В появившемся подокне настройки указана команда beta, предназначенная для вывода на экран в командной строке коэффициентов b₁ и b₂ . MATLAB допускает изменить наименование этой команды на любое другое, например alfa. Проще сохранить предложенное наименование beta , подтвердив этот выбор нажатием кнопкиОК.После закрытия подокна необходимо свернуть графическое окно Figure№1.Во-вторых , в командной строке вводят в MATLAB рассмотренную команду beta, которая возвращает коэффициенты уравнения регрессии b₁ и b₂ соответственно SCRIPT 14.

SCRIPT 14:

>>beta

beta=

1.0015

0.9987

Для исследования остатков их предварительно выводят на экран в только-что рассмотренной последовательности (Export и далее) при помощи команды residuals.

Коэффициенты уравнения регрессии и остатки возвращает также функция nlinfit, к которой обращаются согласно SCRIPT 15.

SCRIPT 15:

>>[beta,r]=nlinfit(x,y,fun,b0)

beta=

1.0015

0.9987

1.0e-003*

0.0353

-0.1967

0.3264

-0.2510

0.2943

Отличается эта функция от функции nlintoolотсутствием графического интерфейса.

4.7 Проверка качества экспоненциальной регрессии

Проверку качества регрессионной модели

проводят в той же последовательности, в которой исследовалась линейная регрессионная модель. Но при этом недопустимо использовать функцию glmfit , т.к. возвращаемые статистики характеризуют линейную модель. В связи с этим для оценки адекватности регрессионной модели F-критерий Фишера рассчитывают по формуле (8) и сравнивают его с критическим значением F^T, которое определяют с помощью функции finv согласно со SCRIPT 11.

12 3 4 Следующая ⇒