Главная | Обратная связь

Переходные характеристики цепей первого порядка.

Цепи первого порядка содержат только один энергоемкий элемент – емкость или индуктивность – и описываются дифференциальными уравнениями первого порядка. Откликом можно считать ток в любой интересующей нас ветви или напряжение на любом интересующем нас элементе. Соответственно, можно рассматривать различные переходные характеристики.

Интегрирующая RC-цепь.

Цепь, состоящая из RC-элементов и приведенная на рис. 5.1 называется интегрирующей RC-цепью.

Рис. 5.1

Установим связь между выходным u₂ и входным u₁ напряжениями, считая входной сигнал u₁ произвольным. Используя второй закон Кирхгофа и соотношения между напряжениями и токами на элементах схемы, запишем:

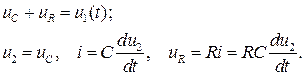
Подставим полученные напряжения в первое выражение:

.

Если R 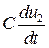>> 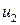, то R 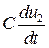= или .

Последнее означает, что выходной сигнал есть интеграл от входного сигнала. Отсюда и название этой цепи – интегрирующая цепь.

Рассмотрим по входному сигналу два частных случая.

А). Переходная характеристика. Пусть входной сигнал – ступенчатое напряжение амплитудой Е (рис. 5.2) . Используя классический метод, определим отклик цепи при нулевых начальных условиях.

1) Составим дифференциальное уравнение и приведем его к стандартному виду

.

2) Запишем общее решение:

u₂(t) = A×e^pt + u₂(¥)

3) Найдем коэффициент р – корень характеристического уравнения

RCр + 1 = 0.

Отсюда р = – (RC)^–1.

4) Найдем вынужденную составляющую общего решения

u2(0) = 0 а б E u2(¥) = E E

Рис.5.3

Вынужденную составляющую находим в стационарном (установившемся) режиме, который имеет место, когда t ® ∞. В этом случае входной сигнал – постоянное напряжение величины , ему соответствует гармонический сигнал с нулевой частотойω = 0, так как = cos ωt|_(ω=0). При таких условиях наличие индуктивности равносильно короткому замыканию (Х_L = ωL), а емкости – разрыву цепи (Х_С = (ωС)^–1).

Для нахождения вынужденной составляющей составим схему замещения исходной цепи при ω = 0 (рис. 5.3а). Из схемы следует, что u₂(¥) = Е.

Отсюда р₁= –(RC)^–1.

5) Найдем постоянную интегрирования A.

Ее находим из общего решения при t ® 0 и схемы замещения исходной цепи при t ® 0 (ω ® ∞) (рис.5.3б). Запишем уравнение, откуда и найдем А

u₂(0)=A +E =0; A = –E.

6) Запишем общее решение:

.

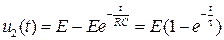Выходное напряжение представляет собой импульс, характеризующийся двумя параметрами: амплитудой Е и постоянной времени цепи τ=RC.

0,63 E t2 t1 t E

Рис. 5.4

Определим выходной сигнал при t = τ:

.

Отсюда следует, что постоянная времени – это время, за которое импульс, возрастая по экспоненциальному закону, изменяется от 0 до уровня 0,63 от своего стационарного значения Е (рис. 5.4).

0,63E

Иногда пользуются третьим параметром. t_уст – время установления выходного напряжения. Это время, за которое сигнал достигает своего стационарного значения с заданной точностью от амплитуды импульса. Так, время установления на уровне 0,9 и 0,95 составляет t_{уст 0,9} = 2,3τ; t_{уст 0,95} = 3τ.

Переходная характеристика выходного напряжения h_u2 по определению равна

Переходная характеристика входного тока будет, соответственно,

С(du_Cc/dt)/E=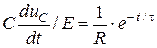

При воздействии ступенчатым напряжением h_i имеет размерность проводимости и называется переходной проводимостью.

Б). Отклик на прямоугольный импульс (рис. 5.5) амплитудой Е и длительностью t_и. Такой импульс представляет собой суперпозицию двух ступенчатых сигналов и записывается как

.

E t u1	t >> tи t ~ tи E E u2 u1 u1 u1 u2 t << tи u2 t t t E в б а
	Рис. 5.5	Рис. 5.6

Зная отклик на ступенчатый сигнал и используя принцип суперпозиции, можно записать аналитическое выражение для выходного сигнала:

R L

Рис. 5.7

.

На рис. 5.6 показаны три временных диаграммы выходного сигнала при различных соотношения между τ и t_и.

Аналогичными свойствами обладает цепь, состоящая из RL-элементов (рис. 5.7). Она называется интегрирующей RL-цепью. Постоянная времени этой цепи t=L/R.

 

Дифференцирующая RC-цепь

Рассмотрим RC-цепь, представленную на рис.5.8, на вход которого подается ступенчатое напряжение амплитудой Е: (рис. 5.2). Используя классический метод, определим отклик цепи при нулевых начальных условиях.

Используя второй закон Кирхгофа и соотношения (5.1), устанавливающие связь между напряжениями и токами на элементах схемы, запишем

Подставим полученные напряжения в первое выражение, умножим на RC и продифференцируем один раз по времени

Если в этом соотношении считать, что . Последнее означает, что выходной сигнал есть производная от входного сигнала, поэтому эта цепь называется дифференцирующей цепью.

Общее решение уравнения имеет вид

u₂(t) = A×e^pt + u₂(¥)

Коэффициент р является корнем характеристического уравнения

RCр + 1 = 0.

Отсюда р = – (RC)^–1.

Вынужденную составляющую находим в стационарном (установившемся) режиме, когда t ® ∞. В этом случае входной сигнал – постоянное напряжение величины , ему соответствует гармонический сигнал с нулевой частотойω = 0, так как E = E cos ωt|_(ω=0). При таких условиях наличие индуктивности равносильно короткому замыканию (Х_L = ωL), а емкости – разрыву цепи (Х_С = (ωС)^–1).

Для нахождения вынужденной составляющей составим схему замещения исходной цепи при ω = 0 (рис. 5.9). Из схемы следует, что u₂(∞)= 0.

 

Найдем постоянную интегрирования A.

Постоянные интегрирования находят из начальных условий для искомой функции и ее производных (при t = +0). Значения токов и напряжений в начальный момент времени после коммутации (при t = +0) определяют из схемы замещения исходной цепи, образованной после коммутации (с учетом законов коммутации) по законам Кирхгофа. При нулевых начальных условиях наличие индуктивности равносильно разрыву цепи (i_L(–0)=i_L(+0)=0), а емкости – короткому замыканию (u_c(–0) = u_c(+0)=0).

Аналогичную схему замещения можно получить, если считать, что ступенчатому сигналу в начальный момент времени (t=+0) соответствует гармонический с бесконечно большой частотой (ω ® ∞).

Для дифференцирующей RC-цепи схема в момент после коммутации (при t = +0, ω ® ∞) приведена на рис. 5.10, а постоянную A находят подставляя в общее решение t=0 и u₂(¥):

Рис. 5.11

u₂(0)=A₁= .

6) Запись общего решения:

.

Выходное напряжение представляет собой экспоненциальный импульс, который характеризуется двумя параметрами (рис.5.11):

1) Е – амплитуда импульса;

2) τ – постоянная времени цепи. Определим выходной сигнал при t = τ.

.

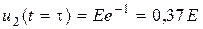Отсюда следует, что постоянная времени – это время, за которое импульс, убывая по экспоненциальному закону, изменяется от Е до уровня 0,37Е (т.е. убывает в е = 2,71 раза).

Иногда пользуются третьим параметром: t_уст – время установления выходного напряжения, это время, за которое сигнал достигает своего стационарного значения с заданной точностью от амплитуды импульса. Так, время установления на уровне 0,1 и 0,05 составляет t_{уст 0,1} = 2,3τ; t_{уст 0,05} = 3τ.

Переходная характеристика выходного напряжения h_u2 по определению равна

Зная решение для интегрирующей цепи, можно сразу получить решение для дифференцирующей цепи и наоборот, поскольку u₁(t)=u_C+u_R. В частности, когда u₁(t)=E×1(t)

u_R =E-E(1-e^-t/t)=E e^-t/t.

Б). Пусть входной сигнал – одиночный прямоугольный импульс (рис. 5.12) амплитудой Е и длительностью t_и. Такой импульс представляет собой суперпозицию двух ступенчатых сигналов и записывается как

.

Зная отклик на ступенчатый сигнал и используя принцип суперпозиции, можно записать аналитическое выражение для выходного сигнала:

.

На рис 5.13 показаны три временные диаграммы выходного сигнала при различных соотношения между τ и t_и.

u1

t

–E

E

а

t<< tи

tи

u2

–E

E

t ~ tи

tи

u2

u1

t

б

E

в

tи

u2

u1

t

t >>tи

–E

E

tи

u1

t

Рис. 5.12 Рис. 5.13

В зависимости от соотношения между τ и t_и эта схема имеет три названия.

Если τ << t_и, то цепь называется дифференцирующей RC-цепью (рис. 5.13 а).

Если τ ≈ t_и, то цепь называется укорачивающей RC-цепью (рис. 5.13б).

Если τ >> t_и, то цепь называется разделительной RC-цепью (рис. 5.13 в).

Рассмотрим процессы, протекающие в цепи при воздействии на вход прямоугольного импульса при нулевых начальных условиях u_c(–0) = 0.

Напряжения на элементах связаны вторым законом Кирхгофа: u₁ = u_c + u_R.

При t < 0 u₁ = 0, u_С = 0, следовательно, u_R = 0. Это исходное состояние.

При t = +0 u₁ = Е, u_С = 0, E = 0 + u_R. Следовательно, u_R = Е.

При t > 0 E = u_c + u_R. Происходит заряд конденсатора.

С током i_зар заряда напряжение на нем возрастает, а на резисторе (на выходе) убывает от Е к нулю.

При t = t_и–0 E = u_C(tи)_,+ u_R(tи)_,. К моменту окончания импульса u_С = u_С(tи)_, u_R = Е – u_С(tи).

При t > t_и+0 u₁ = 0 = u_c + u_R.. Следовательно, u_R = –u_c. Поэтому знак выходного напряжения меняется на противоположный.

u1(t) u2(t) R L i(t)

Рис. 5.14

При t > t_и u₁ = 0 , u_R = –u_c. Происходит разряд конденсатора С током i_разр разряда, напряжение на нем убывает, убывает и напряжение на резисторе (на выходе) от –u_c(tи) к нулю.

Цепь, состоящая из RL-элементов (рис5.14), выполняет аналогичные преобразования над входными сигналами и называется дифференцирующей RL-цепью.

5.5. Расчет переходных характеристик последовательного
колебательного контура

Схема последовательного колебательного контура приведена на рис. 5.15 а.

Для расчета переходной характеристики установим связь между выходным u₂ и входным u₁ напряжениями. Входной сигнал имеет вид ступенчатого напряжения , тогда переходная характеристика h(t) находится из выражения h(t) = u₂(t)/E, где u₂(t) – выходное напряжение.

u2(t) u2(¥) = E u2(0) = 0 в i(0) = 0 C L R E R C L E L C R а u1(t) б
Рис. 5.15

Задачу будем решать классическим способом. За переменную в составляемом уравнении выбираем переменную, характеризующую энергетическое состояние цепи и наиболее просто связанную с выходным сигналом. Такой переменной является напряжение на конденсаторе u_С(t) = u₂(t).

1) Составим дифференциальное уравнение относительно переменной состояния цепи и приведем его к стандартному виду.

Данная цепь представляет контур, а потому, используя второй закон Кирхгофа и соотношения между напряжениями и токами на элементах схемы, запишем:

;
, .

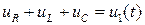Отсюда ; .

Подставим полученные напряжения в первое выражение:

.

Поделим на LC и введем обозначения .

Получим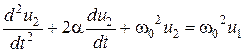

2) Запишем общее решение:

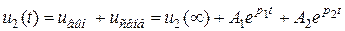
3) Найдем вынужденную составляющую общего решения .

Для этого составим схему замещения исходной цепи при t ® ∞, соответствующую (рис. 5.15 б), из которой и получим

=E

4) Найдем коэффициенты показателей экспоненты р₁ и p₂, которые являются корнями характеристического уравнения:

.

Отсюда .

5) Найдем постоянные интегрирования А₁, А₂ из начальных условий, т.е. при t = +0 для искомой функции, и ее производной согласно схеме в момент после коммутации (при t = +0, ω® ∞), которая приведена на рис. 5.15 в.

Составим систему:

;
,

или, в матричной форме: , – из решения которой и находим А₁ и А₂: .

6) Анализ корней и запись окончательного решения:

а) если , то корни – отрицательные действительные числа. Тогда

,

И окончательное решение записывается так:

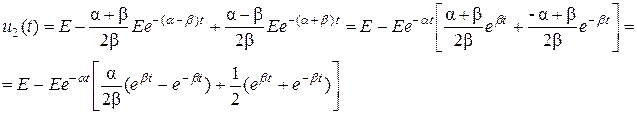Учитывая, что ; , а также, что при βt ® 0, , окончательно получим:

.

Такое решение называется апериодическим (рис. 5.16).

u2 t a > w0 E

Рис. 5.16

б) если , то корни 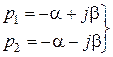комплексно сопряженные числа. В полученном решении нужно вместо b подставить мнимое число jb. Тогда, если учесть, что

; ,

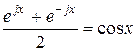то при α << β, получим следующее (рис. 5.17):

t e–at b = Öw02–a2 E

Рис. 5.17

.

Здесь ω₀ = (LC)^–1 – собственная частота колебательного контура; β = (ω₀² – α²)^1/2 – частота собственных колебаний в контуре при наличии резистивных потерь; α = R/(2L) – скорость затухания собственных колебаний в контуре, α =1/τ, где τ = 2L/R – постоянная времени контура.

 

5.6. Спектральный метод анализа переходных процессов

Спектральный метод применяется в тех случаях, когда входной сигнал может быть представлен спектром. Сигнал имеет спектр, когда он обладает конечной энергией, т.е. удовлетворяет условию: .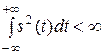

Этапы применения метода (рис.5.18):

1) по известному сигналу находится его спектр:

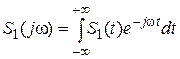– прямое преобразование Фурье;

2) по известной схеме электрической цепи определяется частотная функция цепи (частотная передаточная характеристика):

;

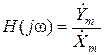
3) находится спектральная плотность выходного сигнала:

;

4) по известному спектру выходного сигнала находится сам выходной сигнал обратным преобразованием Фурье:

.