 |
|
Геометрическое определение вероятности
Геометрическое определение вероятности обобщает классическое на случай бесконечного множества элементарных исходов  . Пусть
. Пусть  представляет собой множество в пространстве
представляет собой множество в пространстве 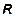 (числовая прямая),
(числовая прямая),  (плоскость),
(плоскость),  (
( 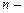 мерное евклидово пространство).
мерное евклидово пространство).
В пространстве 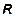 в качестве множеств будем рассматривать только промежутки и их объединения, т.е. множества, имеющие длину; в пространстве
в качестве множеств будем рассматривать только промежутки и их объединения, т.е. множества, имеющие длину; в пространстве  - те множества, которые имеют площадь; в
- те множества, которые имеют площадь; в  - множества, имеющие объём; в
- множества, имеющие объём; в  ,
,  , - множества, имеющие обобщённый (
, - множества, имеющие обобщённый ( 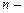 мерный) объём. Такие множества будем называть измеримыми.
мерный) объём. Такие множества будем называть измеримыми.
Под мерой  множества
множества  будем понимать длину, площадь, объём или обобщённый объём в зависимости от
будем понимать длину, площадь, объём или обобщённый объём в зависимости от  .
.
Будем считать, что пространство элементарных исходов случайного опыта  имеет конечную меру и точки
имеет конечную меру и точки  (элементарные исходы) в этом опыте выбираются так, что вероятность попадания
(элементарные исходы) в этом опыте выбираются так, что вероятность попадания  в любое измеримое множество
в любое измеримое множество  пропорциональна
пропорциональна 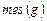 и не зависит от формы
и не зависит от формы  и расположения
и расположения  в пространстве
в пространстве  (последнее условие аналогично требованию о равновозможности элементарных исходов в классической схеме). Такой опыт называют геометрической схемой.
(последнее условие аналогично требованию о равновозможности элементарных исходов в классической схеме). Такой опыт называют геометрической схемой.
Итак, пусть случайный опыт представляет собой геометрическую схему и событие  есть измеримое подмножество пространства
есть измеримое подмножество пространства  . Тогда вероятностью события
. Тогда вероятностью события  называют число
называют число
 . (1.4.1)
. (1.4.1)
Это определение называют геометрическим определением вероятности, а вероятность (1.4.1) – геометрической вероятностью.
Легко убедиться в том, что геометрическая вероятность обладает теми же основными свойствами, что и классическая вероятность:
1.  для любого события
для любого события  .
.
2.  .
.
3.  для любых несовместных событий (
для любых несовместных событий ( 
 ).
).
Пример 1.4.1.
Точное значение физической величины округляют до ближайшего целого числа. Найти вероятность того, что абсолютная величина ошибки округления не превысит 0,1 (событие  ).
).
◄При округлении точного значения до ближайшего целого возникает случайная ошибка  , величина которой лежит в диапазоне от –0,5 до +0,5. Таким образом, опыт состоит в случайном выборе числа
, величина которой лежит в диапазоне от –0,5 до +0,5. Таким образом, опыт состоит в случайном выборе числа  из этого диапазона, соответствующий элементарный исход
из этого диапазона, соответствующий элементарный исход  . Поэтому пространство элементарных исходов
. Поэтому пространство элементарных исходов 
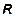 .
.
Событие  , согласно условию задачи, это множество
, согласно условию задачи, это множество  .
.











Рис. 1.4.1. К примеру 1.4.1.
Пространство  и множество
и множество  показаны на рис. 1.4.1. В данном случае мерой множества является его длина, поэтому
показаны на рис. 1.4.1. В данном случае мерой множества является его длина, поэтому  .►
.►
Пример 1.4.2.
К причалу для высадки пассажиров в течение ближайшего часа в случайные моменты времени должны подойти два катера. Одновременное причаливание обоих катеров невозможно. Время высадки пассажиров с первого катера составляет 10 мин, а со второго катера – 20 мин.
Найти вероятность того, что одному из катеров придётся ожидать освобождения причала (событие  ).
).
◄Обозначим время прихода первого катера через  , а второго – через
, а второго – через  . Тогда опыт можно представить как случайный выбор упорядоченной пары чисел
. Тогда опыт можно представить как случайный выбор упорядоченной пары чисел  , т.е. элементарными исходами
, т.е. элементарными исходами  являются точки пространства
являются точки пространства  (плоскости). Если выбрать в качестве единицы измерения времени 1 мин, то пространством элементарных исходов будет множество
(плоскости). Если выбрать в качестве единицы измерения времени 1 мин, то пространством элементарных исходов будет множество 
 . Очевидно, это квадрат со стороной 60 (рис. 1.4.2).
. Очевидно, это квадрат со стороной 60 (рис. 1.4.2).









 |




Рис. 1.4.2. К примеру 1.4.2
Событие  произойдёт в любом из следующих случаев:
произойдёт в любом из следующих случаев:
а) первый катер прибудет не позднее второго (  ) и при этом к моменту прихода второго катера высадка с первого катера ещё не закончится (
) и при этом к моменту прихода второго катера высадка с первого катера ещё не закончится (  ), т.е. если
), т.е. если  ;
;
б) второй катер придёт раньше, т.е.  и к прибытию первого катера высадка пассажиров на втором ещё не закончится:
и к прибытию первого катера высадка пассажиров на втором ещё не закончится:  , т.е. если
, т.е. если  .
.
Таким образом, условие появления события  описывается соотношениями
описывается соотношениями  , поэтому
, поэтому  . Область
. Область  на рис 1.4.2 заштрихована.
на рис 1.4.2 заштрихована.
В данном случае мера множества – это площадь. Площадь области  на рис. 1.4.2 равна площади квадрата без двух угловых треугольников поэтому
на рис. 1.4.2 равна площади квадрата без двух угловых треугольников поэтому  ,
,  и
и  .►
.►
Пример 1.4.3.
По дороге в институт студент едет последовательно на трёх автобусах разных маршрутов. Интервалы движения автобусов на этих маршрутах совпадают и равны  мин.
мин.
С какой вероятностью общее время, израсходованное студентом на ожидание автобусов, не превзойдёт  мин (событие
мин (событие  )?
)?
◄Обозначим  время ожидания первого автобуса,
время ожидания первого автобуса,  - время ожидания второго автобуса и
- время ожидания второго автобуса и  - время ожидания третьего автобуса.
- время ожидания третьего автобуса.




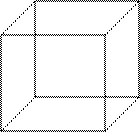


 |




Рис. 1.4.3. К примеру 1.4.3
Опыт состоит в случайном выборе чисел  ,
,  и
и  , т.е. упорядоченной тройки чисел
, т.е. упорядоченной тройки чисел  . Таким образом, элементарными исходами
. Таким образом, элементарными исходами  данного опыта являются точки пространства
данного опыта являются точки пространства  .
.
По условию задачи пространство элементарных исходов определяется так:  . Это куб с ребром
. Это куб с ребром  , см. рис. 1.4.3. Событие
, см. рис. 1.4.3. Событие  происходит, если
происходит, если  . Поэтому
. Поэтому  .
.
Точки, принадлежащие множеству  , лежат по ту же сторону от плоскости
, лежат по ту же сторону от плоскости  , что и начало координат (часть этой плоскости, расположенная внутри куба
, что и начало координат (часть этой плоскости, расположенная внутри куба  , заштрихована на рис. 1.4.3). Кроме того, точки множества
, заштрихована на рис. 1.4.3). Кроме того, точки множества  расположены в кубе
расположены в кубе  . Поэтому
. Поэтому  - это четырёхгранная пирамида, три грани которой лежат в координатных плоскостях, а четвёртая - в плоскости
- это четырёхгранная пирамида, три грани которой лежат в координатных плоскостях, а четвёртая - в плоскости  , см. рис. 1.4.3.
, см. рис. 1.4.3.
Меры множеств  и
и  - это их объёмы, поэтому
- это их объёмы, поэтому  ,
,  . Окончательно,
. Окончательно,  .►
.►
Замечание
В примерах 1.4.1 – 1.4.3 рассмотрены случайные опыты, сводящиеся к геометрической схеме в пространствах  ,
,  . Из решений этих примеров видно, что при использовании геометрического подхода вероятность события находится в результате выполнения следующих действий.
. Из решений этих примеров видно, что при использовании геометрического подхода вероятность события находится в результате выполнения следующих действий.
1. Определение размерности  пространства
пространства  данной геометрической схемы.
данной геометрической схемы.
2. Аналитическое описание пространства элементарных исходов  и подмножества
и подмножества  (с помощью неравенств, включений множеств и т.п.).
(с помощью неравенств, включений множеств и т.п.).
3. Геометрическое описание  и
и  (изображение областей
(изображение областей  и
и  ). Если
). Если  , геометрическое описание невозможно. При
, геометрическое описание невозможно. При  часто обходятся без геометрической иллюстрации в силу простоты задачи.
часто обходятся без геометрической иллюстрации в силу простоты задачи.
4. Вычисление  ,
,  и нахождение вероятности
и нахождение вероятности  по формуле (1.4.1). При
по формуле (1.4.1). При  обобщённый (
обобщённый (  -мерный) объём области
-мерный) объём области 
 находят с помощью
находят с помощью  -кратного интегрирования:
-кратного интегрирования:  .
.
Впервые геометрический подход к вычислению вероятности применил известный учёный Жорж Бюффон. В работе, написанной в 1733 году, он рассмотрел следующую задачу.
Пример 1.4.4. Задача Бюффона.
На плоскость, разграниченную параллельными прямыми, отстоящими друг от друга на расстояние  , наудачу бросается игла диной
, наудачу бросается игла диной 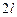 (
(  ). Найти вероятность события
). Найти вероятность события  {игла пересечет какую-либо из прямых }.
{игла пересечет какую-либо из прямых }.
◄Будем описывать положение иглы двумя координатами: углом  между иглой и прямыми и расстоянием
между иглой и прямыми и расстоянием  от центра иглы до ближайшей прямой, см рис. 1.4.4.
от центра иглы до ближайшей прямой, см рис. 1.4.4.












Рис. 1.4.4. К примеру 1.4.4
Тогда опыт можно представить как случайный выбор упорядоченной пары чисел  , т.е. элементарными исходами
, т.е. элементарными исходами  являются точки пространства
являются точки пространства  .
.
Пространство элементарных исходов  (прямоугольник), событие
(прямоугольник), событие  (криволинейная трапеция), см рис. 1.4.5.
(криволинейная трапеция), см рис. 1.4.5.






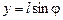
 |






Рис. 1.4.5. К примеру 1.4.4
Очевидно,  ,
,  , поэтому
, поэтому  .►
.►
Контрольные вопросы
1. Какой случайный опыт называют геометрической схемой?
2. Какое условие геометрической схемы аналогично требованию равновозможности элементарных исходов в классической схеме?
3. Приведите определение геометрической вероятности.
4. Какими основными свойствами обладает геометрическая вероятность?
5. Перечислите основные шаги нахождения вероятности в геометрической схеме.