|
|
Список алгоритмов рисования отрезков
Диаграмма Вороного

Диаграмма Вороного случайного множества точек на плоскости
Диаграмма Вороного конечного множества точек S на плоскости представляет такое разбиение плоскости, при котором каждая область этого разбиения образует множество точек, более близких к одному из элементов множества S, чем к любому другому элементу множества.
Алгоритм Чана (Тимоти М. Чан, 1996) — алгоритм построения выпуклой оболочки конечного множества точек на плоскости. Является комбинацией двух более медленных алгоритмов (сканирование по Грэхему O(nlogn) и заворачивание по Джарвису O(nh)). Недостатком сканирования по Грэхему является необходимость сортировки всех точек по полярному углу, что занимает достаточно много времени O(nlogn). Заворачивание по Джарвису требует перебора всех точек для каждой из h точек выпуклой оболочки, что в худшем случае занимает O(n2).
Алгоритм Грэхема — алгоритм построения выпуклой оболочки в двухмерном пространстве. В этом алгоритме задача о выпуклой оболочке решается с помощью стека, сформированного из точек-кандидатов. Все точки входного множества заносятся в стек, а потом точки, не являющиеся вершинами выпуклой оболочки, со временем удаляются из него. По завершении работы алгоритма в стеке остаются только вершины оболочки в порядке их обхода против часовой стрелки.
Алгоритм DDA-линии растеризует отрезок прямой между двумя заданными точками, используя вычисления с вещественными числами. Аббревиатура DDA в названии этого алгоритма машинной графики происходит от англ. Digital Differential Analyzer (цифровой дифференциальный анализатор) — вычислительное устройство, применявшееся ранее для генерации векторов...
Алгоритм
Пусть отрезок задан вещественными координатами концов (x1,y1); (x2,y2). Растровыми (целочисленными) координатами концевых точек становятся округлённые значения исходных координат: xstart = round(x1), ystart = round(y1); xend = round(x2), yend = round(y2).
Большее из двух чисел — (xend − xstart) или (yend − ystart) — по абсолютной величине принимается за количество шагов L цикла растеризации, увеличенное на 1.
В начале цикла вспомогательным вещественным переменным x и y присваиваются исходные координаты начала отрезка: x = x1; y = y1. На каждом шаге цикла эти вещественные переменные получают приращения (xend − xstart) / L; (yend − ystart) / L. Растровые же координаты, продуцируемые на каждом шаге, являются результатом округления соответствующих вещественных значений x и y.
Применение вычислений с вещественными числами и лишь однократное использование округления для окончательного получения значения растровой координаты обусловливают высокую точность и низкое быстродействие алгоритма.
Далее представлен программный код реализации алгоритма DDA-линии. Значения вспомогательных переменных x и y здесь сохраняются в виде массивов.
void dda_line (float x1, float y1, float x2, float y2){ int i, L, xstart, ystart, xend, yend; float dX, dY, x[1000], y[1000]; xstart = roundf(x1); ystart = roundf(y1); xend = roundf(x2); yend = roundf(y2); L = max(abs(xend-xstart), abs(yend-ystart)); dX = (x2-x1) / L; dY = (y2-y1) / L; i = 0; x[i] = x1; y[i] = y1; i++; while (i < L) { x[i] = x[i-1] + dX; y[i] = y[i-1] + dY; i++; } x[i] = x2; y[i] = y2;/* Output: -----------------------*/ i = 0; while (i <= L) { plot (roundf(x[i]), roundf(y[i])); /* Draws a point. */ i++; }/* -------------------------------*/Модифицированный алгоритм DDA-линии применяется для растеризации окружностей.
Marching cubes (англ. движущиеся кубики) — алгоритм в компьютерной графике, впервые предложенный в 1987 году Вильямом Лоренсеном (англ. William E. Lorensen) и Харви Клайном (англ. Harvey E. Cline), для обработки полигональной сетки изоповерхности трехмерного скалярного поля (чаще называемой сеткой вокселей - Voxel — образовано из слов: объёмный (англ. volumetric) и пиксел (англ. pixel) ).

Аналогичный алгоритм на плоскости называется marching squares.
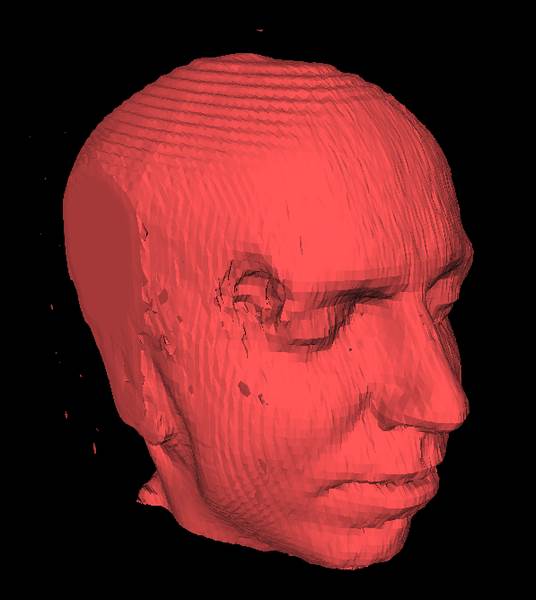

Принцип работы
Алгоритм пробегает скалярное поле, на каждой итерации просматривает 8 соседних позиций (вершины куба, параллельного осям координат) и определяет полигоны, необходимые для представления части изоповерхности, проходящей через данный куб. Далее на экран выводятся полигоны, образующие заданную изоповерхность.
Так как алгоритм выбирает полигоны, исходя только из положения вершин куба относительно изоповерхности, всего получается 256 (28 = 256) возможных конфигураций полигонов, которые можно вычислить заранее и сохранить в массиве. Поэтому каждый куб можно представить восьмибитным числом, сопоставив каждой вершине 1, если значение поля в точке больше, чем на изоповерхности, и 0 в противном случае. Полученное число используется в качестве индекса элемента массива, хранящего конфигурации полигонов. Наконец каждая вершина сгенерированного полигона помещается в подходящую позицию на том ребре куба, на котором она лежала изначально. Позиция вычисляется путем линейной интерполяции значений скалярного поля в концах ребра.
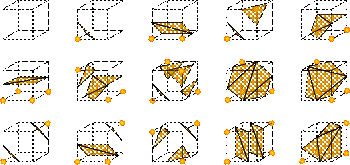
15 различных конфигураций куба
Заранее вычисленный массив из 256 конфигураций полигонов можно получить поворотами и отражениями 15 различных конфигураций куба. Однако использование всего 15 базовых конфигураций не гарантирует получение замкнутой поверхности.
Градиент скалярного поля в каждой точке сетки также является нормальным вектором предполагаемой изоповерхности, проходящей через эту точку. Поэтому возможно интерполировать эти нормали вдоль ребер каждого куба, чтобы найти нормали сгенерированных вершин, для корректного отображения модели при использовании освещения.
Данный алгоритм широко используется в медицине, например, в компьютерной и магнитно-резонансной томографии, а также для 3D моделирования метасфер или других метаповерхностей.
Marching squares (движущиеся квадраты)

Схематическое изображение алгоритма: цвет квадрата обозначает значение в данной клетке регулярной сетки, чем темнее - тем значение ближе к изолиниям. Красным показаны полученные изолинии.
Marching Squares (англ. движущиеся квадраты) – алгоритм в компьютерной графике, который генерирует изолинии на двухмерном скалярном поле.
Применение
Алгоритм используется при визуализации изобар на картах погоды и горизонталей на географических картах. Является упрощением алгоритма marching cubes для плоского случая.
Принцип работы
На вход алгоритм получает регулярную сетку, в каждом узле которой известно значение поля. Выходная сетка (на рисунке обозначена синим цветом) может иметь меньшее разрешение (в этом случае теряется точность, но уменьшается ступенчатость). Далее для каждого узла выходной сетки проверяется, выше ли значение в нем, чем на изоповерхности. Всем узлам, которые выше, приписывается "+", остальным "–". Далее рассматриваются квадратики выходной сетки, вершины которых лежат в отмеченных узлах. Всего получается 16 различных случаев, которые с учетом симметрий и поворотов можно свести к четырем:
- Случай 1: все вершины имеют один знак
- Случай 2: у одной вершины знак отличается
- Случай 3: вершины с одинаковыми знаками имеют общее ребро
- Случай 4: вершины с одинаковыми знаками не имеют общего ребра
В четвертом случае невозможно однозначно определить форму сегмента изолинии, поэтому дополнительно просматривается значение в центре квадрата (если входные данные это позволяют). При невозможности узнать значение в центре квадрата принятое решение может повлиять на связность изолинии.
Случай 1: все вершины находятся выше (или ниже) изоповерхности.
Случай 2: за исключением одной, все вершины находятся выше (или ниже) изоповерхности.
Случай 3: две вершины на одном ребре находятся выше (или ниже) изоповерхности.
Случай 4: две вершины, не имеющие общего ребра, находятся выше (или ниже) изоповерхности.
Решение Случая 4 при положительном значении в ячейке.
Решение Случая 4 при отрицательном значении в ячейке.
Для улучшения качества получаемой изолинии применяется линейная интерполяция. В таком случае конец сегмента изолинии на ребре квадрата делит ребро в отношении  , где f1,f2 - значения на концах ребра квадрата, c - значение изолинии. Фактически, конец сегмента изолинии "подтягивается" к тому концу ребра, который ближе к реальной изолинии.
, где f1,f2 - значения на концах ребра квадрата, c - значение изолинии. Фактически, конец сегмента изолинии "подтягивается" к тому концу ребра, который ближе к реальной изолинии.
Алгоритм Бентли — Оттмана (1979) позволяет найти все точки пересечений прямолинейных отрезков на плоскости. В нем применяется метод выметающей прямой (заметающей прямой, движущейся прямой, сканирующей линии; англ. sweeping line). В методе используется вертикальная выметающая прямая движущаяся слева направо, при этом отрезки, которые она пересекает при данной координате x, можно упорядочить по координате y, тем самым их можно сравнивать между собой (какой выше, какой ниже). Это сравнение можно осуществить, например, используя уравнение прямой, проходящей через две точки (отрезки заданы двумя своими конечными точками):  , где x1, y1 и x2, y2 — координаты, соответственно, первой и второй точек отрезка. Выметающая прямая перемещается по так называемым точкам событиям (левым и правым концам отрезков, а также точкам пересечения отрезков). После точки пересечения отрезки следует менять местами, так как, например, самый верхний из пересекающихся отрезков после точки пересечения становится самым нижним. Приведенный ниже алгоритм не рассчитан на случай, когда два отрезка пересекаются больше, чем в одной точке.
, где x1, y1 и x2, y2 — координаты, соответственно, первой и второй точек отрезка. Выметающая прямая перемещается по так называемым точкам событиям (левым и правым концам отрезков, а также точкам пересечения отрезков). После точки пересечения отрезки следует менять местами, так как, например, самый верхний из пересекающихся отрезков после точки пересечения становится самым нижним. Приведенный ниже алгоритм не рассчитан на случай, когда два отрезка пересекаются больше, чем в одной точке.
NB Выметающую прямую можно также представить как горизонтальную, движущуюся сверху вниз по координате y, и сравнивать пересекающие ее отрезки по координате x.
Алгоритм Ву — это алгоритм разложения отрезка в растр со сглаживанием. Был предложен У Сяолинем (Xiaolin Wu, отсюда устоявшееся в русском языке название алгоритма) в статье, опубликованной журналом Computer Graphics в июле 1991 года. Алгоритм сочетает высококачественное устранение ступенчатости и скорость, близкую к скорости алгоритма Брезенхема без сглаживания.

Горизонтальные и вертикальные линии не требуют никакого сглаживания, поэтому их рисование выполняется отдельно. Для остальных линий алгоритм Ву проходит их вдоль основной оси, подбирая координаты по неосновной оси аналогично алгоритму Брезенхема. Отличие состоит в том, что в алгоритме Ву на каждом шаге устанавливается не одна, а две точки. Например, если основной осью является Х, то рассматриваются точки с координатами (х, у) и (х, у+1). В зависимости от величины ошибки, которая показывает как далеко ушли пиксели от идеальной линии по неосновной оси, распределяется интенсивность между этими двумя точками. Чем больше удалена точка от идеальной линии, тем меньше ее интенсивность. Значения интенсивности двух пикселей всегда дают в сумме единицу, то есть это интенсивность одного пикселя, в точности попавшего на идеальную линию. Такое распределение придаст линии одинаковую интенсивность на всем ее протяжении, создавая при этом иллюзию, что точки расположены вдоль линии не по две, а по одной.
Алгоритм Грэхема — алгоритм построения выпуклой оболочки в двухмерном пространстве. В этом алгоритме задача о выпуклой оболочке решается с помощью стека, сформированного из точек-кандидатов. Все точки входного множества заносятся в стек, а потом точки, не являющиеся вершинами выпуклой оболочки, со временем удаляются из него. По завершении работы алгоритма в стеке остаются только вершины оболочки в порядке их обхода против часовой стрелки.
Алгоритм
В качестве входных данных процедуры Graham выступает множество точек Q, где  . В ней вызывается функция Top(S), которая возвращает точку, находящуюся на вершине стека S, не изменяя при этом его содержимое. Кроме того, используется также функция NextToTop(S), которая возвращает точку, расположенную в стеке S, на одну позицию ниже от верхней точки; стек S при этом не изменяется.
. В ней вызывается функция Top(S), которая возвращает точку, находящуюся на вершине стека S, не изменяя при этом его содержимое. Кроме того, используется также функция NextToTop(S), которая возвращает точку, расположенную в стеке S, на одну позицию ниже от верхней точки; стек S при этом не изменяется.
 — остальные точки множества Q, отсортированные в порядке возрастания полярного угла, измеряемого против часовой стрелки относительно точки p0 (если полярные углы нескольких точек совпадают, то по расстоянию до точки p0)3) Push(p0,S)4) Push(p1,S)5) for i = 2 to m do6) while угол, образованный точками NextToTop(S),Top(S) и pi, образуют не левый поворот (при движении по ломаной, образованной этими точками, мы движемся прямо или вправо)7) do Pop(S)8) Push(pi,S)9) return S
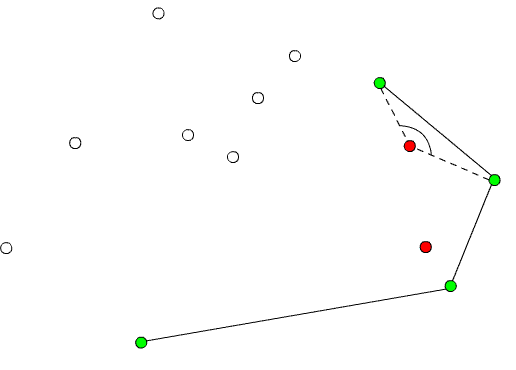
— остальные точки множества Q, отсортированные в порядке возрастания полярного угла, измеряемого против часовой стрелки относительно точки p0 (если полярные углы нескольких точек совпадают, то по расстоянию до точки p0)3) Push(p0,S)4) Push(p1,S)5) for i = 2 to m do6) while угол, образованный точками NextToTop(S),Top(S) и pi, образуют не левый поворот (при движении по ломаной, образованной этими точками, мы движемся прямо или вправо)7) do Pop(S)8) Push(pi,S)9) return S Для определения, образуют ли три точки a, b и c левый поворот, можно использовать обобщение векторного произведения на двумерное пространство, а именно условие левого поворота будет выглядеть следующим образом: uxvy − uyvx > 0, где 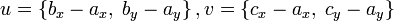
Алгоритмы построения отрезка — графические алгоритмы аппроксимации отрезка на дискретном графическом устройстве (растеризации), например, мониторе или принтере.
Стандартными требованиями к алгоритмам являются скорость работы, равномерная яркость и прямой вид полученных отрезков, совпадение начальных и конечных координат полученной и идеальной линии. Для дискретного устройства данные требования зачастую невыполнимы. Отрезок нельзя провести из одной точки в другую однозначно (кроме горизонтальных, вертикальных и наклонённых под углом 45° отрезков), начало и конец отрезка имеют координаты ближайших к ним пикселов, расстояние между пикселами диагональных отрезков больше, чем между пикселами вертикальных и горизонтальных.

Список алгоритмов рисования отрезков
- Алгоритм DDA-линии — простой алгоритм, использующий вещественную арифметику.
- Алгоритм Брезенхэма — оптимизированный алгоритм, использующий целочисленную арифметику и только операции сложения и вычитания.
- Алгоритм Ву — модифицированный алгоритм Брезенхэма, обеспечивающий сглаживание.