Главная | Обратная связь

ПЕРЕХОДНЫХ ПРОЦЕССОВ В РУ АЭС С ВВЭР

В. М. ЗЕНОВ

 

ВВЕДЕНИЕ В МОДЕЛИРОВАНИЕ И АНАЛИЗ

ПЕРЕХОДНЫХ ПРОЦЕССОВ В РУ АЭС С ВВЭР

 

Севастополь

 

 

 

Аннотация

Учебное пособие предназначено для самостоятельной работы студентов специальности «Атомная энергетика» с материалом раздела «Основы моделирования реакторных установок АЭС» учебной дисциплины «Нестационарные процессы и управление ЯЭУ».

Обсуждаются принципы построения теплогидравлических моделей энергетического оборудования реакторных установок АЭС на примере типовой РУ В-320 энергоблока с ВВЭР-1000. Для отдельных элементов энергоустановки рассматриваются дифференциальные уравнения сохранения с необходимыми замыкающими соотношениями. Описан алгоритм применения разработанной модели на основе численного метода интегрирования Эйлера. Приведены примеры выполнения анализа переходных процессов в РУ с ВВЭР на основе численных экспериментов на модели.

 

СОДЕРЖАНИЕ

 

1. Введение.

2. Основные законы и уравнения сохранения.

3. Замыкающие соотношения для систем уравнений.

4. Модели оборудования реакторной установки.

5. Особенности реализации моделей энергооборудования.

6. Анализ некоторых результатов моделирования.

7. Заключение.

8. Перечень ссылок

9. Перечень сокращений

 

1. Введение

 

Специалистам занятым эксплуатацией ядерных энергетических установок атомных электростанций в своей деятельности приходится регулярно встречаться с контролем и управлением переходными процессами в системах и оборудовании ЯЭУ. Учитывая большие единичные мощности энергоблоков АЭС, их существенное влияние на устойчивость энергосистемы Украины вполне понятны требования руководства АЭС и энергетической отрасли к обеспечению высокой квалификации оперативного персонала блочных щитов управления энергоблоками, реакторного и турбинного цехов станции для безопасного и надежного функционирования АЭС.

Нестационарные режимы работы ЯЭУ не могут проводиться на действующих энергоблоках для обучения персонала АЭС ввиду дороговизны подобных экспериментов и по условиям обеспечения безопасности станции. Поэтому детальное изучение особенностей переходных процессов в энергетическом оборудовании ЯЭУ АЭС, отработка практических действий персонала по изменению режимных состояний энергоблоков должны выполняться преимущественно на тренажерах и имитаторах такого оборудования полномасштабного или локального типа.

Применение различных тренажеров ЯЭУ АЭС уже стало повседневной практикой отработки навыков оперативного персонала по обычному и противоаварийному управлению ЯЭУ на всех АЭС Украины. Знание основ анализа переходных процессов, способов моделирования и прогнозирования поведения ЯЭУ стало на АЭС базой реальной профессиональной деятельности и оперативного персонала, и персонала подразделений инженерной поддержки процесса эксплуатации.

В подобных обстоятельствах актуальным направлением подготовки и повышения квалификации специалистов АЭС является изучение особенностей переходных процессов в ЯЭУ, приобретение навыков по анализу текущего состояния основного оборудования ЯЭУ, прогнозированию его поведения при различных оперативных переключениях, отказах оборудования и аварийных ситуациях на базе специализированных высших учебных заведений, таких как Севастопольский НИЯЭиП.

 

 

2. Основные законы и уравнения сохранения.

 

2.1 Особенности подходов к описанию уравнений сохранения

Описание теплогидравлических процессов в оборудовании АЭС во многом схоже с описанием процессов в газовой динамике. Такая схожесть, конечно, не случайна, так как связана с подобием описываемых сплошных сред, каковыми являются одно- и двухфазные жидкости, широко применяемые в качестве теплоносителей и рабочих тел в теплоэнергетике. Исторически сложилось так, что именно в газовой динамике ранее, чем в остальных областях техники, был развит мощный математический аппарат для конструирования сложных моделей потоков, режимов обтекания, исследования температурных полей и т.д. Поэтому бурное развитие расчетно-аналитических методов в теплогидравлике часто основывалось ( и в настоящее время основывается) на уже апробированных подходах и методах, полученных в газовой динамике.

Уравнения газовой динамики - это математические выражения основных законов сохранения (массы, энергии, импульса). Исходные уравнения обычно записываются в виде дифференциальных уравнений в частных производных, учитывая непрерывность свойств рассматриваемой среды. Примером часто используемой системы уравнений сохранения может служить их форма, приведенная в [1]:

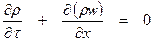, (2.1)

, (2.2)

, (2.3)

Однако, для получения практического результата физическое пространство аппроксимируют разностной сеткой, а исходные уравнения - их разностными аналогами. В этом случае для численного решения используют метод конечных разностей [2], дающий возможность описать поставленную задачу системой алгебраических уравнений, чаще нелинейных. Качество решения задачи во многом определяется способом связи переменных, так называемой разностной схемой решения, а также величиной шага разностной сетки: на мелких, "подробных" сетках разностные схемы работают лучше.

Вид и состав уравнений, конечно же, должен отражать основные качественные стороны изучаемого процесса или явления, но в то же время допускать относительно простое его математическое описание. В зависимости от поставленной задачи предварительно оцениваются ведущие, доминирующие факторы, благодаря которым оказывается главное влияние на ход процесса. В других случаях этот основной для данной задачи фактор может оказаться второстепенным и не играть столь важного значения. Этим подчеркивается мысль о том, что в различных случаях степень детализации описания задачи может быть разной, в зависимости от принятых упрощений и других постулируемых положений, называемых "допущениями модели". В качестве примера таких допущений можно привести следующие часто используемые положения:

· поток жидкости в контуре принимается одномерным (т.е. его основные параметры такие как давление, температура, скорость изменяются только вдоль одной координаты - оси канала, а в радиальном направлении - неизменны);

· отсутствует распространение тепла теплопроводностью вдоль оси кана- ла (т.е. теплообмен осуществляется только благодаря радиальному притоку тепла от стенок канала или перемешиванию сред, включая фазовые переходы: конденсацию или испарение);

· поток двухфазной жидкости в канале является гомогенным, равновесным (т.е. жидкость и пар в канале равномерно перемешаны, имеют одинаковую температуру и движутся с одинаковой скоростью);

· в каждом отдельно рассматриваемом элементе оборудования или участке циркуляционного контура используется "точечная" термодинамическая модель (т.е. все основные термодинамические параметры среды являются средневзвешенными для данного объема и условно связываются с геометрическим центром данного объема).

Кстати, последнее допущение является весьма распространенным в известных теплогидравлических кодах и моделях. В частности, коды RELAP5 [3], ATHLET (Германия), ТРАП (ОКБ Гидропресс, Россия) работают с так называемыми "многоэлементными" моделями, в которых любой агрегат или контур состоит из большого числа отдельных объемов-элементов, связанных между собой. При этом основные термодинамические параметры осредняются по каждому объему и "как бы стянуты в одну точку" - центр этого объема. По этой причине подобные теплогидравлические модели принято называть "точечными" моделями объекта. Понятно, что последовательное увеличение числа "объемов-элементов" при моделировании любого объекта приводит к измельчению самих "элементов". В этом случае все термодинамические параметры внутри них действительно будут очень близки друг другу в любой точке такого "элемента". Таким образом, при стремлении числа элементов моделирования к бесконечности можно перейти от "точечной" модели объекта к модели с распределенными параметрами, т.е. к точной модели, учитывающей все нюансы изменения состояния рабочих сред в реальном объекте. Однако, надо ясно осознавать, что такой переход требует и соответствующего увеличения объема самой модели, т.е. увеличения порядка системы уравнений, необходимой для описания элементов модели, вычислительных ресурсов компьютера (объема оперативной памяти, быстродействия процессора) для того, чтобы время решения задачи оставалось достаточно приемлемым. Поэтому в каждом конкретном случае следует искать некий оптимум, учитывающий и точность расчета, и сложность модели, и доступные ресурсы компьютера.

При использовании "точечных" теплогидравлических моделей надо учитывать и такое их важное достоинство, как доступность и относительная простота исходной системы уравнений, что значительно облегчает изучение принципов моделирования, понимание реальных возможностей модели, путей ее совершенствования и унификации. Дело в том, что в "точечных" моделях в каждом объеме-элементе используются средневзвешенные, или интегральные параметры, что позволяет относительно просто перейти от сложных (в записи и решении) дифференциальных уравнений сохранения в частных производных и "сеточных" методов решения, к обыкновенным дифференциальным уравнениям сохранения и относительно простым в программной реализации методам решения систем дифференциальных уравнений, например, методы Эйлера, Рунге-Кутта, Адамса-Башфорта и др. В какой-то мере, это делается в ущерб точности описания объекта, но как уже отмечено выше - необходимую точность можно обеспечить увеличением числа элементов разбиения объекта. Поэтому в данном пособии читатель встретится именно с этим упрощенным вариантом описания (модели-рования) объектов - их точечным приближением.

2.2 Общий вид уравнений сохранения в точечном приближении.

Для всех законов сохранения простейшей формой записи описывающих их уравнений являются алгебраические соотношения баланса потоков массы и энергии в любом элементе изучаемой системы. Например, в установившемся (стационарном) режиме можно написать равенство [4] между количеством массы вещества, поступившего в элемент (притоком) и вышедшего за его пределы (стоком) за тот же промежуток времени:

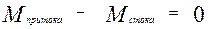, кг (2.4)

По аналогии с этим выражением может быть записано и уравнение баланса между количеством энергии, поступившим в элемент и покинувшим его за тот же промежуток времени:

, Дж (2.5)

При этом величина "стока" массы или энергии может включать в себя составляющую, по смыслу являющуюся каким-либо второстепенным потоком - потерями массы или энергии. Понятно, что "нулевая" правая часть выражений (1.1), (1.2) справедлива лишь для частного случая, стационарного режима. Для нестационарных процессов характерно нарушение баланса между "притоками" и "стоками" массы вещества и энергии, что приводит к увеличению или уменьшению количества вещества или его внутренней энергии и соответствующему изменению термодинамического состояния среды в рассматриваемом элементе. В этих условиях правая часть выражений (1.1), (1.2) будет иметь смысл приращений массы и энергии в элементе соответственно. Если отнести приращение указанных функций к приращению аргумента, выбрав в качестве аргумента время, устремив при этом приращение аргумента к нулю, то перейдем к производным указанных функций и дифференциальной форме записи обсуждаемых уравнений сохранения:

кг/с (2.6)

дж/с (Вт) (2.7)

При этом обозначения входящих в уравнения (1.3), (1.4) компонент взяты общепринятыми для данных физических величин в соответствии с их размерностями. Действительно, производная массы по времени имеет размерность массового расхода (кг/с), а производная энергии по времени - размерность мощности (Вт). Кроме того, форма записи уравнений (1.3), (1.4) считается общепринятой в математике и в инженерных расчетах для обыкновенных дифференциальных уравнений, при которой в левой части уравнения находится только производная, а правая часть уравнения является выражением для расчета этой производной. Поэтому именно с этим смыслом в теплогидравлических моделях обычно применяют подобные термины: "левая часть", "правая часть" дифуравнения...

Третьим важным уравнением, необходимым при описании динамических режимов в теплогидравлике является уравнение сохранения импульса, математическое выражение закона сохранения количества движения. Как известно, импульсом системы называют произведение массы системы на скорость ее центра инерции: P = M* v.

Размерность импульса - кг* м /с, а производнаяимпульса по времени

имеет размерность: кг* м /с² - произведения массы на ускорение, т.е. силы. Таким образом, уравнение сохранения импульса в дифференциальной форме характеризует баланс всех действующих сил в рассматриваемом элементе, включая как силы объемного действия (гравитация, потенциальная разность давлений), так и поверхностные (трение о стенку канала, межфазное трение и т.п.). В первом приближении можно записать уравнение сохранения импульса по аналогии с уравнениями (2.6), (2.7) в виде:

н (2.8)

где Р_ускор. - комплекс сил, способствующих ускорению потока вещества в изучаемом элементе, P_тормож - комплекс сил, способствующих торможению потока, н - ньютон - единица измерения силы в международной системе единиц СИ. В случае равенства ускоряющей и тормозящей составляющих величина импульса потока вещества в элементе - неизменна, что на практике означает постоянство скорости потока во времени. Уравнения (2.6-2.8) могут быть строго получены из уравнений (2.1-2.3) путем интегрирования последних по длине канала движущейся сплошной среды.

Набор уравнений (2.6), (2.7),(2.8) обычно используется при разработке теплогидравлических моделей оборудования и составляет основу математического описания любого элемента такого оборудования. В каждом конкретном случае правая часть указанных уравнений сохранения будет иметь свой уникальный вид, учитывающий особенности течения (гидродинамики) потока и теплообмена в элементе.

 

3. Замыкающие соотношения для систем уравнений.

 

Практически во всех случаях при разработке модели того или иного оборудования не удается получить решение системы уравнений (2.6-2.8) и получить искомый характер изменения основных термодинамических параметров среды в объекте без привлечения дополнительной информации. В нестационарном режиме многие важные параметры являются переменными величинами и, в свою очередь, влияют на интенсивность процесса, на общий характер поведения системы. Например, с изменением температуры происходит заметное изменение теплопроводности, теплоемкости, плотности и вязкости среды. Это приводит к изменению скорости потока, оказывает влияние на коэффициенты теплоотдачи, а в итоге и на величину тепловых потоков, т.е. мощности "притока" и "стока". Изменение скорости приводит и к существенным колебаниям гидравлических потерь (на общей шероховатости и на местных сопротивлениях), что, конечно же, отражается на распределении давлений в канале потока и, естественно, на величине расходов притока и стока среды. По сути дела, необходимость ввода дополнительной информации в вычислительный процесс обусловлена тем, что число переменных в имеемой системе уравнений больше числа уравнений. Как говорят в подобных случаях: "система уравнений является незамкнутой...". Таким образом, для "замыкания системы" и требуется введение дополнительных расчетных соотношений (как правило - алгебраических), которые называются "замыкающими соотношениями". Многие пользовались в теплогидравлических расчетах "Таблицами теплофизических величин для воды и водяного пара" [5], различного рода справочниками по гидравлике, конструкционным и теплоизоляционным материалам и т.п. Именно такого рода информация требуется на каждом шаге расчета нестационарного процесса с изменяющимися параметрами рабочей среды и температуры теплообменных поверхностей в элементе. Если речь идет о термодинамических функциях, то обычно говорят об "уравнениях состояния" для рабочей среды. Кстати, "Таблицы" [5] есть не что иное, как уравнения состояния воды и водяного пара, представленные в табличной форме. Очень важными для обсуждаемых расчетов являются корректно заданные в замыкающих соотношениях зависимости коэффициентов теплоотдачи для одно- и двухфазных потоков, коэффициенты гидравлических сопротивлений для различных режимов течения [6]. В некоторых случаях это могут быть и уравнения для определения высоты уровня жидкости в сосуде для последующего точного расчета величины парового объема и давления среды в этом элементе энергоустановки.

Способы задания замыкающих соотношений различны. Как уже отмечено выше, это могут быть обычные таблицы, для использования которых необходимо иметь два аргумента для однофазной среды (недогретая до насыщения жидкость, перегретый пар) или один аргумент для двухфазного состояния. Тогда в память компьютера необходимо будет внести соответствующие массивы данных, и после всякого обращения к таблицам в ходе расчетов отыскивать требуемые параметры (например энтальпии или теплоемкости), применяя, например, процедуру линейной интерполяции табличных данных. Иначе говоря, компьютер должен выполнять работу, которую пришлось бы сделать самому, выполняя расчет вручную.

Возможен иной вариант задания необходимых данных в модели: аппроксимация (приближенное описание) данных алгебраическими или тригонометрическими уравнениями. Наиболее простыми из них являются полиномы - алгебраические многочлены второго и более порядков вида:

,(3.1)

Обычно подобные полиномы получают аппроксимируя сложные зависимости методом наименьших квадратов. Методика аппроксимации довольно доступно описана во многих справочниках по численным методам в математике. Как правило, чем выше порядок полинома, тем более высокая точность аппроксимации может быть достигнута. Вместе с тем, следует быть очень внимательным к границам применимости подобных полиномов, поскольку при их использовании за рекомендованными пределами возможно получение совершенно нефизичных результатов, например отрицательных давлений или теплопроводностей. Расчет текущих термодинамических параметров в модели реакторной установки, которая легла в основу настоящего учебного пособия, программно реализован с помощью алгебраических полиномов.

Более громоздким и реже встречающимся методом аппроксимации является приближение функций тригонометрическими рядами Фурье вида:

(3.2)

Указанный метод также нашел достаточное отражение в литературе и при соответствующем числе членов ряда дает высокую точность аппроксимации, однако требует несколько больших затрат машинного времени на расчеты тригонометрических функций.

 

 

4. Модели оборудования реакторной установки.

 

4.1 Парогенератор реакторной установки.

Парогенератор является одним из важнейших элементов РУ АЭС, от нормальной работы которого зависит надежность отвода тепла, генерируемого в ядерном реакторе и температурный режим активной зоны ЯР. Для подавляющего большинства эксплуатационных режимов работы ПГ циркуляция теплоносителя 1-го контура обеспечивается главными циркуляционными насосами, характеристики которых достаточно стабильны, а создаваемые массовые расходы практически неизменны во времени. Это работа на номинальной мощности энергоблока, работа на пониженных уровнях мощности, включая режимы с неполным числом петель, это разогрев и расхолаживание РУ и т.п. В подобных случаях для 1-го контура характерно относительное постоянство распределения давлений по отдельным участкам, что позволяет принять упрощенный (в алгебраической, а не в дифференциальной форме) вариант учета сохранения импульса в модели РУ в целом. Наиболее важными при таком подходе остаются уравнения сохранения массы и энергии рабочей среды. Аналогичный подход применим и для описания теплогидравлических процессов в ПГ со стороны 2-го контура.

 

4.1.1 Сторона теплоносителя (1-го контура):

а) Уравнение сохранения массы теплоносителя

кг/с (4.1)

Здесь: - - массовый расход теплоносителя на входе в ПГ;

- - массовый расход теплоносителя на выходе из ПГ.

Часто в расчетах более удобным бывает использование не изменения массы среды М в элементе, а изменения ее удельного объема v (м³/кг), поскольку последний является термодинамическим параметром и может быть применен в уравнении состояния для поиска, например, температуры или давления среды. В этом случае в (4.1) вместо М подставляют отношение ( V / v ), где V (м³) - объем моделируемого элемента. Для нашего случая это объем, занимаемый теплоносителем в ПГ. Тогда после дифференцирования отношения ( V / v ) и несложных преобразований получим иной вид уравнения сохранения массы:

, м³/ (кг× с) (4.2)

б) Уравнение сохранения энергии теплоносителя

(кДж/с) (4.3)

Здесь: - - приток энергии с горячим теплоносителем в ПГ;

· - - сток энергии с охлажденным теплоносителем из ПГ;

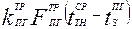· - - сток энергии теплопередачей от теплоносителя к

пароводяной смеси второго контура через трубчатку ПГ;

· - - энтальпия ТН на входе в парогенератор, кДж/кг;

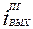· - - энтальпия ТН на выходе из парогенератора, кДж/кг;

· - - коэффициент теплопередачи от ТН к РТ, кВт/(м²·°С);

· - - поверхность теплообмена трубчатки ПГ, м²;

· - - средняя температура теплоносителя в ПГ, °С;

· - - температура насыщения рабочего тела в ПГ, °С.

Как и в случае с уравнением сохранения массы представленная форма уравнения сохранения энергии проста и доступна для понимания, однако не очень удобна для практических расчетов. Поэтому вместо энергии в обсуждаемое уравнение чаще подставляют произведение ( М × u ) массы среды на ее удельную внутреннюю энергию - u (кДж/кг), имеющее ту же размерность, что и (кДж). В итоге получают иной вид уравнения сохранения энергии, где в качестве интегрируемой переменной использована удельная внутренняя энергия, параметр среды:

кДж/ (кг× с)

(4.4)

4.1.2 Сторона рабочего тела (2-го контура):

а) Уравнение сохранения массы пароводяной смеси

кг/с (4.5)

Здесь: - - массовый расход ПВ на входе в ПГ;

· - - массовый расход насыщенного пара на выходе из ПГ;

· - - массовый расход продувки котловой воды из ПГ.

По аналогии с уравнением (4.2) представим уравнение сохранения массы пароводяной смеси 2-го контура в более удобной для расчетов форме:

, м³/ (кг× с) (4.6)

Здесь: - - удельный объем пароводяной смеси в ПГ;

- - объем ПГ по второму контуру.

б) Уравнение сохранения энергии пароводяной смеси

– (кВт) (4.7)

Здесь: - - приток энергии с ПВ в ПГ;

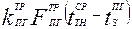· - - основной приток энергии теплопередачей от теплоносителя через поверхность теплообмена;

· - - сток энергии с насыщенным паром из ПГ;

· - - сток энергии с продувочной водой из ПГ;

· - - сток энергии теплопередачей от пароводяной

смеси второго контура к воздуху гермозоны (потери тепла);

· - - энтальпия ПВ на входе в парогенератор, кДж/кг;

· - - энтальпия насыщенной котловой воды, кДж/кг;

· - - энтальпия насыщенного пара на выходе из ПГ, кДж/кг;

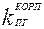· - - коэффициент теплопередачи от РТ к воздуху, кВт/(м²·°С);

· - - поверхность теплообмена корпуса ПГ, м²;

· - - температура насыщения рабочего тела в ПГ,°С;

· - - температура воздуха гермозоны в боксах ПГ,°С.

По аналогии с уравнением (4.4) представим уравнение сохранения энергии пароводяной смеси в полости 2-го контура ПГ в более удобном для расчетов виде:

кДж/ (кг× с) (4.8)

Здесь: - - удельная внутренняя энергия пароводяной смеси в ПГ;

- - объем ПГ по второму контуру.

 

4.1.3 Замыкающие соотношения

Как видно из уравнений (4.1- 4.8) переменными величинами, требующими самостоятельного определения, являются энтальпии теплоносителя на входе и на выходе из парогенератора и энтальпия питательной воды, коэффициенты теплопередачи от теплоносителя к рабочему телу и от рабочего тела к воздуху гермозоны, средняя температура теплоносителя в трубках ПГ и температура насыщения в полости 2-го контура. Энтальпии определяются из уравнений состояния вида , температура теплоносителя - из уравнения состояния , температура насыщения - из зависимости , коэффициенты теплопроводности, вязкости для однофазного теплоносителя - все с использованием алгебраических полиномов различных порядков, обеспечивающих точность расчета в пределах 0.3-1.0% . При этом для коэффициента теплопередачи принята упрощенная форма расчета, соответствующая выражению для теплообмена через плоскую стенку.

 

4.2 Паровой компенсатор давления РУ АЭС.

Компенсатор давления является дыхательной (расширительной) емкостью 1-го контура ЯЭУ и обеспечивает безопасное расширение и сжатие теплоносителя при изменении его средней температуры во всем диапазоне эксплуатационных параметров. Важным достоинством парового компенсатора давления в РУ с ВВЭР является возможность эффективного и плавного регулирования давления в 1-ом контуре, обеспечивая необходимый запас до насыщения по температуре на выходе из тепловыделяющих сборок реактора и бескавитационный режим работы главных циркуляционных насосов. Повышение давления в контуре осуществляется генерацией дополнительного пара в КД путем включения одной или нескольких групп встроенных трубчатых электронагревателей. Понижение давления до установленного уровня производится конденсацией части пара в паровой полости КД посредством впрыска относительно холодного теплоносителя с напора одного из ГЦН. Как и в случае с парогенератором, в модели КД применено упрощенное описание уравнения сохранения импульса, не требующее его записи и решения в дифференциальной форме. Поэтому основное внимание уделено уравнениям сохранения массы и энергии теплоносителя в КД.

4.2.1 Уравнения сохранения для ТН в КД

а) Уравнение сохранения массы теплоносителя

кг/с (4.9)

Здесь: - - массовый расход теплоносителя из горячей нитки петли 1-го контура по дыхательному трубопроводу в КД;

· - - массовый расход теплоносителя из КД по дыхательному трубопроводу в горячую нитку петли 1-го контура;

· - - массовый расход впрыска теплоносителя из холодной нитки петли 1-го контура в паровой объем КД;

· - - массовый расход сброса пара из парового объема КД через импульсно-предохранительный клапан в бак-барботер.

б) Уравнение сохранения энергии теплоносителя

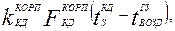(кВт) (4.10)

Здесь:

· - - приток энергии в КД с приходом ТН из 1-го контура;

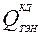· - - приток энергии в КД от трубчатых электронагревателей;

· - - приток энергии в КД от впрыска холодного ТН;

· - - сток энергии из КД с уходом ТН в 1-й контур

· - - сток энергии со сбросом пара из КД на бак-барботер;

· - - сток энергии теплопередачей от пароводяной

смеси в КД к воздуху гермозоны (потери тепла);

· - - энтальпия ТН на выходе из ЯР (горячий ТН), кДж/кг;

· - - энтальпия ТН на входе в ЯР (холодный ТН), кДж/кг;

· - - энтальпия насыщенной воды в КД, кДж/кг;

· - - энтальпия насыщенного пара в КД, кДж/кг;

· - - коэффициент теплопередачи от пароводяной смеси в КД к

воздуху гермозоны, кВт/(м²·°С);

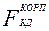· - - поверхность теплообмена корпуса КД, м²;

· - - температура насыщения ТН в КД,°С;

· - - температура воздуха гермозоны в боксе КД, °С.

4.2.2 Замыкающие соотношения

Как видно из уравнений (4.9- 4.10) переменными величинами, требующими самостоятельного определения, являются энтальпии теплоносителя на входе и на выходе из реактора, энтальпии воды и пара на линии насыщения, коэффициент теплопередачи от пароводяной смеси в КД к воздуху гермозоны и температура насыщения в полости КД. Энтальпии определяются из уравнений состояния вида , а для состояния насыщения - как функции давления; температура насыщения - из зависимости , коэффициенты теплопроводности, вязкости - все с использованием алгебраических полиномов различных порядков. Как и в модели ПГ для коэффициента теплопередачи в КД принята упрощенная форма расчета, соответствующая выражению для теплообмена через плоскую стенку, вполне приемлемая для сосуда с диаметром более 3-х метров.

4.3. Участок главного циркуляционного трубопровода.

Очень часто в практике моделирования используют уравнение сохранения энергии, содержащее в качестве интегрируемой функции температуру объекта моделирования. При этом объект может иметь различную природу: жидкость, газ, твердое тело. Общее выражение для такого уравнения легко получить, продифференцировав известное выражение для количества тепла принимаемого или отдаваемого телом в процессе теплообмена:

 

, кДж (4.11)

Здесь:

· - энергия, расходуемая на подогрев тела, кДж;

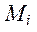· - масса тела, кг;

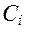· - теплоемкость тела, кДж/кг× град;

· - величина подогрева тела, °С.

После дифференцирования уравнение сохранения энергии примет вид:

= N_{притока} - N_стока, кдж/с(кВт) (4.12)

Полученное выражение является аналогом уравнения 2.7 (см. гл. 2). Воспользуемся им для записи уравнения сохранения энергии для металла участка трубопровода главного циркуляционного контура РУ АЭС:

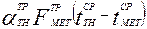= ( - ) /C_мет×M_мет, °С/с

Здесь: (4.13)

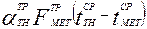· - - приток энергии теплоотдачей от теплоносителя к металлу через поверхность трубопровода;

· - - сток энергии теплоотдачей от металла

трубопровода к воздуху гермозоны (потери тепла);

· - - коэффициент теплоотдачи от ТН к металлу, кВт/(м²·°С);

· - - коэффициент теплоотдачи от металла к воздуху,

кВт/(м²·°С);

· - - поверхность теплообмена трубопровода, м²;

· - - средняя температура теплоносителя на участке трубо-

провода,°С;

· - - средняя температура металла участка трубопровода,°С;

· - - температура воздуха гермозоны в районе ГЦТ,°С.

В приведенном примере уравнения сохранения энергии для металла трубопровода комплекс С×М практически неизменен для любых режимов работы РУ АЭС. В случае применения уравнения сохранения энергии аналогично вида для потоков рабочих сред следует помнить, что и теплоемкость, и масса рабочей среды в моделируемом объеме - величины переменные и требуют регулярных уточнений (на каждом шаге интегрирования) перед их подстановкой в уравнение. Кроме того, нельзя забывать о том, что рассмотренный вид уравнения сохранения энергии нельзя использовать для расчета двухфазных потоков, поскольку каких-либо табличных или аналитических зависимостей для теплоемкости двухфазных смесей не существует.

 

5. Особенности реализации моделей энергооборудования.

 

Довольно часто начинающие исследователи испытывают трудности в первоначальном запуске созданной ими модели, не очень хорошо представляя, каким образом воспользоваться полученной системой из нескольких дифференциальных уравнений и замыкающих соотношений, описывающих один или несколько элементов энергетической установки. К сожалению, рекомендации по «правильному» началу собственного пути в моделировании встречаются в литературе очень редко. Поэтому, автор считает полезными некоторые пояснения о реализации модели на элементарном примере.

Как уже указывалось выше существует ряд различных по сложности методов решения дифференциальных уравнений (см. гл. 2) сохранения, среди которых для «точечных» моделей своей простотой выделяется «одношаговый» метод Эйлера. На примере его применения понять способ решения системы уравнений и реализации модели достаточно легко.

Прежде всего следует помнить, что динамический процесс имеет аргументом (независимой переменной) время, что справедливо для большинства расчитываемых на модели функций, которые чаще всего являются ведущими технологическими параметрами такого процесса. Поэтому большинство получаемых на модели зависимостей являются фукциями времени. Любой из существующих способов решения систем дифференциальных уравнений позволяет найти значения конкретных функций в определенные моменты времени, а не отлеживать ее изменения непрерывно. Чем ближе друг к другу эти моменты времени (этот временной интервал называют шагом интегрирования), тем точнее найдено значение конкретной функции. Правда, чем мельче шаг интегрирования, чем больше расчетных шагов надо сделать, чтобы расчитать изменение функции на одном и том же интервале времени.

Расчет каждого нового значения функции возможен, если известны ее старые значения или, как говорят, «значения функции на предыдущих шагах». Для одиночного дифференциального уравнения:

,(5.1)

Здесь : · новое значение функции;

· предыдущее (известное) значение функции;

· приращение функции на данном временном шаге.

Таким образом, определение нового значения конкретной интегрируемой функции требует корректного вычисления приращения функции на одном временном шаге, являющимся приращением аргумента, т.е. времени.

Метод Эйлера требует знания лишь одного значения производной искомой функции на предыдущем шаге для определения величины приращения данной функции на следующем временном шаге:

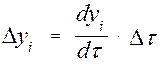, (5.2)

Метод легко проиллюстрировать на графике любой непрерывной дифференцируемой функции (см. Рис. 1) :

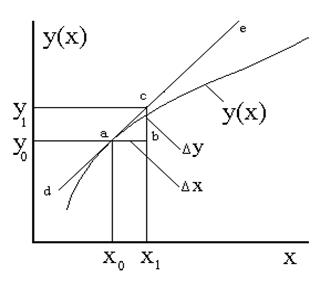
Рис. 1 Графическая интерпретация производной

На графике показана непрерывная на некотором интервале функция y(x), которая при начальном значении аргумента х₀ имеет значение y₀. К графику функции в данной точке проведена касательная (de), образующая с осью абсцисс (в нашем случае - шкалой времени) острый угол Ðcab. Тангенс этого угла есть не что иное, как производная функции y(x). Из графика следует, что искомое значение функции y₁ при значении аргумента x₁, т.е. при

шаге интегрирования Dх = x₁ - х₀ может быть приблизительно найдено, как y₁ = y₀ + Dy, где Dy - приращение функции y(x), есть катет «bc» треугольника «cab», который из геометрического построения может быть найден через другой катет «ab», или, что то же самое, через приращение аргумента (шаг интегрирования) Dх: Dy = Dх × tg(cab). Однако, поскольку tg(cab) есть по смыслу производная функции y(x), то это дает основание записать выражение для приращения функции на шаге, как:

,

что подтверждает справедливость выражений (5.1) и (5.2) для поиска приращения функции и самого ее нового значения. Понимание способа определения нового значения функции на очередном временном шаге через ее приращение является ключевым знанием при интегрировании систем дифференциальных уравнений.

Таким образом, алгоритм реализации моделей энергооборудования, т.е. решения систем дифференциальных уравнений с необходимыми замыкающими соотношениями можно представить в виде цикличной (регулярно повторяющейся) последовательности операций:

· найти значения всех производных из дифференциальных уравнений модели, уточнив где это необходимо значения коэффициентов и переменных величин, входящих в уравнения, с помощью замыкающих соотношений;

· с помощью полученных производных определить приращения для каждой интегрируемой функции на текущем временном шаге;

· сложить найденные приращения с имеемыми (предыдущими) значениями каждой интегрируемой функции, определить их новые значения;

· добавить к имеемому (старому) значению времени приращение аргумента, т.е. величину текущего шага интегрирования, определить тем самым новое значение текущего времени;

· вывести на печать (на график, в таблицу) значение текущего времени и соответствующие ему новые значения интегрируемых функций;

· проверить условие окончания решения системы уравнений: либо по достижении временем заданного значения, либо по достижении каким-либо параметром (функцией) некой предельной величины;

· при отсутствии указателя окончания счета вернуться к п. 1 и вновь продолжить расчет производных для интегрируемых функций.

Это наиболее общая схема применения теплогидравлической модели, разработанной на основе дифференциальных уравнений сохранения.