Главная | Обратная связь

Лекция 7. Метод Ньютона-Канторовича.

 

Рассмотрим уравнение

,

где - дифференцируемый по Фреше нелинейный оператор , где -открытое множество в 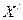. В дальнейшем удобно считать, что - шар.

Пусть - некоторое приближение к точному решению .

Основная идея метода основана на последовательной линеаризации уравнения .

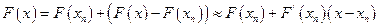
Линеаризованное уравнение

Предположим, что линейный оператор обратим. Тогда

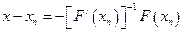
Итерационный метод, определенный формулой называется методом Ньютона-Канторовича. Ему посвящена многочисленная литература. Представляет интерес несколько аспектов:

1) Условия (эффективно проверяемые) осуществимости этого метода.

2) Оценки быстроты сходимости и априорные оценки погрешности.

3) Как находить такие начальные приближения 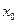, начиная с которых метод сходится

4) Вопросы устойчивости метода.

 

I) Локальное условие сходимости. Быстрота сходимости.

Рассмотрим оператор

Обозначим .

Исходное уравнение эквивалентно уравнению

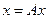
Уравнении можно решать методом последовательных приближений на основе результатов предыдущего параграфа. Ниже покажем, что , где -решение .

Теорема 1. Пусть существует ограниченный , непрерывен в . Тогда последовательные приближения сходятся к , если начальное приближение 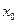достаточно близко к . Быстрота сходимости задается неравенством

,

где 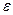- любое положительное число.

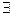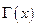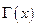Доказательство. По обобщенной теореме Банаха обратный в точка, близких к и непрерывна в .

Рассмотрим тождество

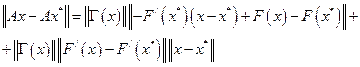
Отсюда , т.е. ; .

Результат теоремы вытекает из теоремы предыдущего параграфа.

Результат теоремы 1 можно существенно усилить, если известна какая-либо дополнительная информация о .

Теорема 2. Пусть в окрестности выполнено условие Липшица , где 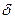можно сделать сколь угодно малым за счет выбора .

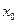Доказательство. Опираясь на лемму предыдущего параграфа достаточно доказать, что в некоторой окрестности .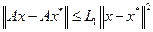

Рассмотрим тождество

, откуда

Пусть ;

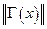- ограничена, откуда и следует вывод теоремы.

II. Нелокальное условие сходимости.

Пусть - дифференцируем в некотором шаре , где 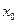- начальное приближение и 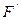удовлетворяет в этом шаре условию Липшица

Также предполагаем, что существует ограниченный обратный

Теорема. Пусть справедливы оценки

Пусть

Тогда последовательные приближения сходятся к решению уравнения , лежащему в шаре .

Доказательство (Канторовича).

Определим числовые последовательности

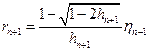, и покажем, что в условиях , последовательность сходится, причем

Для доказательства достаточно провести шаг индукции. Пусть и верны при . Докажем для .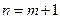

Очевидно

Легко проверить, что при

(Задача)

Из определения следует, что и тем более . Поэтому существует производная . В силу имеем

Из обобщенной теоремы Банаха следует (задача), что существует 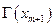и его можно представить в виде

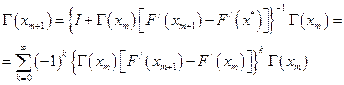
Отсюда получаем оценку

Перейдем к доказательству второго из неравенств для .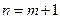

Из тождества (задача).

и из неравенства

(предыдущий пункт.)

следует

а в силу имеем

Докажем треть из неравенств .

Имеем

Для доказательства включения , достаточно заметить, что из вытекает неравенство

, т.к. правая часть тождественно равна (задача).

Из третьего неравенства вытекает, что , поэтому при . Следовательно последовательные приближения сходятся к некоторой точке . Переход к пределу в неравенстве завершает доказательство. Из доказательства видно, что в условиях данной теоремы справедлива оценка ,

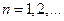
Задача. Пусть выполнены условия данной теоремы. Доказать, что

III. Простые нули.

Определение. Решение уравнения называется простым нулем оператора , если существует непрерывный обратный .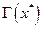

Теорема. Пусть выполнены условия предыдущей теоремы и . Тогда нуль оператора Ю к которому сходятся последовательные приближения , простой.

Доказательство. Докажем сначала, что из следует, что

Итак, пусть , тогда

Рассмотрим оператор

По теореме Банаха об обратном операторе - обратим, следовательно

также обратим.

Теорема доказана.

Замечание. Усилить результат теоремы нельзя, т.к. при для уравнения последовательные приближения сходятся для к кратному корню.

IV. Модифицированный метод Ньютона-Канторовича.

,

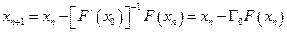Теорема. Пусть выполнены все условия теоремы, с той лишь разницей, что

 

 

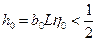
Тогда последовательные приближения сходятся к единственному решению уравнения в шаре

Доказательство. Покажем, что оператор , определенный равенством

 

 

удовлетворяет на шаре условиям принципа сжатых отображений, откуда следует заключение теоремы.

Рассмотрим тождество для любых 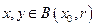, где .

 

Из этого тождества и из условия Липшица вытекает оценка

В шаре

,

следовательно является оператором сжатия на шаре . Чтобы завершить доказательство, осталось показать, что .

Пусть . Тогда, используя , получаем

.

Используя условие Липшица , получаем

.

Поэтому при

Теорема доказана.