 |
|
Лекция 11. Применения к интегральным уравнениям.
I. Уравнение Фредгольма
Предположим, что ядро 
непрерывно в квадрате 
Обозначим через 
интегральный оператор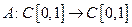 
по формуле
Лемма 1. Оператор является компактным и имеет норму
(Люстерник Соболев.)
Используя определение резольвенты, получаем, что если 
- неособенное значение параметра, то решение будет 
и по теореме 1. решение можно разложить в ряд
который сходится для всех 
, а по теореме 2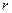 
есть расстояние от точки 
до характеристического множества . Сходимость ряда имеет место, в частности для
Лемма2. Операторы 
для 
являются интегральным операторами.
Доказательство. Обозначим 
, 
, т.е. 
; 
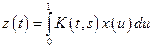
Отсюда
где 
По индукции аналогично доказывается, что 
означает, что
, 
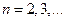
где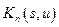 
определяется из рекуррентного соотношения
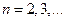
раскрыв которое, получим
Функции 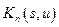называются повторными или итерированными ядрами.
Запишем теперь подробно ряд Неймана
Данный ряд сходится равномерно по 
Обозначим сумму ряда в квадратных скобках через 
- эта функция называется резольвентой интегрального уравнения .
Окончательно решение можно записать в виде
Теорема. Если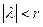 
, то уравнение можно решать методом последовательных приближений, исходя из любой непрерывной функции 
, т.е.
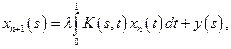
Т.к. оператор компактен, то справедлива альтернатива Фредгольма.
Теорема. Либо уравнение имеет единственное непрерывное решения для любой непрерывной функции 
, либо уравнение
имеет конечное число линейно независимых решений 
, …, 
.
Определение. Такие - называются характеристическими значениями уравнения . (они совпадают с характеристическими значениями оператора ).
Для наименьшего по модулю характеристического значения справедлива оценка
II. Уравнение Вольтерра.
Можно рассматривать как частный случай уравнение Фредгольма, у которого ядро при 
обращается в нуль.
Повторные ядра также обарщаются в 0 при 
.
Докажем, что радиус сходимости ряда Неймана равен 
, т.е. справедлива при 
.
Пусть 
.
Лемма. Для каждого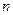 
справедлива оценка
Доказательство. 
- очевидно. Пусть верна для 
, докажем для 
Из оценки получаем
Отсюда 
.
Значим 
; 
, т.е. нет характеристических значений.