Главная | Обратная связь

ПОЛНОТА МЕТОДА РЕЗОЛЮЦИЙ ДЛЯ ЛОГИКИ ПРЕДИКАТОВ

Теорема. Множество дизъюнктов S невыполнимо тогда и только тогда, когда из S выводим пустой дизъюнкт.

Доказательство. Пусть множество дизъюнктов S невыполнимо и B={A₁,A₂,…,A_n,…} – эрбрановский базис для S. Рассмотрим полное семантическое дерево Т:

 

 

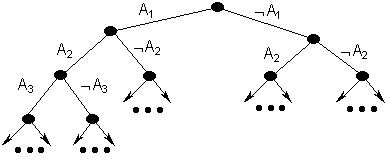
Через I(р) будем обозначать объединение всех литералов, принадлежащим дугам ветви р.

Через I(v) будем обозначать объединение всех литералов, принадлежащим дугам пути от корня до вершины v.

Определение. Семантическое дерево Т называется полным, если для любого элемента А из эрбрановского базиса B и для любой ветви р множество I(p) содержит либо А, либо А.

Определение. Вершина v семантического дерева называется опровергающей, если I(v) опровергает основной пример некоторого дизъюнкта S. Вершина v называется максимальной опровергающей, если вершина v′, предшествующая v, опровергающей не является.

Определение. Семантическое дерево называется замкнутым, если каждый его лист является максимальной опровергающей вершиной.

Докажем сначала, что справедлива следующая

Теорема 2 (Эрбран). Множество дизъюнктов S невыполнимо тогда и только тогда, когда любое полное семантическое дерево множества S имеет конечное замкнутое корневое поддерево.

Доказательство теоремы использует известное в математике утверждение, которое называется леммой Кенига.

Лемма. Если Т – бесконечное дерево, из каждого узла которого выходит конечное число дуг. Тогда дерево Т содержит бесконечный p путь, начинающийся от корня.

Доказательство леммы Кенига приводить не будем.

Необходимость. Пусть множество дизъюнктов S невыполнимо и Т – полное семантическое дерево для S. Рассмотрим произвольную ветвь p в дереве Т. По определению полного семантического дерева для каждой атомарной формулы А эрбрановского базиса B, либо А, либо А принадлежит I(p). Это означает, что I(p) есть H-интерпретация множества S. Поскольку S невыполнимо, то I(p) опровергает основной пример D′ некоторого дизъюнкта D из S. Дизъюнкт D′ конечен, поэтому ветвь p должна проходить через максимальную опровергающую вершину дерева Т. В каждой ветви отметим такую вершину. Пусть Т′ – корневое поддерево дерева Т, листьями которого являются отмеченные вершины. В силу леммы Кенига Т′ – конечное поддерево дерева Т. Дерево T′ по построению является замкнутым. Необходимость доказана.

Достаточность. Пусть полное семантическое дерево Т содержит конечное замкнутое корневое поддерево T′. По определению корневого поддерева следует, что каждая ветвь дерева Т содержит опровергающую вершину. Множество всех ветвей полного семантического дерева исчерпывает все H-интерпретации множества S. Следовательно, S ложно при всех H-интерпретациях. По первой теореме Эрбрана S невыполнимо.

Теорема Эрбрана доказана полностью.

 

Продолжим доказательство теоремы о полноте метода резолюций.

Согласно этой теореме Эрбрана Т содержит конечное замкнутое семантическое поддерево Т^/.

Если Т^/ состоит только из корня, то □ є S и поэтому □ выводим из S. Предположим, что Т^/ состоит не только из корня. Тогда Т^/ имеет вершину v, потомки v₁ и v₂ которой являются максимальными опровергающими для множества S вершинами. Пусть

I(v)={L₁, L₂,…, L_k},

I(v₁)={L₁, L_2,…,L_k, A_k+1},

I(v₂)={L₁, L₂,…, L_k, A_k+1}.

Существует дизъюнкт D₁ є S такой, что его основной пример D₁^/ опровергается в I(v₁), и существует дизъюнкт D₂ є S такой, что его основной пример D₂^/ опровергается в I(v₂). Так как дизъюнкты D₁^/ и D₂^/ не опровергаются в I(v), то D₁^/ содержит A_k+1, а D₂^/ – A_k+1. Применим к D₁^/ и D₂^/ правило резолюции, отрезая литералы A_k+1 и A_k+1, получим дизъюнкт D^/:

 

D^/=(D₁^{/ –} A_k+1) U (D₂^/ – A_k+1).

 

Отметим, что дизъюнкт D₁^/ – A_k+1 ложен в I(v), поскольку в противном случае, D₁^/ был бы истинен в I(v₁). Аналогично заключаем, что D₂^/ – A_k+1 ложен в той же интерпретации I(v).

Отсюда следует, что D^/ ложен при I(v).

По лемме о подъеме существует дизъюнкт D, который является резольвентой дизъюнктов D₁ и D₂. Ясно, что его основной пример D^/ опровергается в I(v). Рассмотрим множество дизъюнктов S U {D}. Замкнутое семантическое дерево T^// для этого множества дизъюнктов можно получить вычеркиванием некоторых вершин (и идущих в них дуг) дерева T^/. А именно, в дереве T^/ вычеркиваем все дуги и вершины, которые лежат ниже первой вершины, где дизъюнкт D^/ ложен. Полученное таким образом дерево T^// содержит меньше вершин, нежели дерево T^/, так как v₁,v₂ є T^//.

Применим описанный выше процесс к T^//, мы получим резольвенту дизъюнктов из S U {D}. Расширим множество S U {D} за счет этой резольвенты, придем к конечному замкнутому дереву с меньшим числом вершин, нежели T^//. В конце концов, получим замкнутое семантическое дерево, состоящее только из корня. Это возможно, лишь в случае, когда множество S, расширенное резольвентами, содержит пустой дизъюнкт, Следовательно, □ выводим из S. Необходимость условия теоремы доказана.

Докажем достаточность. Пусть пустой дизъюнкт выводим из S, и D₁,D₂,…,D_n=□ – вывод из S. Предположим, что S выполнимо в некоторой интерпретации. Тогда, поскольку правило резолюции сохраняет истинность, то все дизъюнкты вывода, в том числе и пустой, являются истинными в этой интерпретации. Полученное противоречие доказывает, что S невыполнимо.

Теорема доказана.