 |
|
Штрихи и многоточия
НАБОР ФОРМУЛ
Основные принципы
В документе, подготовленном с помощью TeX'а, различают математические формулы внутри текста и " выключные" (выделенные в отдельную строку). Формулы внутри текста окружаются знаками $ (с обеих сторон). Выключные формулы окружаются парами знаков доллара $$ с обеих сторон. Формулами считаются как целые формулы, так и отдельные цифры или буквы, в том числе греческие, а также верхние и нижние индексы и спецзнаки. Пробелы внутри исходного текста, задающего формулу, игнорируются (но по-прежнему надо ставить пробелы, обозначающие конец команды): TeX расставляет пробелы в математических формулах автоматически (например, знак равенства окружается небольшими пробелами). Пустые строки внутри текста, задающего формулу, не разрешаются. Если нужен пробел до или после внутритекстовой формулы, надо оставить его вне долларов. То же самое относится и к знакам препинания, следующим за внутритекстовой формулой: их также надо ставить после закрывающего формулу знака доллара. (В выключных формулах приходится указывать знаки препинания внутри долларов, иначе эти знаки попадут на следующую строку.) Каждая буква в формуле рассматривается как имя переменной и набирается шрифтом " математический курсив" (в отличие от обычного курсива, в нем увеличены расстояния между соседними буквами).
Часть файла, составляющая математическую формулу, образует группу : изменения параметров, произведенные внутри формулы, забываются по ее окончании.
Степени и индексы
Степени и индексы набираются с помощью знаков "^" и "_" соответственно.
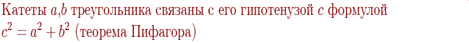 .
.
| Катеты $a$,$b$ треугольника связаны с его гипотенузой $c$ формулой $c^2=a^2+b^2$ (теорема Пифагора). |
Если индекс или показатель степени - выражение, состоящее более чем из одного символа, то его надо взять в фигурные скобки:
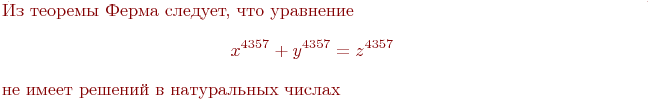 .
.
| Из теоремы Ферма следует, что уравнение $$ x^{4357}+y^{4357}=z^{4357} $$ не имеет решений в натуральных числах. |
Если у одной буквы есть как верхние, так и нижние индексы, то можно указать их в произвольном порядке:
 .
.
| Обозначение $R^i_{jkl}$ для тензора кривизны было введено еще Эйнштейном. |
Если же требуется, чтобы верхние и нижние индексы располагались не друг под другом, а на разных расстояниях от выражения, к которому они относятся, то нужно немного обмануть TeX, оформив часть индексов как индексы к "пустой формуле" (паре из открывающей и закрывающей скобок):
 .
.
| Можно также написать $R_j{}^i{}_{kl}$, хотя не всем это нравится. |
Если вы хотите написать формулу, читающуюся как "два в степени, равной икс в кубе", то запись "2^x^3" вызовет сообщение об ошибке; правильно будет "2^{x^3}" (на печати это будет выглядеть как 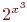 ).
).
Дроби
Дроби, обозначаемые косой чертой (так рекомендуется обозначать дроби во внутритекстовых формулах), набираются непосредственно:
 .
.
| Неравенство $x+1/x\ge 2$ выполнено для всех $x>0$. |
В этом примере мы еще использовали знаки "строгих" неравенств (в TeX'овских формулах они набираются непосредственно, как знаки ">" и "<") и нестрогих неравенств (знак "больше или равно" генерируется командой \ge, "меньше или равно" — командой \le). Если вы употребите символы "<" и ">" в обычном тексте, вне формул, то вместо знаков "меньше" и "больше" увидите небольшой сюрприз.
Наряду со знаками для нестрогих неравенств, TeX предоставляет большое количество специальных символов для математических формул (греческие буквы также рассматриваются как специальные символы). Все эти символы набираются с помощью специальных команд (не требующих параметров). Списки этих команд вы найдете в таблицах в начале следующей лекции.
Если вы используете в формуле десятичные дроби, в которых дробная часть отделена от целой с помощью запятой, то эту запятую следует взять в фигурные скобки (в противном случае после нее будет оставлен небольшой дополнительный пробел, что нежелательно):

| \pi\approx 3{,}14 |
Здесь команда \pi порождает греческую букву 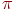 , а команда \approx дает знак
, а команда \approx дает знак  (" приближенно равно"). Десятичную точку в дробях заключать в скобки не нужно.
(" приближенно равно"). Десятичную точку в дробях заключать в скобки не нужно.
Дроби, в которых числитель расположен над знаменателем, набираются с помощью команды \frac.Эта команда имеет два обязательных аргумента: первый - числитель, второй - знаменатель.
Пример:
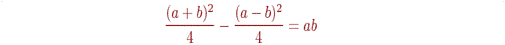
| $$ \frac{(a+b)^2}{4}- \frac{(a-b)^2}{4}=ab $$ |
Если числитель и\или знаменатель дроби записываются одной буквой (в том числе греческой) или цифрой, то можно их и не брать в фигурные скобки:

| $$ \frac12+\frac x 2= \frac{1+x}2 $$ |
Скобки
Круглые и квадратные скобки набираются как обычно, для фигурных скобок используются команды \{ и \},для других также есть специальные команды (см. следующую лекцию).
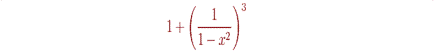
| $$1+\left(\frac{1}{1-x^{2}}\right)^3$$ |
Команда \left перед открывающей скобкой в совокупности с командой \right перед соответствующей ей закрывающей скобкой позволяет автоматически выбрать нужный размер скобки:
Подробнее о скобках, размер которых выбирается автоматически, рассказано в следующей лекции .
Корни
Квадратный корень набирается с помощью команды \sqrt, обязательным аргументом которой является подкоренное выражение; корень произвольной степени набирается с помощью той же команды \sqrt с необязательным аргументом — показателем корня (необязательный аргумент у этой команды ставится перед обязательным). Пример:
 .
.
| По общепринятому соглашению, $\sqrt[3]{x^3}=x$, но $\sqrt{x^2}=|x|$. |
Обратите внимание, что вертикальные черточки, обозначающие знак модуля, набираются непосредственно.
Штрихи и многоточия
Штрихи в математических формулах обозначаются знаком "'" (и не оформляются как верхние индексы):
 .
.
| Согласно формуле Лейбница,$$(fg)''=f''g+2f'g'+fg''.$$Это похоже на формулуквадрата суммы. |
Если надо записать формулу, читающуюся как "  штрих в квадрате", возьмите x' в фигурные скобки, вот так: ${x'}^2$. Обратите еще внимание на то, что точку мы поставили в конце выключенной формулы (если бы мы поставили ее после знаков $$, то с нее начался бы абзац, следующий после формулы).
штрих в квадрате", возьмите x' в фигурные скобки, вот так: ${x'}^2$. Обратите еще внимание на то, что точку мы поставили в конце выключенной формулы (если бы мы поставили ее после знаков $$, то с нее начался бы абзац, следующий после формулы).
В математических формулах встречаются многоточия; TeX различает многоточие, расположенное внизу строки (обозначается\ldots ), и расположенное по центру строки (оно обозначается \cdots ). Первое из них используется при перечислениях, второе — когда нужно заменить пропущенные слагаемые или сомножители (такова американская традиция; в России обычно многоточие ставят внизу строки и в этом случае):
 .
.
| В детстве К~.-Ф.~Гаусс придумал,как быстро найти сумму$$1+2+\cdots+100=5050;$$это случилось, когда школьныйучитель задал классу найтисумму чисел $1,2,\ldots,100$. |
Знак "~" после инициалов великого Гаусса мы поставили, чтобы фамилия не могла перенестись на другую строку отдельно от инициалов. В LaTeX'е можно использовать команду \ldots и в обычном тексте, вне математических формул, для знака многоточия.
Имена функций
Функции наподобие 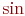 ,
, 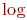 и т.п., имена которых принято печатать прямым шрифтом, набираются с помощью специальных команд (обычно одноименных с обозначениями соответствующих функций).
и т.п., имена которых принято печатать прямым шрифтом, набираются с помощью специальных команд (обычно одноименных с обозначениями соответствующих функций).
 .
.
| Как знают некоторые школьники,$\log_{1/16}2=-1/4$,а $\sin(\pi/6)=1/2$. |
Заметьте, что основание логарифма задается как нижний индекс.