 |
|
Свойства умножения матриц.
Для любых матриц  K
K 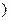 ,
,  K
K 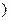 ,
,  K
K 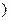 и любого числа
и любого числа
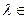 Kсправедливы равенства:
Kсправедливы равенства:
1.  (ассоциативность умножения);
(ассоциативность умножения);
2.  (дистрибутивность по первому сомножителю);
(дистрибутивность по первому сомножителю);
3.  (дистрибутивность по второму сомножителю);
(дистрибутивность по второму сомножителю);
4.  ;
;
5.  ;
;
6.  .
.
Доказательство.
1. Из определения 1 следует, что произведения 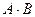 ,
,  ,
,  и
и  имеют смысл и две последние матрицы имеют строение
имеют смысл и две последние матрицы имеют строение 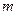 на
на  . Следовательно, нужно доказать, что в равенстве 1 в обеих частях на одинаковых местах стоят равные элементы.
. Следовательно, нужно доказать, что в равенстве 1 в обеих частях на одинаковых местах стоят равные элементы.
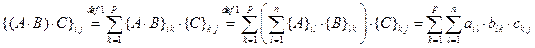 , где
, где 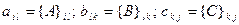 . Теперь рассмотрим элемент матрицы
. Теперь рассмотрим элемент матрицы  , стоящий в
, стоящий в  - ой строке и
- ой строке и  - ом столбце:
- ом столбце: 
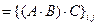 для всех
для всех  . Следовательно,
. Следовательно,  .
.
2. Из определения 1 следует, что матрицы  ,
, 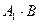 ,
, 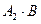 в равенстве 2 определены и имеют одинаковое строение
в равенстве 2 определены и имеют одинаковое строение 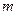 на
на 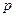 . Следовательно, матрицы в обеих частях равенства 2 имеют одинаковое строение и нужно доказать, что в обеих частях на одинаковых местах стоят равные элементы.
. Следовательно, матрицы в обеих частях равенства 2 имеют одинаковое строение и нужно доказать, что в обеих частях на одинаковых местах стоят равные элементы.
Рассмотрим элемент 

 для всех
для всех 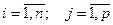 . Здесь мы воспользовались ещё определением сложения матриц, коммутативностью, ассоциативностью и дистрибутивностью для чисел.
. Здесь мы воспользовались ещё определением сложения матриц, коммутативностью, ассоциативностью и дистрибутивностью для чисел.
Следовательно, по определению 8 справедливо равенство  .
.
Свойство 3 (дистрибутивность по второму сомножителю), которое доказывается аналогично свойству 2, предлагается доказать самостоятельно.
4. Из определения 1 и определения умножения матрицы на число следует, что матрицы  ,
,  ,
,  определены и имеют одинаковое строение
определены и имеют одинаковое строение 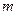 на
на 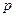 . Следовательно, нужно доказать, что в обеих частях равенства 4 на одинаковых местах стоят равные элементы.
. Следовательно, нужно доказать, что в обеих частях равенства 4 на одинаковых местах стоят равные элементы.

 для всех
для всех 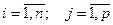 .
.
Следовательно,  . Здесь мы воспользовались ещё определением умножения матрицы на число, ассоциативностью и дистрибутивностью для чисел.
. Здесь мы воспользовались ещё определением умножения матрицы на число, ассоциативностью и дистрибутивностью для чисел.
Равенство  , которое доказывается аналогично предыдущему, предлагается доказать самостоятельно.
, которое доказывается аналогично предыдущему, предлагается доказать самостоятельно.
5. Из определения 1 следует, что матрицы  и
и  определены и имеют одинаковое строение
определены и имеют одинаковое строение 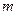 на
на  . Следовательно, все матрицы в равенствах 5 имеют одинаковое строение и нужно доказать, что на одинаковых местах стоят равные элементы.
. Следовательно, все матрицы в равенствах 5 имеют одинаковое строение и нужно доказать, что на одинаковых местах стоят равные элементы.
 для всех
для всех  .
.
Следовательно,  . Аналогично доказывается равенство
. Аналогично доказывается равенство  .
.
6. Из определения 1 следует, что обе матрицы  и
и  имеют одинаковое строение
имеют одинаковое строение  на
на  , причём все элементы обеих матриц равны нулю. Следовательно,
, причём все элементы обеих матриц равны нулю. Следовательно,  . Аналогично доказывается равенство
. Аналогично доказывается равенство  .
.
Замечание 1. Пусть 
 K
K 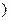 .Тогда в силу ассоциативности умножения матриц справедливо равенство
.Тогда в силу ассоциативности умножения матриц справедливо равенство  . Таким образом, способ расстановки скобок в этом произведении безразличен, так же, как и способ расстановки скобок в произведении
. Таким образом, способ расстановки скобок в этом произведении безразличен, так же, как и способ расстановки скобок в произведении  . Отсюда получаем, корректность следующего определения.
. Отсюда получаем, корректность следующего определения.
Определение 2. Пусть 
 K
K 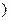 ,
,  N
N  .
.
 .
.
Замечание 2.Равенство 1 верно и в случае, если матрицы  и
и 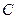 имеют указанное выше строение, причём элементами одной из них являются векторы, а элементами двух других - числа.
имеют указанное выше строение, причём элементами одной из них являются векторы, а элементами двух других - числа.
Аналогичные замечания справедливы и для остальных свойств.
Например,  , где
, где 
 R
R 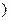 ,а
,а  - векторы.
- векторы.