 |
|
Метод переменных состояния
Идея метода состоит в выделении таких искомых величин, которые определяют энергетическое состояние электрической цепи, т.к. переходный процесс и есть процесс перехода от одного установившегося энергетического состояния к другому. А так как энергетическое состояние в линейных электрических цепях полностью определяется токами индуктивных катушек и напряжениями конденсаторов, то, очевидно, что в качестве искомых величин, определяющих состояние цепи, выбирают именно их.
Т.о., идея метода состоит в выделении в качестве искомых величин токов индуктивных катушек и напряжений конденсаторов.
Токи индуктивных катушек и напряжения конденсаторов называют переменными состояния.
Токи и напряжения резистивных элементов схемы, называемые выходными величинами, всегда могут быть выражены через переменные состояния при помощи законов Кирхгофа.
Очевидно, что в системе диф. уравнений для электрической цепи любой конфигурации, составленной по законам Кирхгофа, входят только первые производные переменных состояния.
Это позволяет для послекоммутационной схемы вместо одного неоднородного дифференциального уравнения n-го порядка получить n дифференциальных уравнений первого порядка относительно выбранных переменных состояния (уравнения состояния). Метод наиболее универсален для анализа электрических цепей и может быть легко приспособлен для расчета на ЭВМ.
Поэтому, разрешив исходную систему дифференциальных уравнений, составленную по законам Кирхгофа, относительно переменных состояния, получают систему дифференциальных уравнений 1-го порядка относительно переменных состояния для численного решения которой можно использовать стандартное математическое обеспечение ЭЦВМ (или аналоговых вычислительных машин.)
Под численными методами решения дифференциальных уравнений понимают методы, дающие приближенное решение в виде дискретного набора значений функции при некоторых значениях аргумента (Метод Рунге-Кутта, метод Пикара, метод Милна, экстраполяционный метод Адамса, метод с использованием ряда Тейлора).
Из теории дифференциальных уравнений известно, что всякое уравнение или система уравнений разрешенная относительно старших производных всех искомых функций  может быть приведена путем введения новых неизвестных функций к нормальной форме Коши:
может быть приведена путем введения новых неизвестных функций к нормальной форме Коши:


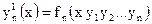
Задача нахождения решения уравнений при заданных начальных данных называется задачей Коши.
Алгоритм расчета
1. Составляем дифференциальные уравнения для производных от переменных состояния (уравнения состояния).
Для этого составляем уравнения по законам Кирхгофа для послекоммутационной схемы и решаем их относительно производных переменных состояния в зависимости от самих переменных состояния 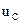 и
и 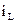 , источников э.д.с. и токов.
, источников э.д.с. и токов.
Получаем систему дифференциальных уравнений первого порядка относительно переменных состояний.
2. Уравнения состояния записываем в матричной форме и решаем аналитически или численными методами с использованием стандартного математического обеспечения ЭЦВМ (Метод Рунге-Кутта, Эйлера, трапеции, Пикара, Милна, экстраполяционный метод Адамса, метод с использованием ряда Тейлора).

где  – квадратная матрица порядка n;
– квадратная матрица порядка n;
 – матрица размера
– матрица размера  , где q –общее число источников э.д.с. и тока;
, где q –общее число источников э.д.с. и тока;
X – столбцовые матрицы размера  переменных состояния и их производных:
переменных состояния и их производных:  ;
;
V – столбцовая матрица размера  напряжений источников э.д.с. и токов источников тока.
напряжений источников э.д.с. и токов источников тока.
Элементы  и
и  определяются только параметрами схемы и ее топологией.
определяются только параметрами схемы и ее топологией.
3. Токи и напряжения резистивных элементов схемы, называемые выходными параметрами, всегда могут быть выражены и рассчитаны через переменные состояния при помощи законов Кирхгофа.
В результате получим систему алгебраических уравнений, устанавливающую связь между искомыми выходными параметрами, переменными состояния и источниками энергии (уравнения выходных параметров).
4. Записываем уравнения для выходных параметров в матричной форме и решаем их аналитически или с помощью ЭЦВМ.
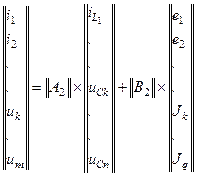 или
или 
где Y – столбцовая матрица размера 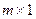 выходных параметров;
выходных параметров;
m – число выходных параметров;
 – матрицы размера
– матрицы размера  и
и  , элементы которых определяются параметрами и топологией схемы.
, элементы которых определяются параметрами и топологией схемы.
Пример 1:


Учтем, что 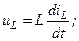
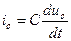 . Тогда
. Тогда  .
.
Пример 2:

 .
.
Учтем, что 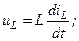
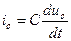 . Тогда
. Тогда
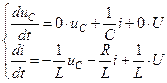 .
.
Пример 3:

 .
.
Учтем, что 
 . Тогда
. Тогда
 .
.