 |
|
Теоретические упражнения.
VI. РЯДЫ
Теоретические вопросы
1. Сходимость и сумма ряда. Необходимое условие сходимости ряда.
2. Теоремы сравнения.
3. Признаки Даламбера и Коши.
4. Интегральный признак сходимости ряда.
5. Теорема Лейбница. Оценка остатка знакочередующегося ряда.
6. Теорема о сходимости абсолютно сходящегося ряда. Свойства абсолютно сходящегося ряда.
7. Понятие равномерной сходимости.
8. Теорема о непрерывности суммы функционального ряда.
9. Теоремы о почленном интегрировании и почленном дифференцировании функционального ряда.
10. Теорема Абеля. Интервал и радиус сходимости степенного ряда.
11. Теорема о равномерной сходимости степенного ряда. Непрерывность суммы ряда.
12. Почленное интегрирование и дифференцирование степенных рядов.
13. Разложение функции в степенной ряд. Ряд Тейлора.
14. Разложение по степеням 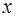 бинома
бинома  .
.
15. Условие разложимости функции в ряд Тейлора.
16. Разложение по степеням 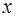 функций
функций 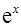 ,
, 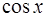 ,
,  ,
,  .
.
Теоретические упражнения.
1. Ряды 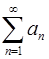 и
и 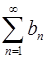 сходятся. Доказать, что ряд
сходятся. Доказать, что ряд 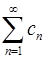 сходится, если
сходится, если 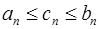 .
.
У к а з а н и е. Рассмотреть неравенства 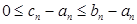 .
.
2. Ряд 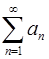
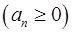 сходится. Доказать, что ряд
сходится. Доказать, что ряд 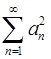 тоже сходится. Показать, что обратное утверждение неверно.
тоже сходится. Показать, что обратное утверждение неверно.
3. Ряды 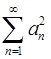 и
и  сходятся. Доказать, что ряд
сходятся. Доказать, что ряд  тоже сходится.
тоже сходится.
У к а з а н и е. Доказать и использовать неравенство 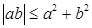 .
.
4. Ряды 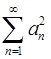 и
и  сходятся. Доказать, что ряд
сходятся. Доказать, что ряд  тоже сходится.
тоже сходится.
5. Пусть ряд 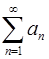 сходиться и
сходиться и 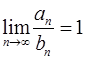 . Можно ли утверждать, что сходиться ряд
. Можно ли утверждать, что сходиться ряд 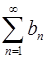 ?
?
Рассмотреть пример 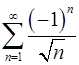 и
и 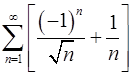 .
.
6. Пусть ряд 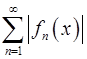 сходиться равномерно на отрезке
сходиться равномерно на отрезке 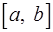 . Доказать, что ряд
. Доказать, что ряд 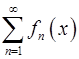 так же сходиться равномерно на этом отрезке.
так же сходиться равномерно на этом отрезке.
7. Может ли функциональный ряд на отрезке:
а) сходиться равномерно и не сходиться абсолютно,
б) сходиться абсолютно и не сходиться равномерно?
Рассмотреть примеры:
a)  , отрезок
, отрезок 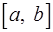 произвольный;
произвольный;
б)  , отрезок
, отрезок 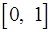 .
.
8. Показать, что функция 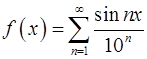 всюду непрерывна.
всюду непрерывна.
9. Доказать, что ряд 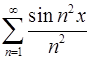 сходится равномерно в интервале
сходится равномерно в интервале  . Можно ли его дифференцировать в этом интервале?
. Можно ли его дифференцировать в этом интервале?
10. Доказать, что если ряд 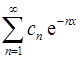 сходиться в точке
сходиться в точке 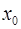 , то он сходиться абсолютно
, то он сходиться абсолютно  .
.
Расчетные задания.
 Задача 1.Найти сумму ряда.
Задача 1.Найти сумму ряда.
1.1.  . 1.2.
. 1.2. 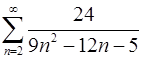 .
.
1.3. 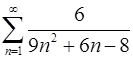 . 1.4.
. 1.4. 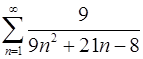 .
.
1.5. 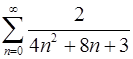 . 1.6.
. 1.6. 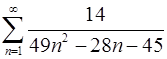 .
.
1.7. 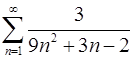 . 1.8.
. 1.8.  .
.
1.9. 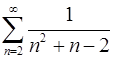 . 1.10.
. 1.10. 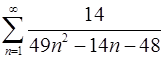 .
.
1.11. 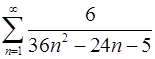 . 1.12
. 1.12  .
.
1.13  . 1.14
. 1.14 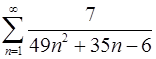 .
.
1.15. 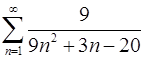 . 1.16
. 1.16 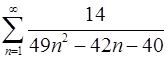 .
.
1.17. 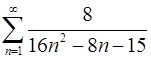 . 1.18.
. 1.18.  .
.
1.19. 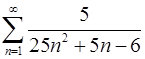 . 1.20.
. 1.20. 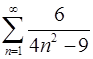 .
.
1.21. 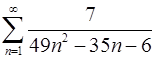 . 1.22.
. 1.22. 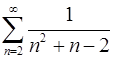 .
.
1.23.  . 1.24.
. 1.24.  .
.
1.25  . 1.26.
. 1.26. 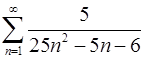 .
.
1.27. 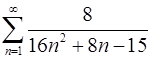 . 1.28.
. 1.28.  .
.
1.29. 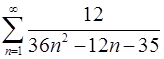 . 1.30.
. 1.30. 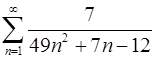 .
.
1.31. 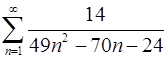 .
.
Задача 2.Найти сумму ряда.
2.1.  2.2
2.2 
2.3.  2.4.
2.4. 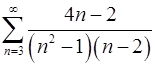 .
.
2.5. 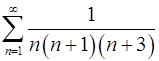 . 2.6.
. 2.6.  .
.
2.7. 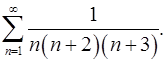 2.8.
2.8. 
2.9. 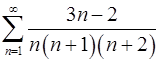 . 2.10.
. 2.10. 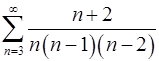 .
.
2.11. 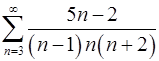 . 2.12.
. 2.12. 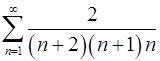 .
.
2.13. 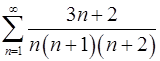 . 2.14.
. 2.14.  .
.
2.15. 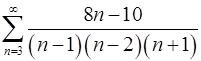 . 2.16.
. 2.16. 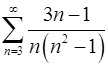 .
.
2.17.  . 2.18.
. 2.18. 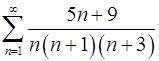 .
.
2.19. 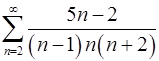 . 2.20.
. 2.20. 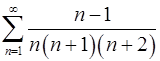 .
.
2.21.  . 2.22.
. 2.22.  .
.
2.23. 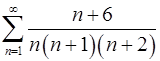 . 2.24.
. 2.24.  .
.
2.25. 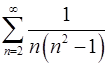 . 2.26.
. 2.26. 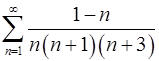 .
.
2.27. 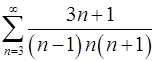 . 2.28.
. 2.28. 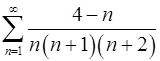 .
.
2.29. 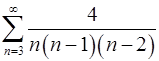 . 2.30.
. 2.30. 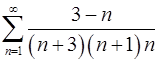 .
.
2.31. 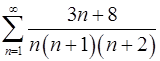 .
.
Задача 1.Исследовать на сходимость ряд.
3.1. 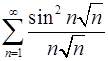 . 3.2.
. 3.2.  .
.
3.3. 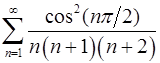 . 3.4.
. 3.4. 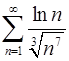 .
.
3.5.  . 3.6.
. 3.6.  .
.
3.7. 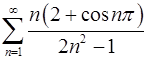 . 3.8.
. 3.8. 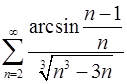 .
.
3.9. 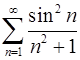 . 3.10.
. 3.10. 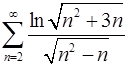 .
.
3.11. 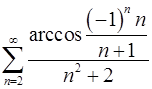 . 3.12.
. 3.12.  .
.
3.13. 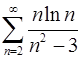 . 3.14.
. 3.14.  .
.
3.15. 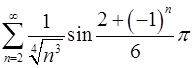 . 3.16.
. 3.16. 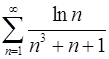 .
.
3.17. 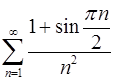 . 3.18.
. 3.18. 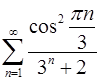 .
.
3.19. 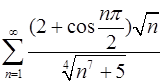 . 3.20.
. 3.20. 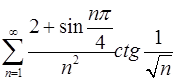 .
.
3.21. 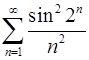 . 3.22.
. 3.22. 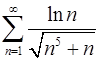 .
.
3.23.  . 3.24.
. 3.24. 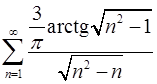 .
.
3.25.  . 3.26.
. 3.26. 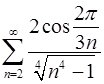 .
.
3.27. 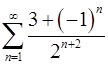 . 3.28.
. 3.28. 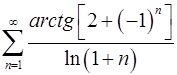 .
.
3.29. 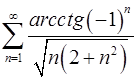 . 3.30.
. 3.30.  .
.
3.31.  .
.
Задача 4.Исследовать на сходимость ряд.
4.1.  . 4.2.
. 4.2. 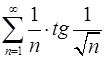 .
.
4.3. 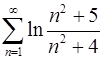 . 4.4.
. 4.4. 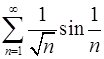 .
.
4.5. 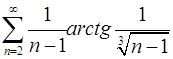 . 4.6.
. 4.6.  .
.
4.7.  . 4.8.
. 4.8. 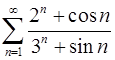 .
.
4.9.  . 4.10.
. 4.10. 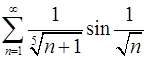 .
.
4.11. 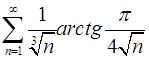 . 4.12.
. 4.12. 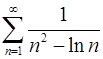 .
.
4.13.  . 4.14
. 4.14  .
.
4.15. 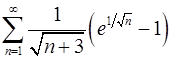 . 4.16.
. 4.16.  .
.
4.17. 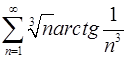 . 4.18.
. 4.18. 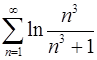 .
.
4.19. 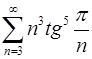 . 4.20.
. 4.20. 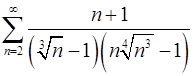 .
.
4.21.  . 4.22.
. 4.22. 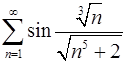 .
.
4.23. 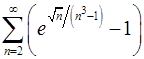 . 4.24.
. 4.24. 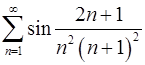 .
.
4.25. 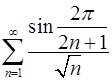 . 4.26.
. 4.26. 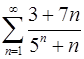 .
.
4.27.  . 4.28.
. 4.28. 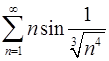 .
.
4.29. 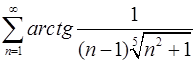 . 4.30.
. 4.30. 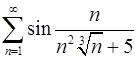 .
.
4.31.  .
.
Задача 5.Исследовать на сходимость ряд.
5.1.  . 5.2.
. 5.2.  .
.
5.3.  . 5.4.
. 5.4. 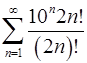 .
.
5.5. 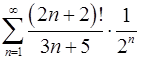 . 5.6.
. 5.6. 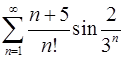 .
.
5.7. 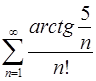 . 5.8.
. 5.8.  .
.
5.9.  . 5.10.
. 5.10. 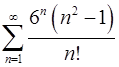 .
.
5.11. 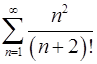 . 5.12.
. 5.12. 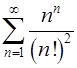 .
.
5.13. 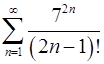 . 5.14.
. 5.14. 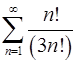 .
.
5.15.  . 5.16.
. 5.16. 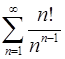 . ?
. ?
5.17.  . 5.18.
. 5.18. 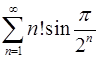 .
.
5.19.  . 5.20.
. 5.20. 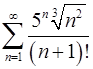 .
.
5.21. 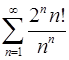 . 5.22.
. 5.22. 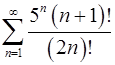 .
.
5.23. 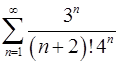 . 5.24.
. 5.24. 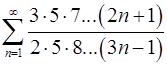 .
.
5.25. 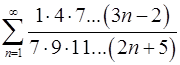 . 5.26.
. 5.26. 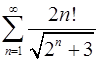 .
.
5.27.  . 5.28.
. 5.28. 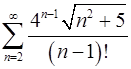 .
.
5.29. 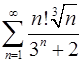 . 5.30.
. 5.30. 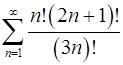 .
.
5.31. 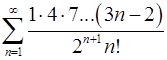 .
.
Задача 6.Исследовать на сходимость ряд.
6.1.  . 6.2.
. 6.2. 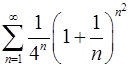 .
.
6.3.  . 6.4.
. 6.4.  .
.
6.5.  . 6.6.
. 6.6.  .
.
6.7. 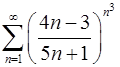 . 6.8.
. 6.8.  .
.
6.9. 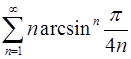 . 6.10.
. 6.10.  .
.
6.11. 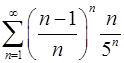 . 6.12.
. 6.12. 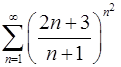 .
.
6.13.  . 6.14.
. 6.14. 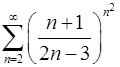 .
.
6.15. 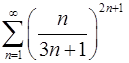 . 6.16.
. 6.16. 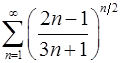 .
.
6.17. 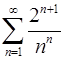 . 6.18.
. 6.18.  .
.
6.19. 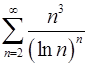 . 6.20.
. 6.20.  .
.
6.21. 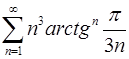 . 6.22.
. 6.22. 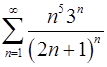 .
.
6.23.  . 6.24.
. 6.24.  .
.
6.25. 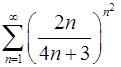 . 6.26.
. 6.26.  .
.
6.27. 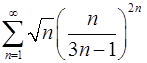 . 6.28.
. 6.28. 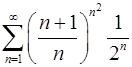 .
.
6.29. 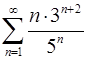 . 6.30.
. 6.30. 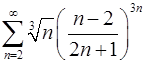 .
.
6.31. 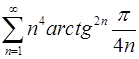 .
.
Задача 7.Исследовать на сходимость ряд.
7.1. 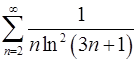 . 7.2.
. 7.2.  .
.
7.3.  . 7.4.
. 7.4. 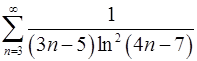 .
.
7.5. 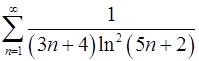 . 7.6.
. 7.6. 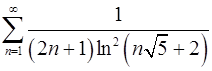 .
.
7.7. 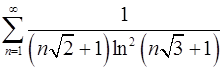 . 7.8.
. 7.8. 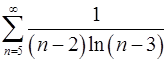 .
.
7.9. 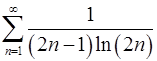 . 7.10.
. 7.10. 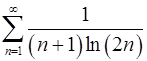 .
.
7.11. 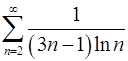 . 7.12.
. 7.12.  .
.
7.13.  . 7.14.
. 7.14.  .
.
7.15. 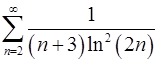 . 7.16.
. 7.16. 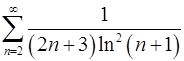 .
.
7.17. 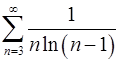 . 7.18.
. 7.18.  .
.
7.19. 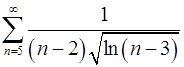 . 7.20.
. 7.20. 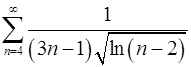 .
.
7.21.  . 7.22.
. 7.22.  .
.
7.23.  . 7.24.
. 7.24. 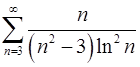 .
.
7.25. 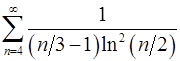 . 7.26.
. 7.26. 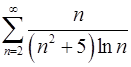 .
.
7.27. 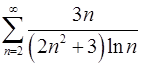 . 7.28.
. 7.28. 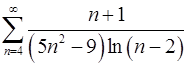 .
.
7.29. 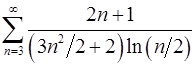 . 7.30.
. 7.30. 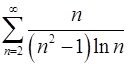 .
.
7.31. 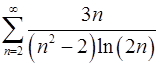 .
.
Задача 8.Исследовать на сходимость ряд.
8.1. 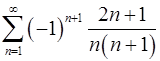 . 8.2.
. 8.2. 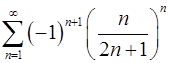 .
.
8.3. 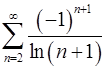 . 8.4.
. 8.4. 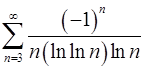 .
.
8.5. 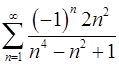 . 8.6.
. 8.6. 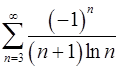 .
.
8.7.  . 8.8.
. 8.8. 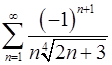 .
.
8.9. 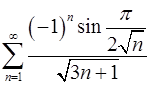 . 8.10.
. 8.10. 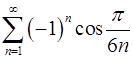 .
.
8.11.  . 8.12.
. 8.12. 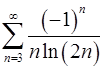 .
.
8.13. 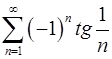 . 8.14.
. 8.14.  .
.
8.15. 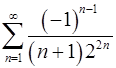 . 8.16.
. 8.16.  .
.
8.17. 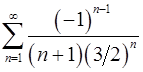 . 8.18.
. 8.18. 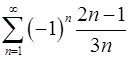 .
.
8.19.  . 8.20.
. 8.20.  .
.
8.21.  . 8.22.
. 8.22. 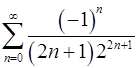 .
.
8.23. 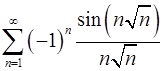 . 8.24.
. 8.24. 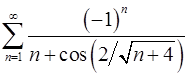 .
.
8.25. 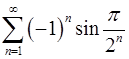 . 8.26.
. 8.26. 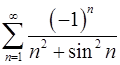 .
.
8.27. 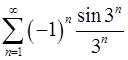 . 8.28.
. 8.28. 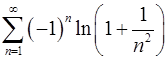 .
.
8.29.  . 8.30.
. 8.30. 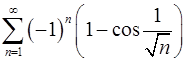 .
.
8.31. 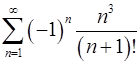 .
.
Задача 9.Вычислить сумму ряда с точностью 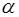 .
.
9.1. 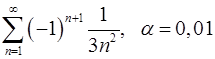 . 9.2.
. 9.2. 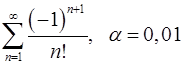 .
.
9.3. 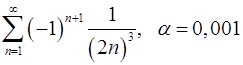 . 9.4.
. 9.4. 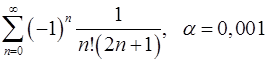 .
.
9.5. 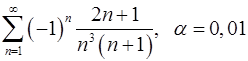 . 9.6.
. 9.6. 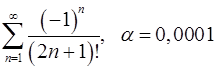 .
.
9.7. 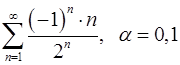 . 9.8.
. 9.8. 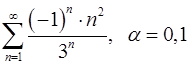 .
.
9.9. 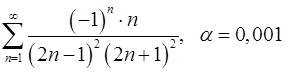 . 9.10.
. 9.10. 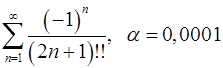 .
.
9.11.  . 9.12.
. 9.12.  .
.
9.13. 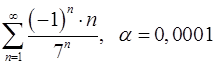 . 9.14.
. 9.14.  .
.
9.15. 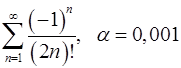 . 9.16.
. 9.16. 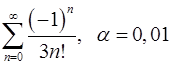 .
.
9.17. 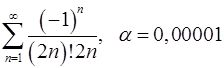 . 9.18.
. 9.18. 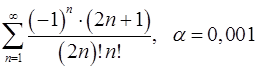 .
.
9.19. 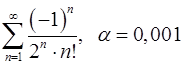 . 9.20.
. 9.20.  .
.
9.21. 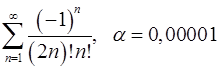 . 9.22.
. 9.22.  .
.
9.23.  . 9.24.
. 9.24. 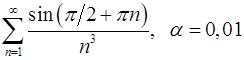 .
.
9.25.  . 9.26.
. 9.26. 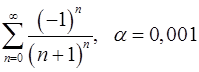 .
.
9.27. 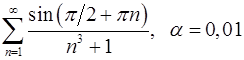 . 9.28.
. 9.28. 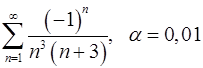 .
.
9.29. 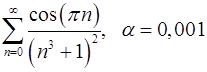 . 9.30.
. 9.30.  .
.
9.31.  .
.
Задача 10.Доказать справедливость равенства. (Ответом служит число 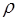 , получаемое при применении признака Даламбера или признака Коши.)
, получаемое при применении признака Даламбера или признака Коши.)
10.1. 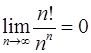 . 10.2.
. 10.2.  .
.
10.3. 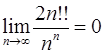 . 10.4.
. 10.4. 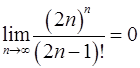 .
.
10.5. 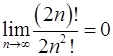 . 10.6.
. 10.6. 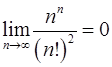 .
.
10.7. 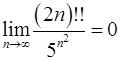 . 10.8.
. 10.8.  .
.
10.9. 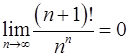 . 10.10.
. 10.10. 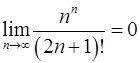 .
.
10.11.  . 10.12.
. 10.12. 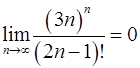 .
.
10.13. 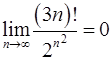 . 10.14.
. 10.14. 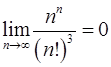 .
.
10.15. 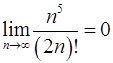 . 10.16.
. 10.16.  .
.
10.17. 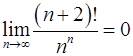 . 10.18.
. 10.18. 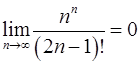 .
.
10.19. 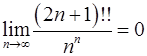 . 10.20.
. 10.20.  .
.
10.21.  . 10.22.
. 10.22.  .
.
10.23. 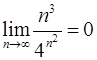 . 10.24.
. 10.24. 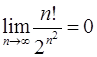 .
.
10.25. 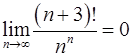 . 10.26.
. 10.26. 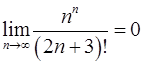 .
.
10.27.  . 10.28.
. 10.28.  .
.
10.29. 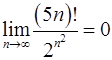 . 10.30.
. 10.30. 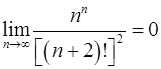 .
.
10.31. 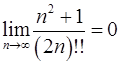 .
.
Задача 11.Найти область сходимости функционального ряда.
11.1. 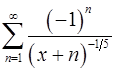 . 11.2.
. 11.2. 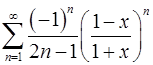 .
.
11.3. 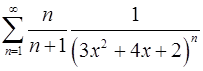 . 11.4.
. 11.4.  .
.
11.5. 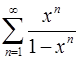 . 11.6.
. 11.6. 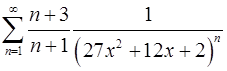 .
.
11.7. 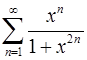 . 11.8.
. 11.8. 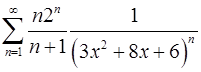 .
.
11.9. 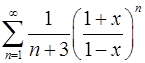 . 11.10.
. 11.10. 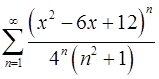 .
.
11.11.  . 11.12.
. 11.12.  .
.
11.13. 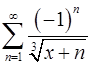 . 11.14.
. 11.14.  .
.
11.15. 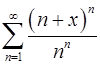 . 11.16.
. 11.16. 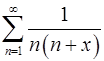 .
.
11.17. 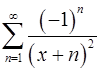 . 11.18.
. 11.18.  .
.
11.19. 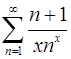 . 11.20.
. 11.20. 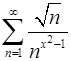 .
.
11.21.  . 11.22.
. 11.22. 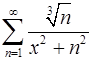 .
.
11.23. 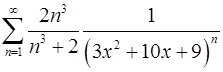 . 11.24.
. 11.24.  .
.
11.25. 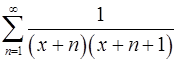 . 11.26.
. 11.26.  .
.
11.27.  . 11.28.
. 11.28.  .
.
11.29.  . 11.30.
. 11.30. 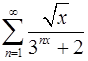 .
.
11.31. 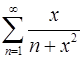 .
.
Задача 12.Найти область сходимости функционального ряда.
12.1. 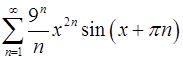 . 12.2.
. 12.2.  .
.
12.3. 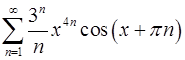 . 12.4.
. 12.4. 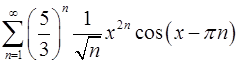 .
.
12.5.  . 12.6.
. 12.6. 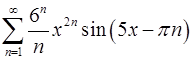 .
.
12.7. 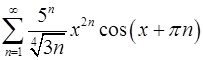 . 12.8.
. 12.8. 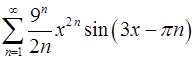 .
.
12.9.  . 12.10.
. 12.10.  .
.
12.11. 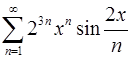 . 12.12.
. 12.12. 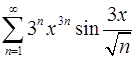 .
.
12.13. 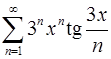 . 12.14.
. 12.14. 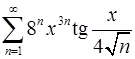 .
.
12.15.  . 12.16.
. 12.16. 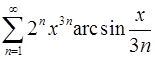 .
.
12.17.  . 12.18.
. 12.18.  .
.
12.19. 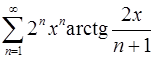 . 12.20.
. 12.20. 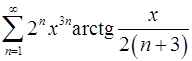 .
.
12.21.  . 12.22.
. 12.22. 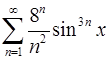 .
.
12.23. 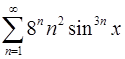 . 12.24.
. 12.24. 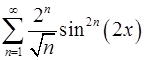 .
.
12.25.  . 12.26.
. 12.26. 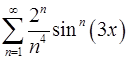 .
.
12.27. 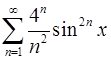 . 12.28.
. 12.28. 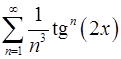 .
.
12.29. 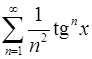 . 12.30.
. 12.30. 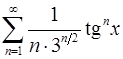 .
.
12.31. 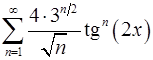 .
.
Задача 13.Найти область сходимости функционального ряда.
13.1.  . 13.2.
. 13.2. 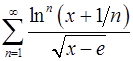 .
.
13.3.  . 13.4.
. 13.4. 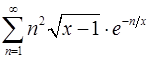 .
.
13.5.  . 13.6.
. 13.6. 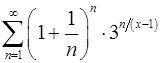 .
.
13.7. 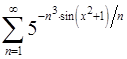 . 13.8.
. 13.8.  .
.
13.9. 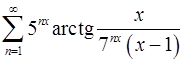 . 13.10.
. 13.10.  .
.
13.11. 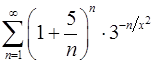 . 13.12.
. 13.12. 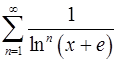 .
.
13.13. 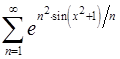 . 13.14.
. 13.14. 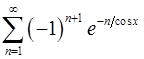 .
.
13.15. 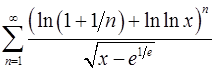 . 13.16.
. 13.16. 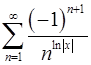 .
.
13.17. 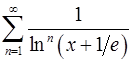 . 13.18.
. 13.18. 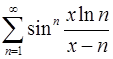 .
.
13.19. 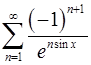 . 13.20.
. 13.20. 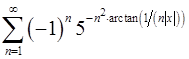 .
.
13.21.  . 13.22.
. 13.22.  .
.
13.23.  . 13.24.
. 13.24. 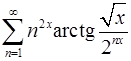 .
.
13.25.  . 13.26.
. 13.26. 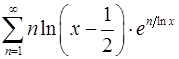 .
.
13.27.  . 13.28.
. 13.28. 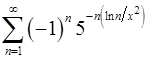 .
.
13.29. 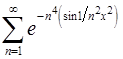 . 13.30.
. 13.30. 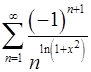 .
.
13.31.  .
.
Задача 14.Найти область сходимости функционального ряда.
14.1.  . 14.2.
. 14.2. 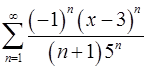 .
.
14.3. 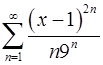 . 14.4.
. 14.4. 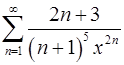 .
.
14.5. 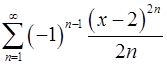 . 14.6.
. 14.6. 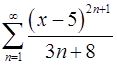 .
.
14.7. 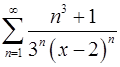 . 14.8.
. 14.8. 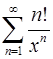 .
.
14.9. 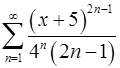 . 14.10.
. 14.10. 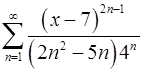 .
.
14.11. 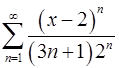 . 14.12.
. 14.12.  .
.
14.13. 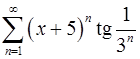 . 14.14.
. 14.14.  .
.
14.15. 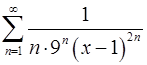 . 14.16.
. 14.16. 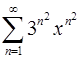 .
.
14.17. 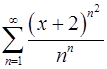 . 14.18.
. 14.18. 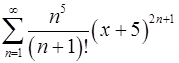 .
.
14.19.  . 14.20.
. 14.20. 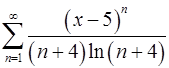 .
.
14.21.  . 14.22.
. 14.22. 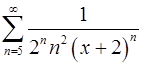 .
.
14.23.  . 14.24.
. 14.24.  .
.
14.25. 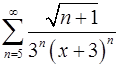 . 14.26.
. 14.26. 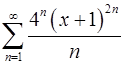 .
.
14.27.  . 14.28.
. 14.28. 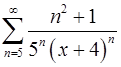 .
.
14.29. 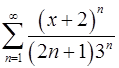 . 14.30.
. 14.30. 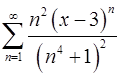 .
.
14.31.  .
.
Задача 15.Доказать, исходя из определения, равномерную сходимость функционального ряда на отрезке  . При каких
. При каких 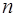 абсолютная величина остаточного члена ряда не превосходит
абсолютная величина остаточного члена ряда не превосходит 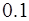
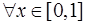 ?
?
15.1. 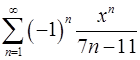 . 15.2.
. 15.2.  .
.
15.3. 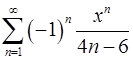 . 15.4.
. 15.4. 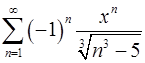 .
.
15.5. 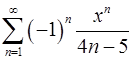 . 15.6.
. 15.6. 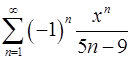 .
.
15.7. 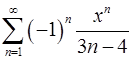 . 15.8.
. 15.8. 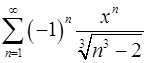 .
.
15.9. 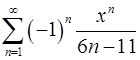 . 15.10.
. 15.10. 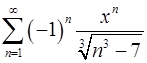 .
.
15.11. 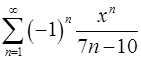 . 15.12.
. 15.12. 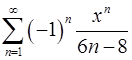 .
.
15.13. 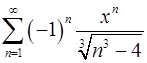 . 15.14.
. 15.14. 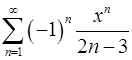 .
.
15.15.  . 15.16.
. 15.16.  .
.
15.17.  . 15.18.
. 15.18. 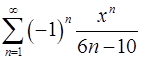 .
.
15.19. 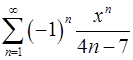 . 15.20.
. 15.20. 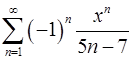 .
.
15.21. 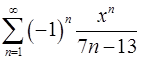 . 15.22.
. 15.22. 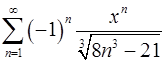 .
.
15.23. 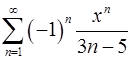 . 15.24.
. 15.24. 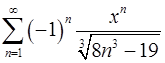 .
.
15.25.  . 15.26.
. 15.26. 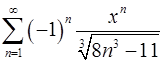 .
.
15.27. 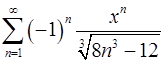 . 15.28.
. 15.28. 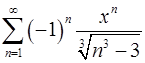 .
.
15.29. 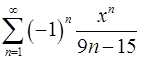 . 15.30.
. 15.30. 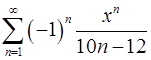 .
.
15.31. 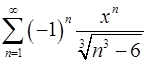 .
.
Задача 16.Для данного функционального ряда построить мажорирующий ряд и доказать равномерную сходимость на указанном отрезке.
16.1. 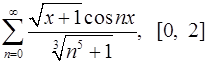 . 16.2.
. 16.2. 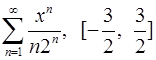 .
.
16.3.  . 16.4.
. 16.4. 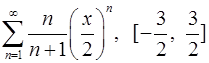 .
.
16.5. 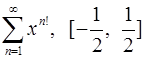 . 16.6.
. 16.6.  .
.
16.7.  . 16.8.
. 16.8.  .
.
16.9.  . 16.10.
. 16.10. 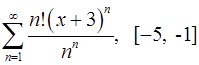 .
.
16.11. 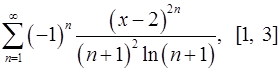 . 16.12.
. 16.12.  .
.
16.13.  . 16.14.
. 16.14. 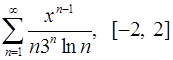 .
.
16.15. 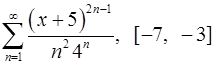 . 16.16.
. 16.16. 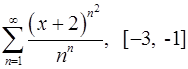 .
.
16.17. 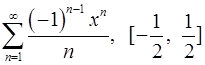 . 16.18.
. 16.18.  .
.
16.19.  . 16.20.
. 16.20. 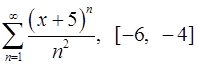 .
.
16.21. 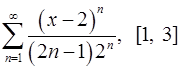 . 16.22.
. 16.22. 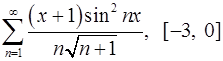 .
.
16.23. 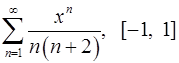 . 16.24.
. 16.24. 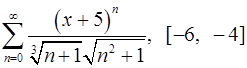 .
.
16.25. 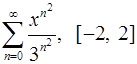 . 16.26.
. 16.26. 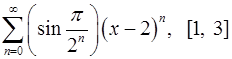 .
.
16.27. 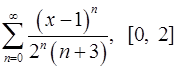 . 16.28.
. 16.28. 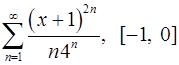 .
.
16.29. 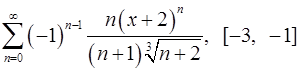 . 16.30.
. 16.30. 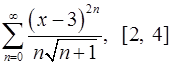 .
.
16.31. 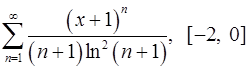 .
.
Задача 17. Найти сумму ряда.
17.1. 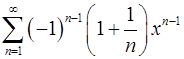 . 17.2.
. 17.2. 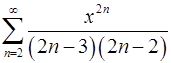 .
.
17.3. 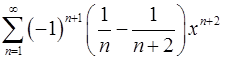 . 17.4.
. 17.4. 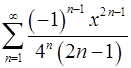 .
.
17.5. 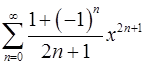 . 17.6.
. 17.6. 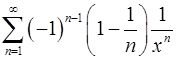 .
.
17.7. 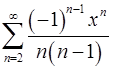 . 17.8.
. 17.8. 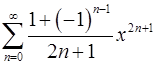 .
.
17.9.  . 17.10.
. 17.10. 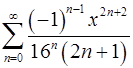 .
.
17.11. 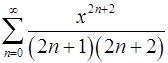 . 17.12.
. 17.12. 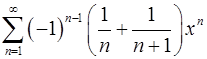 .
.
17.13. 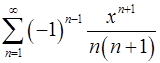 . 17.14.
. 17.14.  .
.
17.15. 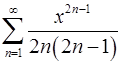 . 17.16.
. 17.16.  .
.
17.17.  . 17.18.
. 17.18. 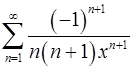 .
.
17.19. 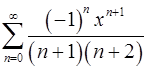 . 17.20.
. 17.20.  .
.
17.21. 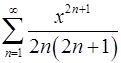 . 17.22.
. 17.22.  .
.
17.23. 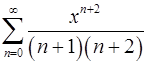 . 17.24.
. 17.24. 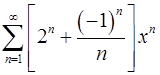 .
.
17.25. 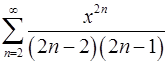 . 17.26.
. 17.26. 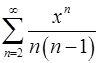 .
.
17.27.  . 17.28.
. 17.28.  .
.
17.29. 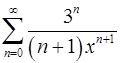 . 17.30.
. 17.30. 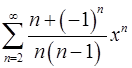 .
.
17.31. 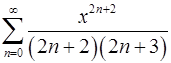 .
.
Задача 18. Найти сумму ряда.
18.1. 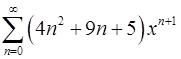 . 18.2.
. 18.2.  .
.
18.3. 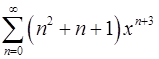 . 18.4.
. 18.4. 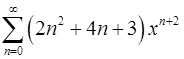 .
.
18.5. 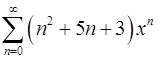 . 18.6.
. 18.6. 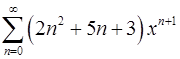 .
.
18.7. 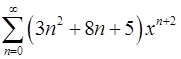 . 18.8.
. 18.8.  .
.
18.9. 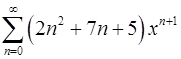 . 18.10.
. 18.10. 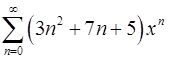 .
.
18.11. 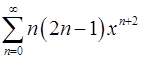 . 18.12.
. 18.12. 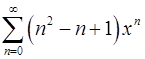 .
.
18.13.  . 18.14.
. 18.14. 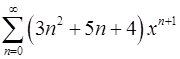 .
.
18.15. 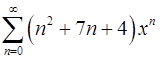 . 18.16.
. 18.16. 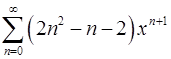 .
.
18.17. 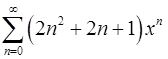 . 18.18.
. 18.18. 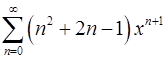 .
.
18.19. 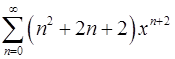 . 18.20.
. 18.20. 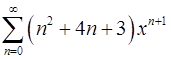 .
.
19.21.  . 18.22.
. 18.22. 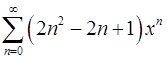 .
.
18.23.  . 18.24.
. 18.24. 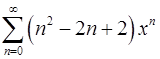 .
.
18.25.  . 18.26.
. 18.26. 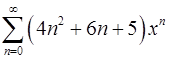 .
.
18.27. 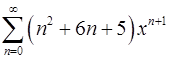 . 18.28.
. 18.28. 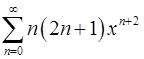 .
.
18.29. 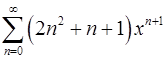 . 18.30.
. 18.30. 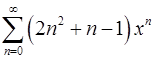 .
.
18.31.  .
.
Задача 19. Разложить функцию в ряд Тейлора по степеням 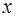 .
.
19.1.  . 19.2.
. 19.2. 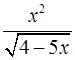 .
.
19.3. 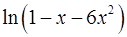 . 19.4.
. 19.4. 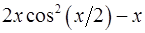 .
.
19.5.  . 19.6.
. 19.6. 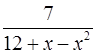 .
.
19.7.  . 19.8.
. 19.8. 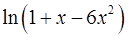 .
.
19.9. 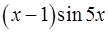 . 19.10.
. 19.10.  .
.
19.11. 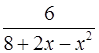 . 19.12.
. 19.12. 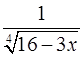 .
.
19.13.  . 19.14.
. 19.14. 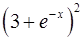 .
.
19.15. 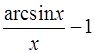 . 19.16.
. 19.16. 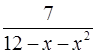 .
.
19.17.  . 19.18.
. 19.18. 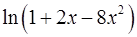 .
.
19.19. 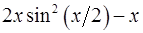 . 19.20.
. 19.20. 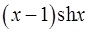 .
.
19.21. 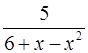 . 19.22.
. 19.22. 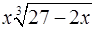 .
.
19.23.