Равномерная сходимость ряда Фурье

Сходимость ряда Фурье в точке

Пусть f (x) является кусочно гладкой функцией в интервале [−π, π]. Тогда для любого

где f (x₀ − 0) и f (x₀ + 0) представляют собой, соответственно, левосторонний и правосторонний пределы в точке x₀.

Равномерная сходимость ряда Фурье

Говорят, что последовательность частичных сумм ряда Фурье {f_N (x)} сходится равномерно к функции f (x), если скорость сходимости частичных сумм f_N (x) не зависит от x (рисунок 3). Будем говорить, что ряд Фурье функции f (x) сходится равномерно к этой функции, если

Теорема. Ряд Фурье 2π-периодической непрерывной и кусочно гладкой функции сходится равномерно.


Рис.3		Рис.4, n = 35

Сходимость ряда Фурье в пространстве L₂

Пространство L₂(−π, π) образовано функциями, удовлетворяющими условию

Будем говорить, что функция f (x) является квадратично интегрируемой, если она принадлежит классу L₂. Если f (x) квадратично интегрируема, то

то есть частичные суммы f_N (x) сходятся к f (x) в смысле среднего квадратичного.

Из равномерной сходимости ряда Фурье следует как сходимость в точке, так и сходимость в пространстве L₂. Обратное утверждение неверно: сходимость в пространстве L₂ не означает, что ряд Фурье сходится в точке или равномерно, и, аналогично, из сходимости в точке не вытекает равномерная сходимость или сходимость в пространстве L₂

Пусть функция 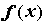абсолютно интегрируема на отрезке , то есть существует . Тогда ей можно поставить в соответствие ее тригонометрический ряд Фурье: . Коэффициенты тригонометрического ряда Фурье называют коэффициентами Фурье и вычисляют по формулам Эйлера-Фурье: 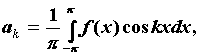. Если функция 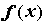кусочно-гладкая на отрезке , то ее тригонометрический ряд Фурье сходится в каждой точке этого отрезка. При этом, если - сумма ряда Фурье, то для любого . То есть, если 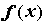непрерывна в точке 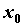, то 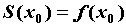. Если в точке 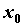у 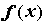разрыв первого рода, то ряд Фурье сходится к среднеарифметическому левого и правого пределов функции в точке .

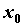ПРИМЕР 1. Разложение в ряд Фурье и исследование частичных сумм.

Разложение в ряд Фурье на произвольном отрезке. Для кусочно-гладкой на отрезке функции 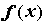задача о разложении в ряд Фурье на этом отрезке линейной заменой сводится к задаче о разложении функции на отрезке : , .