Простейшие тригонометрические уравнения.

1. Алгебраический метод. Этот метод нам хорошо известен из алгебры

( метод замены переменной и подстановки ).

2. Разложение на множители. Этот метод рассмотрим на примерах.

П р и м е р 1. Решить уравнение: sin x + cos x = 1 .

Р е ш е н и е . Перенесём все члены уравнения влево:

sin x + cos x – 1 = 0 ,

преобразуем и разложим на множители выражение в

левой части уравнения:

П р и м е р 2. Решить уравнение: cos ² x + sin x · cos x = 1.

Р е ш е н и е . cos ² x + sin x · cos x – sin ² x – cos ² x = 0 ,

sin x · cos x – sin ² x = 0 ,

sin x · ( cos x – sin x ) = 0 ,

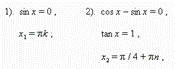
П р и м е р 3. Решить уравнение: cos 2x – cos 8x + cos 6x = 1.

Р е ш е н и е . cos 2x + cos 6x = 1 + cos 8x ,

2 cos 4x cos 2x = 2 cos ² 4x ,

cos 4x · ( cos 2x – cos 4x ) = 0 ,

cos 4x · 2 sin 3x · sin x = 0 ,

1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,

3.

Приведение к однородному уравнению. Уравнение называется однородным относительно sin и cos, если все его члены одной и той же степени относительно sin и cos одного и того же угла. Чтобы решить однородное уравнение, надо:   а) перенести все его члены в левую часть; б) вынести все общие множители за скобки; в) приравнять все множители и скобки нулю; г) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на cos ( или sin ) в старшей степени; д) решить полученное алгебраическое уравнение относительно tan .   П р и м е р . Решить уравнение: 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.   Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,   sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,   tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,   корни этого уравнения: y1 = -1, y2 = -3, отсюда 1) tan x = –1, 2) tan x = –3,

4. Переход к половинному углу. Рассмотрим этот метод на примере:

П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7.

Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =

= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,

2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,

tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,

. . . . . . . . . .

5. Введение вспомогательного угла. Рассмотрим уравнение вида:

a sin x + b cos x = c ,

где a, b, c – коэффициенты; x – неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно как cos 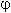и sin 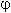( здесь 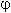- так называемый вспомогательный угол ), и наше уравнение принимает вид:

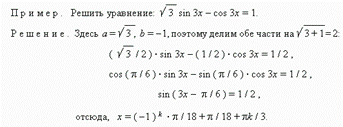
6. Преобразование произведения в сумму. Здесь используются соответствующие формулы.

П р и м е р . Решить уравнение: 2 sin x · sin 3x = cos 4x.

Р е ш е н и е . Преобразуем левую часть в сумму:

cos 4x – cos 8x = cos 4x ,

cos 8x = 0 ,

8x = p / 2 + pk ,

x = p / 16 + pk / 8 .

7. Универсальная подстановка. Рассмотрим этот метод на примере.

П р и м е р . Решить уравнение: 3 sin x – 4 cos x = 3 .

Таким образом, решение даёт только первый случай.

Областью значений функции y=cos x (см. рис. 2) является отрезок . На отрезке функция непрерывна и монотонно убывает.

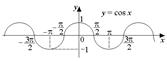
Рис. 2 Значит, на отрезке определена функция, обратная функции y=cos x. Эту обратную функцию называют арккосинусом и обозначают y=arccos x [2].

Определение

Aрккосинусом числа а, если |а| 1, называют угол, косинус которого принадлежит отрезку ; его обозначают arccos а.

Таким образом, arccos а есть угол, удовлетворяющий следующим двум условиям: сos (arccos a)=a, |а| 1; 0≤ arccos a ≤π.

Например, arccos , так как cos и ; arccos , так как cos и .

Функция y = arccos x (рис. 3) определена на отрезке , областью ее значений является отрезок . На отрезке функция y=arccos x непрерывна и монотонно убывает от π до 0 (поскольку y=cos х – непрерывная и монотонно убывающая функция на отрезке ); на концах отрезка она достигает своих экстремальных значений: arccos(–1)= π, arccos 1= 0.

Рассмотрим функцию y=sin х (рис. 6), которая на отрезке [–π/2;π/2] возрастающая, непрерывная и принимает значения из отрезка [–1; 1]. Значит, на отрезке [– π/2; π/2] определена функция, обратная функции y=sin x.

Рис. 6 Эту обратную функцию называют арксинусом и обозначают y=arcsin x. Введем определение арксинуса числа а [4].

Арксинусом числа а, если 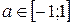называют угол (или дугу), синус которого равен числу а и который принадлежит отрезку [–π/2; π/2]; его обозначают arcsin а.

Таким образом, arcsin а есть угол, удовлетворяющий следующим условиям: sin (arcsin a)=a, |a| ≤1; –π/2 ≤ arcsin а ≤ π/2. Например, , так как sin и [– π/2; π/2]; arcsin , так как sin = и [– π/2; π/2].

Функция y=tg x на промежутке 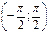принимает все числовые значения: E (tg x)= . На этом промежутке она непрерывна и монотонно возрастает. Значит, на промежутке определена функция, обратная функции y = tg x. Эту обратную функцию называют арктангенсом и обозначают y = arctg x [4].

Арктангенсом числа а называют угол из промежутка , тангенс которого равен а. Таким образом, arctg a есть угол, удовлетворяющий следующим условиям: tg (arctg a) = a и 0 ≤ arctg a ≤ π.

Функция y = ctg x на промежутке 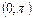принимает все числовые значения из промежутка . Область ее значений совпадает с множеством всех действительных чисел. В промежутке функция y = ctg x непрерывна и монотонно возрастает. Значит, на этом промежутке определена функция, обратная функции y = ctg x. Функцию, обратную котангенсу, называют арккотангенсом и обозначают y = arcctg x [4].

Арккотангенсом числа а называют угол, принадлежащий промежутку , котангенс которого равен а.

Таким образом, аrcctg a есть угол, удовлетворяющий следующим условиям: ctg (arcctg a)=a и 0 ≤ arcctg a ≤ π.