 |
|
Достаточные признаки сходимости положительных числовых рядов
Необходимый признак сходимости в общем случае не позволяет судить о том, сходится ли данный ряд или же нет. Сходимость ряда во многих случаях устанавливается с помощью так называемых достаточных признаков сходимости. Рассмотрим некоторые из этих признаков для частного вида рядов. В этом и следующем разделах будут рассматриваться ряды 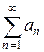 , все члены которых неотрицательны an≥ 0. Такие ряды называются положительными.
, все члены которых неотрицательны an≥ 0. Такие ряды называются положительными.
Исследованиесходимости (расходимости) положительного ряда удобно проводить путём сравнения его с другим («эталонным») рядом, о котором известно, сходится он или нет. В основе такого сравнения лежат следующие теоремы.
Теорема 1.Пусть даны два положительных ряда 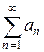 и
и  (an, bn ³ 0 )
(an, bn ³ 0 )
и выполняется неравенство an £ bn при любом n, тогда из сходимости ряда  следует сходимость ряда
следует сходимость ряда 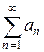 , а из расходимости ряда
, а из расходимости ряда 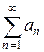 следует расходимость ряда
следует расходимость ряда .
.
Доказательство. Обозначим через Sn и sn частные суммы рядов 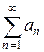 и
и  . Т.к. по условию теоремы ряд
. Т.к. по условию теоремы ряд  сходится, то его частные суммы ограничены, т.е. при всех n sn < M, где М – некоторое число. Но т.к. an £ bn, то Sn £ sn то частные суммы ряда
сходится, то его частные суммы ограничены, т.е. при всех n sn < M, где М – некоторое число. Но т.к. an £ bn, то Sn £ sn то частные суммы ряда 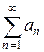 тоже ограничены, а этого достаточно для его сходимости. Второе утверждение теоремы доказывается методом от противного.
тоже ограничены, а этого достаточно для его сходимости. Второе утверждение теоремы доказывается методом от противного.
Пример 1. Исследовать на сходимость ряд 
Т.к.  , а гармонический ряд
, а гармонический ряд  расходится, то расходится и ряд
расходится, то расходится и ряд  .
.
Пример 2. Исследовать на сходимость ряд 
Т.к.  , а ряд
, а ряд  сходится ( как убывающая геометрическая прогрессия), то ряд
сходится ( как убывающая геометрическая прогрессия), то ряд  тоже сходится.
тоже сходится.
Теорема 2(предельный признак сравнения). Если для положительных рядов 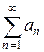 и
и  существует конечный и отличный от нуля предел
существует конечный и отличный от нуля предел  , то ряды
, то ряды 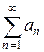 и
и  одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
На практике при применении теории сравнения часто в качестве «эталонных» рядов используются следующие ряды, сходимость (расходимость) которых известна:
1) расходящийся гармонический ряд  ;
;
2) обобщённый гармонический ряд  ;
;
3) геометрический ряд  .
.
Пример 1.Исследовать на сходимость ряд  .
.
Решение. Сравним данный ряд со сходящимся рядом  ,общими членами этих рядов являются
,общими членами этих рядов являются  и
и  . Применяем предельный признак сравнения
. Применяем предельный признак сравнения  . Ряд сходится.
. Ряд сходится.
Пример 2.Исследовать на сходимость ряд  .
.
Решение. Сравним данный ряд с расходящимся рядом  , применяем предельный признак сравнения
, применяем предельный признак сравнения  . Ряд расходится.
. Ряд расходится.
Пример 3.Исследовать на сходимость ряд  .
.
Решение. Сравним данный ряд с расходящимся рядом  , применяем предельный признак сравнения
, применяем предельный признак сравнения  . Ряд расходится.
. Ряд расходится.
Теорема 3.Пусть даны два положительных ряда 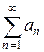 и
и  (an, bn ³ 0 )
(an, bn ³ 0 )
и выполняется неравенство  при любом n, тогда из сходимости ряда
при любом n, тогда из сходимости ряда  следует сходимость ряда
следует сходимость ряда 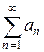 , а из расходимости ряда
, а из расходимости ряда 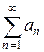 следует расходимость ряда
следует расходимость ряда .
.
Признак Даламбера
Пусть для положительного ряда 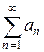 существует предел
существует предел  . Тогда ряд сходится при l < 1 и расходится при l >1.
. Тогда ряд сходится при l < 1 и расходится при l >1.
Доказательство. Пусть  , причём
, причём 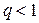 , тогда
, тогда 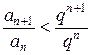 . Положим, что общий член сходящегося ряда
. Положим, что общий член сходящегося ряда 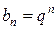 , т.е.
, т.е. 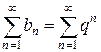 , тогда по теореме 3 из сходимости ряда
, тогда по теореме 3 из сходимости ряда  следует сходимость
следует сходимость 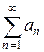 .
.
Если  , тогда
, тогда  , а это означает, что элементы ряда возрастают и по достаточному условию расходимости ряд расходится.
, а это означает, что элементы ряда возрастают и по достаточному условию расходимости ряд расходится.
Пример 1.Исследовать на сходимость ряд  .
.
Решение. По признаку Даламбера  . Ряд сходится.
. Ряд сходится.
Пример 2.Исследовать на сходимость ряд  .
.
Решение. По признаку Даламбера  . Ряд расходится.
. Ряд расходится.
Пример 3.Исследовать на сходимость ряд  .
.
Решение. По признаку Даламбера  . Ряд сходится.
. Ряд сходится.
Пример 4.Исследовать на сходимость ряд  .
.
Решение. По признаку Даламбера

=  . Ряд сходится.
. Ряд сходится.