 |
|
Знакопеременные ряды
Ряд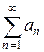 
называется знакопеременным, если он содержит бесконечное множество положительных и бесконечное множество отрицательных элементов.
Знакопеременный ряд 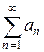называется абсолютносходящимся, если сходится ряд 
.
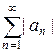Теорема(достаточный признак сходимости знакопеременного ряда). Если сходится ряд 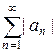, составленный из модулей членов ряда, то сходится и сам знакопеременный ряд .
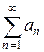Доказательство. Рассмотрим вспомогательный ряд 
. Очевидно, что 
для всех 
. Но ряд 
сходится, поэтому на основании признака сравнения сходится и ряд .Поскольку данный знакопеременный ряд представляет собой разность двух сходящихся рядов 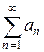= - 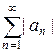, то он сходится.
Если ряд 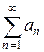сходится, а ряд 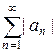, составленный из абсолютных величин, расходится, то говорят, что ряд 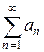сходится условно.
Рассмотрим важный класс рядов, называемых знакочередующимися. Знакочередующимся рядом называется ряд, для которого рядом стоящие члены имеют разные знаки, т.е.
.
Для знакочередующихся рядов имеет место достаточный признак сходимости Лейбница.
Теорема (признак Лейбница) Если для знакочередующегося ряда 
:
1) последовательность абсолютных величин членов ряда монотонно убывает, т.е. 
;
2) общий член ряда стремится к нулю 
, то ряд сходится.
Доказательство. Рассмотрим частичную сумму чётного числа (2m) членов ряда
.
Выражение в каждой скобке по первому условию теоремы положительно. Следовательно, сумма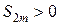 
. С другой стороны 
можно переписать в виде
.
Откуда видно, что 
. Таким образом, последовательность 
…,S2m,…возрастает и ограничена сверху. Следовательно, она имеет предел 
, причём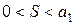 
.
Рассмотрим теперь частичные суммы нечётного числа (2m+1) членов ряда. Очевидно, что 
, поэтому
,
так как по второму условию теоремы 
. Итак 
при любом n (чётном или нечётном), т.е. ряд сходится, причём .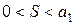
9.2. Функциональные ряды
Ряд называется функциональным, если его элементы являются функциями, которые определены на одном множестве Х
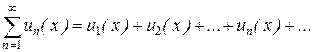(9.2)
При разных значениях х функциональный ряд становится числовым. Если при х = х0 
числовой ряд сходится, то точка х0 называется точкой сходимости; если же ряд расходится - точкой расходимости функционального ряда.
Множество числовых значений аргумента х , при которых функциональный ряд сходится, называется областью сходимости.
В области сходимости функционального ряда его сумма 
является функцией от аргумента х и она определяется как предел 
частичных сумм 
ряда (9.2).
Степенные ряды
Степенным рядомназывается ряд вида
. (9.3)
Рассмотрим теорему, имеющее важное значение в теории степенных рядов и касающаяся области сходимости степенного ряда.
Теорема Абеля. 1) Если степенной ряд (9.3) сходится при x = x0 , то он сходится и притом абсолютно для всех 
;
2) если степенной ряд (9.3) расходится при x = x1 , то он расходится для всех 
.
Доказательство. Так как числовой ряд 
сходится, то из необходимого условия сходимости общий член 
при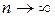 
, откуда следует, что последовательность { 
} ограничена, т.е. существует такое число М > 0, что | | < M , n = 0, 1, 2, …Перепишем ряд (9.3) в виде
и рассмотрим ряд, составленный из абсолютных величин его членов
(*)
Члены этого ряда в силу неравенства меньше членов ряда
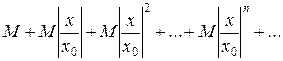
Данный ряд представляет собой сумму членов геометрической прогрессии со знаменателем 
и, следовательно, сходится. По признаку сравнения ряд (*) также сходится, а это значит, что при ряд (9.3) сходится абсолютно.
2) Докажем теперь вторую часть теоремы. По условию, в точке х1 ряд (9.3) расходится. Требуется показать, что он расходится для всех х, удовлетворяющих условию . Предположим обратное, т.е. допустим, что при некотором значении х таком, что , ряд (9.3) сходится. Тогда по только что доказанной первой части теоремы ряд (9.3) должен сходиться в точке х1, так как 
. Но это противоречит тому, что в точке х1 ряд расходится.
Интервал и радиус сходимости степенного ряда
Теорема Абеля утверждает, что если х0 – точка сходимости степенного ряда, то во всех точках, расположенных на интервале 
(рис 9.2а), этот сходится абсолютно, а если х1 – точка расходимости ряда, то во всех точках, расположенных вне интервала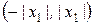 
(рис.9.2б), ряд расходится.
Рис. 9.2.
Интервал называют интервалом сходимости степенного ряда. Положив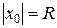 
, интервал сходимости можно записать в виде (-R, R). Число R называют радиусом сходимости степенного ряда, т.е. R > 0 – такое число, что при всех |х| < R, ряд (9.3) абсолютно сходится, а при |х| > R расходится. Отметим, что интервал сходимости для некоторых рядов охватывает всю числовую прямую (в этом случае 
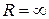), у других вырождается в одну точку ( 
). Таким образом, всякий степенной ряд имеет свой радиус сходимости R. При х = ± R ряд может либо сходиться, либо расходиться. Этот вопрос решается в каждом конкретном случае.
Можно показать, что из признака сходимости Даламбера радиус сходимости степенного ряда может быть определён соотношением 
.
Пример 1. Найти область сходимости ряда 
Решение. Находим радиус сходимости
.
Следовательно, данный ряд сходится при любом значении х. Общий член этого ряда стремится к нулю.
Пример 2. Найти область сходимости ряда 
Решение. Находим радиус сходимости 
.
Следовательно, ряд сходится при -2 < x + 2 < 2, т.е. при - 4 < х < 0. При х = -4 имеем ряд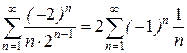 
, который по признаку Лейбница сходится. При х = 0 имеем расходящийся ряд 
.
Следовательно, областью сходимости исходного ряда является - 4 ≤ х < 0.
Пример 3.Ряд 
расходится на всей числовой прямой, кроме точки х = 0, так как радиус сходимости 
.