 |
|
Показательный закон распределения
Теорема сложения вероятностей
Теорема сложения вероятностей формулируется следующим образом.
Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:

Условная вероятность
Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.
Теорема умножения.
Теорема умножения. Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.
P(AB)=P(A)PA(B)
Независимые события
События А и В называются независимыми, если Р(АВ) = Р(А) Р(В). Несколько событий А, В, С,… называются независимыми, если вероятность их совместного осуществления равна произведению вероятностей осуществления каждого из них в отдельности: Р(АВС…) = Р(А)Р(В)Р(С)…
Формула полной вероятности. Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно,
 (формула Байеса).Пусть
(формула Байеса).Пусть  — полная группа событий, и — полная группа событий, и  — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие  , если в результате эксперимента наблюдалось событие , если в результате эксперимента наблюдалось событие  , может быть вычислена по формуле: , может быть вычислена по формуле:
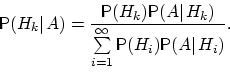 Формула Бернулли
Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < p < 1), событие наступит ровно k раз (безразлично, в какой последовательности), равна:
Pn(k)=Cnkpkqn-k
или
Формула Бернулли
Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < p < 1), событие наступит ровно k раз (безразлично, в какой последовательности), равна:
Pn(k)=Cnkpkqn-k
или

|
формула пуассона
Теорема. Если вероятность  наступления события
наступления события  в каждом испытании постоянна и мала, а число независимых испытаний
в каждом испытании постоянна и мала, а число независимых испытаний  достаточно велико, то вероятность наступления события
достаточно велико, то вероятность наступления события  ровно
ровно  раз приближенно равна
раз приближенно равна
 ,(3.4)
,(3.4)
где  .
.
Случайная величина
Случайной величинойназывается величина, которая в результате опыта может принимать то или иное значение, причем заранее известно какое именно. Это множество может быть как конечным, так и бесконечным.
Математические операции над случайными величинами
Прерывные случайные величины X и Y называются независимыми, если не зависимы при любых i и j, события X=xi и Y=yj.
Пусть случайная величина X принимает x1, x2, x3, …, xn с вероятностями p1, p2, p3 ,…, pn, соответственно, а Y-значения y1, y2, y3, …, ym, с вероятностями q1, q2, q3, …, qm.
а) Суммой случайных величин X и Y называется новая случайная величина Z=X+Y, которая принимает все значения вида zij=xi+yj(i=1,2,..n; j=1,2,...,m) с вероятностями pij, причем pij=P(X=xi; Y=yj)=P(X=xi)*PX=xi(Y=yj).
Если случайные величины X и Y независимые, то pij= pi+ qj.
Аналогично определяется разность и произведение случайных величин.
б) Разностью ( произведением) случайных величин X и Y называется новая случайная величина Z=X-Y (Z=XY), которая принимает все значения вида zij=xi-yj (zij=xiyj) с такими же вероятностями, с какими случайная величина Z=X+Y принимает соответствующие значения, т.е. pij= pi+ qj.
в) Произведением kX случайной величины Х на постоянную величину k называется новая случайная величина Z=kX, которая с теми же вероятностями, что и Х, принимает значения, равные произведениям значений случайной величины Х на k, т.е. =xi2.
г) Квадратом случайной величины Х, т.е. Х2, называется новая случайная величина Z=X2, которая с теми же вероятностями, что и Х, принимает значения, равные квадратам значений случайной величины Х, т.е. zi=xi2.
Математическим ожиданием дискретной случайной величины
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: M(X) = x1 p1+ x2 p2+...+ xn pn.
Реально на основе данных выборки мы не можем вычислить M(X). Однако эту характеристику можно оценить. В качествеоценки можно использовать среднее арифметическое, то есть M(X) ≈`X. Чем больше объём выборки (число наблюдений), тем точнее эта оценка. Математическое ожидание обладает следующими свойствами:
1. Математическое ожидание постоянной величины равно самой постоянной: M(C) = C.
2. Постоянный множитель можно выносить за знак математического ожидания: M(CX) = CM(X).
3. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых: M(X+Y+Z) = M(X)+M(Y)+M(Z).
4. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий: M(X×Y×Z) = M(X)×M(Y)×M(Z). Все эти свойства имеют большое практическое значение.
Дисперсией дискретной случайной величины
Дисперсией дискретной случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D ( X ) = M ( X - M ( X )) 2. Для вычислений удобнее пользоваться формулой :
D ( X ) = M ( X 2 ) - ( M ( X )) 2.
Дисперсия обладает следующими свойствами.
1. Дисперсия постоянной величины С равна нулю : D ( C ) = 0.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат : D ( CX ) = C 2D ( X ).
3. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин:
D ( X+Y+Z ) = D ( X )+D ( Y )+D ( Z ).
4. Дисперсия суммы постоянной величины и случайной - равна дисперсии случайной величины: D ( C+X ) = D ( X ).
Мода и медиана
Модой (Мо) случайной величины х называется наиболее вероятное ее значение. Это определение строго относится к дискретным случайным величинам. Для непрерывной величины модой называется такое ее значение для которого функция плотности распределения имеет максимальную величину.
Медианой (Ме)случайной величины называется такое ее значение для которого окажется ли случайная величина меньше этого значения. Для непрерывной случайной величины медиана это абсцисса точки в которой площадь под кривой распределяется пополам. Для дискретной случайной величины значение медианы зависит от того четное или нечетное значение случайной величины n=2k+1, то Ме=хк+1 (среднее по порядку значение) Если значение случайных величин четное, т.е n=2k, то Me=(xk+xk+1)/2
Биномиа́льное распределе́ние
Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из  независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них постоянна и равна
независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них постоянна и равна  .
.

Закон Пуассона
Закон Пуассона описывает вероятность возникновения n раз случайного события, имеющего интенсивность λ, за промежуток времени τ:
Pn(τ) = (λ∙τ)n/(n!) ∙ exp(-λ∙τ)
Характерные свойства закона Пуассона:
- математическое ожидание числа событий за промежуток времени τ равно λ∙τ: mx=λ∙τ;
- дисперсия числа событий – σ2=λ∙τ;
- распределение несимметричное, несимметричность особенно выражена при малых λ∙τ.
Геометри́ческое распределе́ние
Геометри́ческое распределе́ние в теории вероятностей — распределение дискретной случайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успеха». 
Показательный закон распределения
Теорема:Математическое ожидание и среднеквадратическое отклонение случайной величины, распределенной по показательному закону с параметром  , равны:
, равны:
 .
.