 |
|
Теорема 1: (неравенство Чебышева)
Для любой СВ Х, имеющей МО и дисперсию, справедливо неравенство 
Доказательство:Введем в рассмотрение новую СВ: Y=[X-M(X)]  так как СВ Y>=0, то по Лемме Чебышева получаем:
так как СВ Y>=0, то по Лемме Чебышева получаем:  или, что тоже самое:
или, что тоже самое:  с другой стороны
с другой стороны 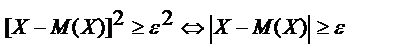
 тогда неравенство (*) примет вид:
тогда неравенство (*) примет вид:

Следствие:Поскольку события  противоположны, то неравенства Чебышева можно записать в виде:
противоположны, то неравенства Чебышева можно записать в виде:

Теорема 2: (теорема Чебышева) Если СВ  попарно независимы и
попарно независимы и  где С – некоторая постоянная, то при любом
где С – некоторая постоянная, то при любом  справедливо равенство:
справедливо равенство:

Доказательство:Введем в рассмотрение новую СВ  найдем МО и оценку дисперсии СВ Х:
найдем МО и оценку дисперсии СВ Х:
Запишем неравенство Чебышева в формуле (1) для СВ Х:
Зам: (смысл теоремы Чебышева): При большом числе n СВ  практически достоверно, что их средняя
практически достоверно, что их средняя  хотя есть величина случайная, но она сколь угодно мало отличается от неслучайной величины
хотя есть величина случайная, но она сколь угодно мало отличается от неслучайной величины  , то есть практически перестает быть случайной.
, то есть практически перестает быть случайной.
Зам!: т. Ч-ва является наиболее общим законом больших чисел, а теорема Бернулли, рассматр-ая ниже, простейшим.
Т3: (теорема Бернулли): Пусть  число успехов в n испытаниях Бернулли и р - вероятность появления успеха в каждом испытании, тогда при любом числе
число успехов в n испытаниях Бернулли и р - вероятность появления успеха в каждом испытании, тогда при любом числе  справедливо равенство:
справедливо равенство:

Доказательство:Воспользуемся след. представлением для СВ  :
:  , где
, где  - это ДСВ, означающая число появления успеха в i-ом испытании (i=1,2,3,….,n). Т. к. испытания Бернулли повторны и независимы, то СВ
- это ДСВ, означающая число появления успеха в i-ом испытании (i=1,2,3,….,n). Т. к. испытания Бернулли повторны и независимы, то СВ  (i=1,2,,….,n) будут попарно независимы и одинаково распределены, то есть будут иметь одинаковый ряд распределения.
(i=1,2,,….,n) будут попарно независимы и одинаково распределены, то есть будут иметь одинаковый ряд распределения.
Т.о. дисперсии СВ  (i=1,2,…,n) ограничены одной величиной, а значит к этим CD можно применить т. Ч-ва.
(i=1,2,…,n) ограничены одной величиной, а значит к этим CD можно применить т. Ч-ва.
Центральная, предельная теорема.
Теорема 4: (центральная, предельная теорема).
Если 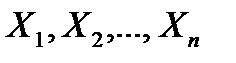 независимые СВ, имеющие одно и тоже распределение с МО и дисперсией
независимые СВ, имеющие одно и тоже распределение с МО и дисперсией 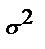 , то при неограниченном возрастании n, закон распределения суммы Х=
, то при неограниченном возрастании n, закон распределения суммы Х=  , неограниченно приближается к нормальному.
, неограниченно приближается к нормальному.