 |
|
Дисперсия, её свойства.
Практика показывает, что для более полного описания случайной величины необходимо ввести еще меру рассеивания, разброса значений, принимаемых случайной величиной Х, вокруг её математического ожидания. Введем полезное в дальнейшем понятие.
Определение. Случайная величина 
называется центрированной случайной величиной (флюктуацией).
Основными характеристиками разброса случайной величины относительно среднего значения служат дисперсия и среднее квадратичное отклонение.
Определение. Дисперсией D(X) (рассеянием) случайной величины Х называется математическое ожидание квадрата её флюктуации:
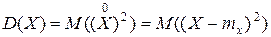(6)
Для дискретной случайной величины Х имеем по определению:
(7)
Для непрерывной случайной величины дисперсия выражается формулой:
.
Из формулы (7) видно, что физическим аналогом дисперсии случайной величины является центральный момент инерции стержня, на котором распределена (дискретно или непрерывно с плотностью равной f(x) ) единичная масса. Чем меньше разброс массы вокруг центра тяжести стержня, тем меньше момент инерции стержня.
Рассмотрим свойства дисперсии.
1)Дисперсия случайной величины неотрицательна.
2)Дисперсия случайной величины Х равна разности среднего значения квадрата случайной величины и квадрата её среднего значения:
. (8)
3)Дисперсия постоянной величины равна нулю.
4)Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
(9)
5)Для любых случайных величин X,Y
(10)
Таким образом, дисперсия суммы независимых случайных величин равна сумме их дисперсий. Отметим, что дисперсия разности двух независимых случайных величин также равна сумме их дисперсий.
Размерность дисперсии равна квадрату размерности случайной величины. Если нужно получить оценку рассеивания случайной величины в тех же единицах, то используют среднеквадратическое отклонение.
Определение. Среднеквадратическим отклонением σ(X) случайной величины Х называется корень квадратный из её дисперсии:
(12)