 |
|
ІСНУВАННЯ КОРЕНІВ, ЩО ЗАДОВОЛЬНЯЮТЬ ПЕВНІ УМОВИ
Нехай  і
і  – корені рівняння
– корені рівняння  , де
, де 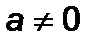 ;
; 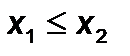 ,
,  ,
, 
 – абсциса вершини параболи
– абсциса вершини параболи  .
.
Тоді мають місце такі твердження:
ü 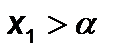 , якщо виконуються умови:
, якщо виконуються умови:

ü  , якщо виконуються умови:
, якщо виконуються умови:


ü  , якщо виконуються умови:
, якщо виконуються умови:

ü  , якщо виконуються умови:
, якщо виконуються умови:
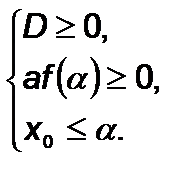

ü  , якщо виконуються умова
, якщо виконуються умова  .
.

ü  , якщо виконуються умови:
, якщо виконуються умови:


ü  ,
,  якщо виконуються умови:
якщо виконуються умови:
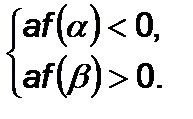

ü  ,
,  якщо виконуються умови:
якщо виконуються умови:

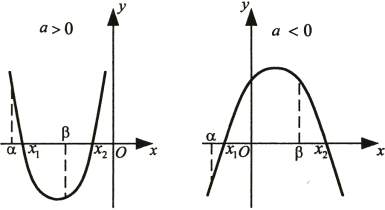
ü 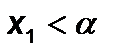 ,
,  якщо виконуються умови:
якщо виконуються умови:


Приклад 1.Розв’язати квадратне рівняння 
Розв’язування: якщо  , дане рівняння перетворюється в лінійне рівняння:
, дане рівняння перетворюється в лінійне рівняння:  ,
,  . Звідки
. Звідки  .
.
Якщо  , то дане рівняння є квадратним. Знайдемо дискримінант:
, то дане рівняння є квадратним. Знайдемо дискримінант:

 , якщо
, якщо 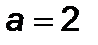 . Тоді дане рівняння набирає вигляду:
. Тоді дане рівняння набирає вигляду:  .
. 
 .
. 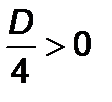 , якщо
, якщо  . Дане рівняння має два корені:
. Дане рівняння має два корені:  ,
,  ,
, 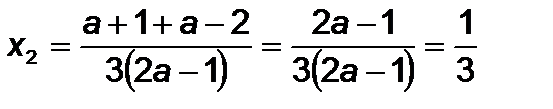 .
.
Відповідь.Якщо  ,
, 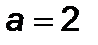 , то
, то  ; якщо
; якщо  ,
,  , то
, то  ,
, 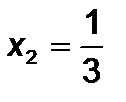 .
.
Приклад 2.Розв’язати квадратне рівняння 
Розв’язування: ОДЗ:  . На цьому ОДЗ дане рівняння рівносильне такому:
. На цьому ОДЗ дане рівняння рівносильне такому:  .
.

 , якщо
, якщо 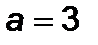 . Тоді
. Тоді  ,
, 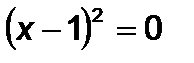 ,
,  – сторонній корінь, оскільки
– сторонній корінь, оскільки  не входить в ОДЗ – рівняння не має коренів.
не входить в ОДЗ – рівняння не має коренів.
 , якщо
, якщо  .
.
Дане рівняння має два корені:
 ,
,
 – сторонній корінь,
– сторонній корінь,
 .
.
Підставимо значення  в нерівність
в нерівність  :
:  ,
,  .
.
Відповідь.Якщо  , то рівняння не має коренів; якщо
, то рівняння не має коренів; якщо  , то рівняння має єдиний корінь
, то рівняння має єдиний корінь  .
.
Приклад 3.Розв’язати квадратне рівняння 
Розв’язування: ОДЗ:  . На цьому ОДЗ дане рівняння рівносильне такому:
. На цьому ОДЗ дане рівняння рівносильне такому:  .
.  ,
,  , якщо
, якщо  .
.

Якщо  , то
, то  ,
,
 ,
,
 .
.
Якщо  , то
, то  ,
,
 ,
,
 .
.
 , якщо
, якщо  – рівняння не має розв’язків.
– рівняння не має розв’язків.
 , якщо
, якщо  . Тоді
. Тоді  ,
,  ,
, 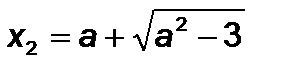 .
.
Підставимо значення  та
та  у нерівність
у нерівність  :
:
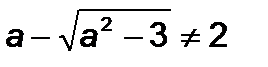 ,
,
 ,
,
 ,
,
 ,
,
 ,
,  .
.
У випадку 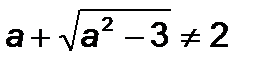 також одержуємо
також одержуємо 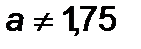 .
.
Якщо  ,
,  ,
,  ,
,  .
.
Відповідь.Якщо  , рівняння не має розв’язків;
, рівняння не має розв’язків;
якщо  , то
, то  ;
;
якщо  , то
, то  ;
;
якщо  , то
, то  ;
;
якщо  , то рівняння має 2 корені:
, то рівняння має 2 корені: 
Приклад 4.При скількох цілих значеннях параметра 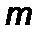 квадратне рівняння
квадратне рівняння  не має дійсних коренів?
не має дійсних коренів?
Розв’язування: дискримінант рівняння 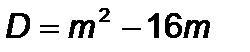 . Рівняння не має дійсних коренів, якщо
. Рівняння не має дійсних коренів, якщо  , тобто
, тобто  .
.
Використовуючи метод інтервалів розв’язування нерівностей, маємо  ,
,  .
.
Цілі значення з цього проміжку такі: 1, 2, 3, …, 15.
Відповідь. 15.
Приклад 5.При якому значенні параметра а рівняння  має єдиний розв’язок?
має єдиний розв’язок?
Розв’язування розкривши дужки та звівши подібні доданки, дістанемо:
 .
.
Останнє рівняння має єдиний розв’язок, якщо його дискримінант дорівнює нулю, тобто  , звідки
, звідки  . Тоді
. Тоді  .
.
Відповідь.  .
.
Приклад 6.Обчислити суму цілих значень параметра  , при яких рівняння
, при яких рівняння  має два різні дійсні корені.
має два різні дійсні корені.
Розв’язування: дане рівняння є квадратним, якщо  , тобто
, тобто  , і має два дійсні корені, якщо
, і має два дійсні корені, якщо  .
. 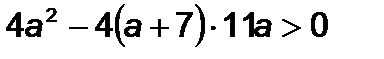 ;звідси
;звідси  ,або
,або  ,
,  .
.
Сума цілих значень параметра  .
.
Відповідь.  .
.