 |
|
Розв’язування квадратних нерівностей з параметрами
Під час розв’язування квадратичних нерівностей можна використовувати як метод інтервалів, так і графік квадратичної функції.
Квадратичною нерівністю з параметрами називають, наприклад, нерівність виду  , де
, де  – невідоме, а
– невідоме, а  ,
, 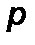 ,
,  – вирази, що залежать тільки від параметрів, причому
– вирази, що залежать тільки від параметрів, причому 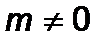 .
.
Якщо, наприклад, треба розв’язати нерівність  і в умові задачі не конкретизують, що це квадратна нерівність, то обов’язково треба розглянути випадок, коли
і в умові задачі не конкретизують, що це квадратна нерівність, то обов’язково треба розглянути випадок, коли  , та розв’язати лінійну нерівність.
, та розв’язати лінійну нерівність.
Використовуючи графік квадратичної функції, квадратичну нерівність  можна розв’язати так.
можна розв’язати так.
1) Якщо  , то
, то  .
.
2) Якщо  , то розглянемо функцію
, то розглянемо функцію 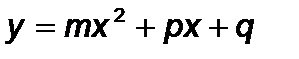 та побудуємо схематично її графік залежно від значення
та побудуємо схематично її графік залежно від значення  .
.
а) Нехай  .Якщо
.Якщо  , то
, то 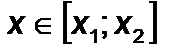 , де
, де  ,
,  – корені квадратного тричлена.
– корені квадратного тричлена.

Якщо  , то
, то  .
.

Якщо 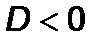 , то
, то  .
.
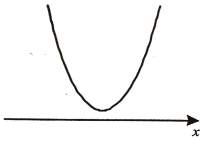
б) Нехай 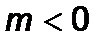 . Якщо
. Якщо  , то
, то  , де
, де  ,
,  – корені квадратного тричлена.
– корені квадратного тричлена.

Якщо  , то
, то  .
.

Якщо 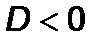 , то
, то  .
.
Приклад 1.Розв’язати нерівність  .
.
Розв’язування: знайдемо дискримінант лівої частини нерівності: 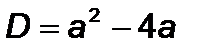 .
.  , коли
, коли 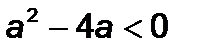 .Якщо
.Якщо  ,
,  .
.  , коли
, коли  ,
,  ,
,  .Якщо
.Якщо  ,
,  . Якщо
. Якщо  ,
,  ,
,  .
.  , коли
, коли 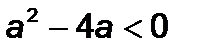 ,
, 
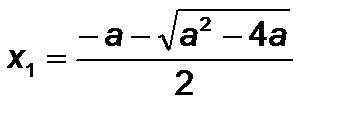 ,
, 
 .
.
Відповідь. Якщо  , то
, то  ; якщо
; якщо  , то
, то  ; якщо
; якщо  , то
, то  ; якщо
; якщо  , то
, то  .
.
Приклад 2.Знайти всі значення параметра  , при яких нерівність
, при яких нерівність 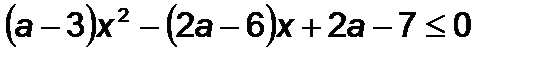 виконується для всіх дійсних значень
виконується для всіх дійсних значень  .
.
Розв’язування: знайдемо дискримінант лівої частини нерівності:
 .
.
Квадратична функція лівої частини нерівності набирає недодатних значень за умови 
Звідки


Відповідь.  .
.
Приклад 3.Знайти всі значення параметра  , при яких функція
, при яких функція
 визначена для всіх дійсних значень
визначена для всіх дійсних значень  .
.
Розв’язування: необхідно знайти всі значення  , при яких нерівність
, при яких нерівність
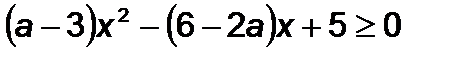 виконується для всіх
виконується для всіх  .
.
 .
.
Умові задачі відповідає система

Тоді


Відповідь.  .
.
 Приклад 4.Розв’язати нерівність
Приклад 4.Розв’язати нерівність  .
.
Розв’язування: оскільки  для всіх
для всіх 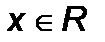 , то нерівність рівносильна системі:
, то нерівність рівносильна системі: 

Виконаємо графічну ілюстрацію в системі  .
.
Відповідь. Якщо  , то
, то  ; якщо
; якщо  , то
, то  ; якщо
; якщо  , то
, то  ; якщо
; якщо  , то
, то 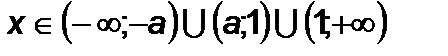 ; якщо
; якщо  , то
, то  ; якщо
; якщо  , то
, то  .
.