Свойства математического ожидания

1.Математическое ожидание постоянной величины равно самой постоянной:
.
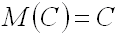2.Постоянный множитель можно вынести за знак математического ожидания:
.
3.Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
.
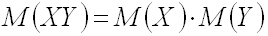Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.
4.Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:
.

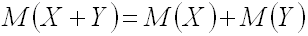Вопрос

Дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величиной от ее математического ожидания:
.

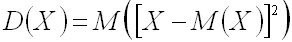Свойства дисперсии

1.Дисперсия постоянной величины равно нулю:
.
2.Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
.
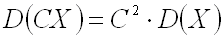3.Дисперсия суммы двух независимых случайных величин равно сумме дисперсий этих случайных величин:
.
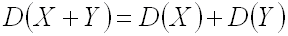Следствие. Дисперсия суммы нескольких взаимно независимых случайных величин равно сумме дисперсий этих величин.
4.Дисперсия разности двух независимых случайных величин равно сумме дисперсий этих случайных величин:
.

Вопрос

Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:
.
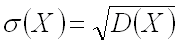Размерность среднего квадратического отклонения совпадает с размерностью самой случайной величины.

Вопрос

Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них постоянна и равна .

Биноминальное распределение - это распределение вероятностей возможных чисел появления события А при n независимых испытаниях, в каждом из которых событие А может осуществиться с одной и той же вероятностью Р(А) = р = const. Кроме события А может произойти также противоположное событие Ā, вероятность которого Р(Ā) = 1 - р = q.

Вероятности любого числа событий соответствуют членам разложения бинома Ньютона в степени, равной числу испытаний:

где pⁿ^-вероятность того, что при n испытаниях событие А наступит n раз;

qⁿ - вероятность того, что при n испытаниях событие А не наступит ни разу;

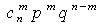- вероятность того, что при n испытаниях событие А наступит m раз, а событие Āнаступит n-m раз;

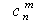-число сочетаний (комбинаций) появления события А и Ā.

Числовые характеристики биноминального распределения:

М(m)=np - математическое ожидание частоты появления события А при n независимых испытаниях;

D(m)=npq - дисперсия частоты появления события. А;

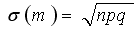- среднее квадратическое отклонение частоты.

Вопрос

Геометрическое распределение в теории вероятностей — распределение дискретной случайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успеха».

Пусть 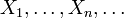— бесконечная последовательность независимых случайных величин с распределением Бернулли, то есть

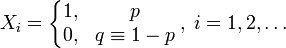
Построим случайную величину 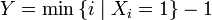— количество «неудач» до первого «успеха». Распределение случайной величины называется геометрическим с вероятностью «успеха» , что обозначается следующим образом: .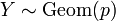

Функция вероятности случайной величины имеет вид:

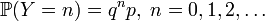
Вопрос

Функцией распределения вероятностей называют функцию 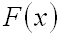, определяющую вероятность того, что случайная величина 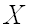в результате испытания примет значение, меньшее , то есть:
.
Случайную величину называют непрерывной, если ее функция распределения вероятностей есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

Вопрос

Непреры́вное равноме́рное распределе́ние — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины.

Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезк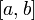е , где 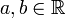, если её плотность имеет вид:

Пишут: 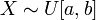. Иногда значения плотности в граничных точках и меняют на другие, например 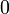или 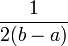. Так как интеграл Лебега от плотности не зависит от поведения последней на множествах меры нуль, эти вариации не влияют на вычисления связанных с этим распределением вероятностей.

Вопрос

Плотность вероятности — один из способов задания вероятностной меры на евклидовом пространстве 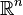. В случае, когда вероятностная мера является распределением случайной величины, говорят о плотности случайной величины. Пусть является вероятностной мерой на 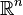, то есть определено вероятностное пространство 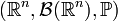, где 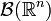обозначает борелевскую σ-алгебру на 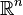. Пусть 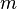обозначает меру Лебега на .

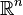Определение 1. Вероятность называется абсолютно непрерывной (относительно меры Лебега) ( 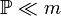), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:

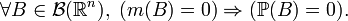
Если вероятность абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция 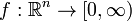такая, что

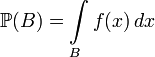где использовано общепринятое сокращение 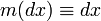, и интеграл понимается в смысле Лебега.

Определение 2. В более общем виде, пусть 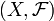— произвольное измеримое пространство, а 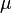и — две меры на этом пространстве. Если найдется неотрицательная 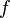, позволяющая выразить меру через меру 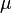в виде

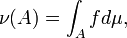
то такую функцию называют плотностью меры по мере 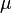, или производной Радона-Никодима меры относительно меры 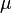, и обозначают

Вопрос

Функция распределения в теории вероятностей — функция, характеризующая распределение случайной величины или случайного вектора. При соблюдении известных условий (см. ниже) полностью определяет случайную величину. Пусть дано вероятностное пространство 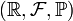, и на нём определена случайная величина 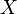с распределением . Тогда функцией распределения случайной величины 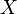называется функция 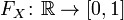, задаваемая формулой:

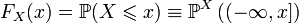То есть функцией распределения (вероятностей) случайной величины 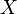называют функцию 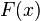, значение которой в точке 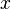равно вероятности события , то есть события, состоящего только из тех элементарных исходов, для которых .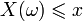

Вопрос

12 Следующая ⇒